Dimensionality reduction with SVD
How does SVD reduce the dimension of data?
Singular Value Decomposition by itself produces an exact fit. But you can use the decomposed form to find a lower-rank matrix which approximates the original matrix.
Given the decomposition A=UDV* (where U and V are unitary matrices), D is a diagonal matrix whose entries are the “singular values” of A, and has the same rank as A. But if we truncate D to contain just the largest k values on its diagonal, that is the best approximation of A that has rank k (according to a least-squares goodness of fit.)
Thus, SVD followed by elimination of some singular values reduces the dimension, but this is often just referred to as “SVD” in context.
An Example
Many machine learning toolkits include SVD, but we can use Wolfram Alpha to show a simple example. Given the input matrix
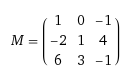
its SVD is
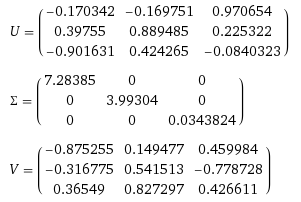
If we zero the lowest value in the diagonal matrix Σ and multiply back out (remember to transpose V!) we get

You can eyeball this and see it's pretty close to the original value M, but it only has rank 2 instead of rank 3 (though since we proceeded numerically, Wolfram Alpha would give a small but nonzero determinant for the result.) Dropping the dimension all the way down to one by eliminating another of the singular values gives us:

which is a pretty crude approximation, but it is the best single-dimensional (rank 1) approximation of the original matrix that we can make.
Originally answered on Quora (without the example): https://www.quora.com/How-is-SVD-reducing-the-data-dimension-We-are-taking-one-matrix-and-splitting-it-into-three-after-all/answer/Mark-Gritter
Congratulations @markgritter! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard!
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
I wish I understood better exactly what SVD does. I've used it many times, and it works great, but I'm a math user, not a real mathematician. The two applications where I've found it helpful is when fitting an over determined set of equations and PCA.
The funny thing is that PCA makes complete sense to me when I'm thinking in terms of diagonalizing a covariance matrix to find the eigenvalue and vectors, but the SVD approach to PCA is still a black box to me.
I have to admit that my mathematics background is almost entirely in abstract algebra, so I have to work hard on numerical methods and linear-algebra based ML techniques. :)
I minored in Math and thought Abstract Algebra was absolutely fantastic! It was like learning a whole new way of thinking. My professor at the time (1999) taught by having the homework due the day before the lecture. His claim was that it generated questions during class. I very much enjoyed this approach, although at times it was very frustrating.
At this point the only aspects of Abstract Algebra that I still use is group theory as it applies to symmetry in quantum mechanics, and even then, this is already worked out so it is just applying the established irreducible representations. (OK... to be more honest, I haven't been active in the lab in years, but this is because I spend my time working with my graduate students and writing proposals to support them.)