Asymptotic Bounds You May Not Have Learned In School
Computer Science education teaches "Big O" notation for describing complexity upper bounds, and Big-Theta and Big-Omega get introduced as well. Mathematicians and complexity theorists sometimes use "little o" as a stronger description of asymptotic behavior. But here are some bounds you may not have learned.
Big-D notation
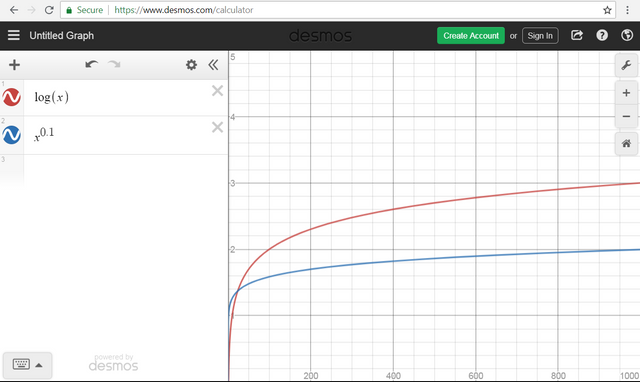
f(x) is D(g(x)) if you plot the two on Desmos, and it looks like f(x) < g(x).
Example: n^r is D( log(n) ) for small values of r, even though log(n) is O(n^r)for any positive r.
This notation is surprisingly popular with many students, perhaps due to trouble distinguishing a handwritten 'O' from a handwritten 'D'. Unfortunately, the broader mathematical community is resistant to this innovation in asymptotic analysis.
little-w asymptotic bound
f(x) is w(g(x)) if you hand-wave hard enough that the two are equivalent.
Example: 2^(n/2) is w(2^n), because all running times that use an exponent are the same.
This notation frequently gets used in the context of NP-complete problems where it asserted that the best known running time is w(2^n). (Upper bounds on 3SAT are actually as low as O(1.321^n) for a randomized algorithm.)
curly-O notation
The curly-O notation is the same as big-O, but reserved for those who want to show off their typesetting or calligraphy skills.
Example:
QWT-boundedness
A decision function that could be computed in time f(n) on a quantum computer because it "explores all universes simultaneously" is QWT(f(n))
(Editor's note: that's not how quantum computers work.)
Πnotation
A randomized procedure's run time is Œ( g(x) ) if the bound on its expected run time is O(g(x)), or if the function is described in Old English.
Example: lookup in a hash table takes Œ(1) time. It does not take O(1) time as sloppy writing sometimes indicates.
Example: the notorious Beowulf reduction demonstrates the complexity class M_onsters are all Œ(Geats). "Hwæt. We Gardena in geardagum, þeodcyninga, þrym gefrunon, hu ða æþelingas ellen fremedon...."
Shrug relation
f(x) ¯\_(ツ)_/¯ g(x) if either f(x) is asymptotically less than g(x), or g(x) is asymptotically less than f(x), but we're not sure which, or the proof is too complicated to explain.
Example: The Slow-growing hierarchy g_α(n) eventually catches up with the Fast-growing hierarchy f_α(n), so f_α(n) ¯\_(ツ)_/¯ g_α(n) because who understands infinite ordinals anyway.
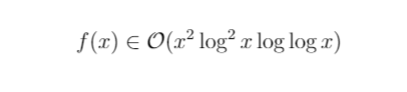
Congratulations @markgritter! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
You had me chuckling :)
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @markgritter!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV