Hello friends of steemit continuing with my explanations about the science of mathematics, today I want to make reference to the series of taylor, which is a very important series since it allows to obtain an approximation of functions through a series of powers, in this post establishes the definition, the history and also explains each of the functions that are related to the Taylor series.

Taylor series

In mathematics, a series of Taylor is an approximation of functions by a series of powers or sum of whole powers of polynomials such as (xa) ^ n called terms of the series, said sum is calculated from the derivatives of the function for a a certain value or point a sufficiently derivable on the function and an environment on which the series converges. The series centered on the zero point, a = 0, is also called the McLaurin series.

This approach has three important advantages:

• the derivation and integration of one of these series can be carried out term by term, which are trivial operations;
• it can be used to calculate approximate values ​​of functions;
• it is possible to calculate the optimality of the approach.
  Some functions can not be written as Taylor series because they have some singularity. In these cases a serial development can usually be achieved using negative powers of x (see Laurent's Series). For example f (x) = exp (-1 / x²) can be developed as a Laurent series.

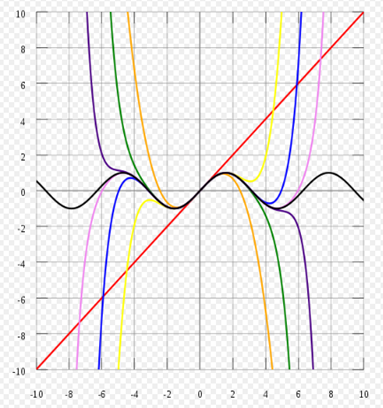
As the degree of the MacLaurin polynomial increases, it approaches function. The approximations of MacLaurin to sin (x), centered on 0, of degrees 1, 3, 5, 7, 9, 11 and 13 are illustrated.

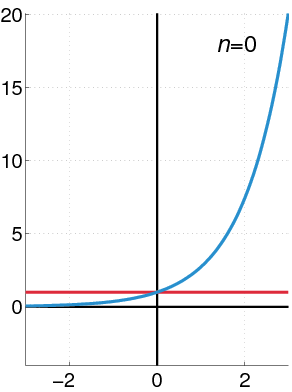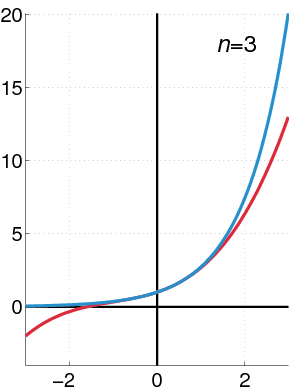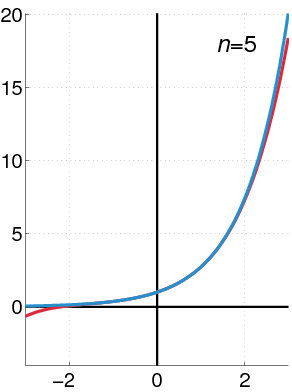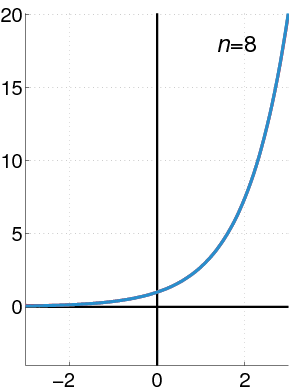
The graph of the exponential function (in blue), and the sum of the first n + 1 terms of its Taylor series around zero (in red).

Definition

The Taylor series of a real or complex function f (x) infinitely differentiable in the environment of a real or complex number a is the following series of powers:

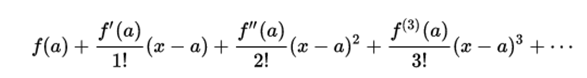
which can be written in a more compact way as the following sum:

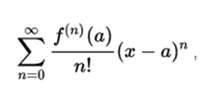
where:

• n! is the factorial of n
• f (n) (a) denotes the nth derivative of f for the value a of the variable with respect to which it is derived.
  The zero order derivative of f is defined as the proper f and both (x - a) 0 and 0i are both defined as 1 (0! = 1). If a = 0, as already mentioned, the series is also called McLaurin.

It should be noted that in a Taylor series of powers centered on the form 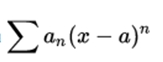you can always change the variable z = x-a (so that x = z + a in the original develop function) to express it as 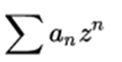centered on 0. Then you have to undo the change of variable. For example, if you want to develop the function 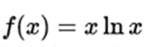around a = 1 you can take z = x-1, so it would develop 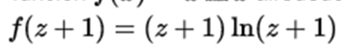centered on 0.

History

The elea philosopher Zeno of Elea considered the problem of adding an infinite series to achieve a finite result, but dismissed it as impossible: the result was Zeno's paradoxes. Later, Aristotle proposed a philosophical resolution to the paradox, but the mathematical content of this was not resolved until Democritus and later Archimedes retook it. It was through Archimedes' exhaustive method that an infinite number of progressive geometric subdivisions could reach a finite trigonometric result. Regardless, Liu Hui used a similar method hundreds of years later.

In the fourteenth century, the first examples of the use of Taylor series and similar methods were given by Madhava de Sangamagrama, although today no record of his work has survived the years, writings of later Hindu mathematicians suggest that He found a number of special cases from the Taylor series, including those for the trigonometric functions of the sine, cosine, tangent, and arctangent.

In the seventeenth century, James Gregory also worked in this area and published several series of Maclaurin. But in 1715 a general form was presented to build these series for all the functions for which it exists and was presented by Brook Taylor, from whom he gets his name.

The Maclaurin series were named after Colin Maclaurin, a professor from Edinburgh, who published the special case of the Taylor series in the 18th century.

Analytical function

If a Taylor series converges for all x belonging to the interval (a-r, a + r) and the sum equals f (x), then the function f (x) is called analytic. To check if the series converges to f (x), we usually use an estimate of the rest of Taylor's theorem.

A function is analytic if and only if it can be represented with a series of powers; the coefficients of that series are necessarily those determined in the formula of the Taylor series.

A function is usually approximated by a finite number of terms in its Taylor series. The Taylor Theorem facilitates the quantitative estimation of the error of said approximation. The Taylor polynomial is called the finite number of the initial terms of the Taylor series of a function. The Taylor series of a function is, if it exists, the limit of the Taylor polynomial of that function. A function may not be equal to the Taylor series or even converging such a series for each point. A function equal to its Taylor series in an open interval (or a disk in the complex plane) is called an analytic function.

Notable MacLaurin series

Below are some Taylor series of basic functions. All developments are also valid for complex values of x.

Exponential function and natural logarithm

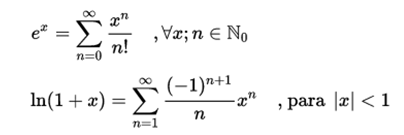
Geometric series

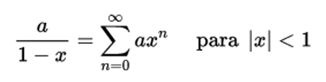
Trigonometric functions

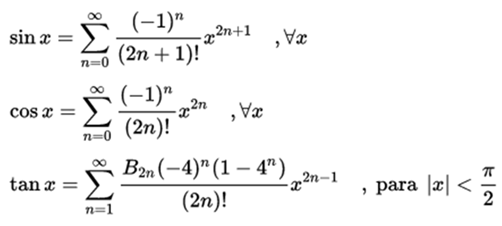
The cosine function

Where Bs are the Bernoulli Numbers.

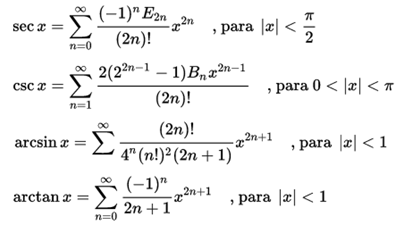
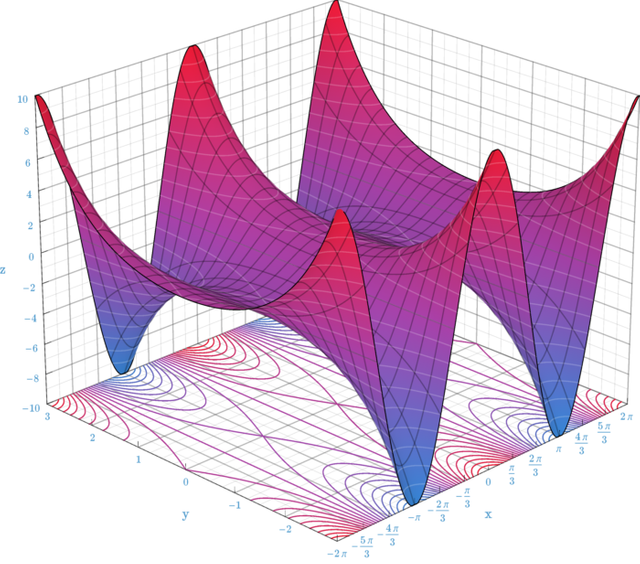
An eighth order approximation of the cosine function in the plane of the complexes.

Hyperbolic functions

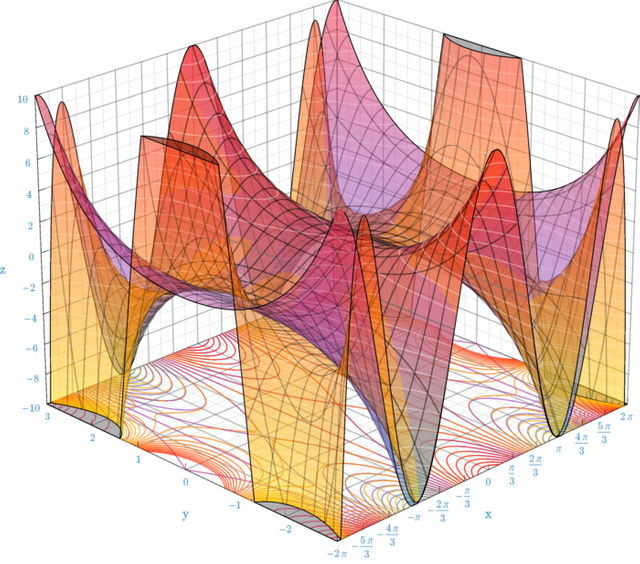
The two upper images together.

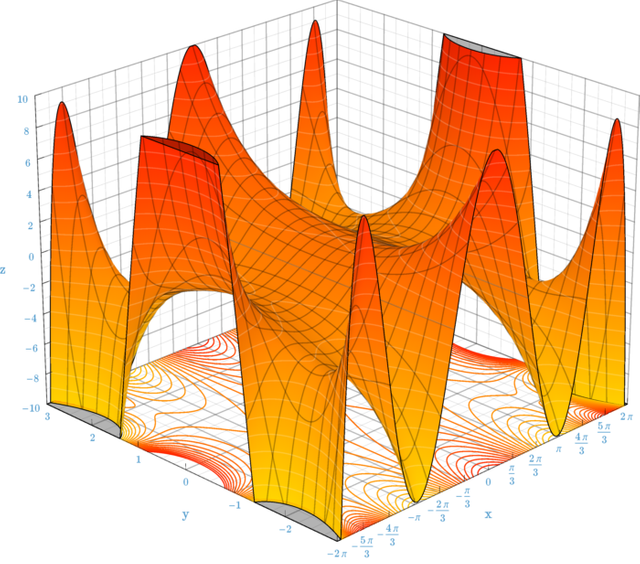
Lambert function W

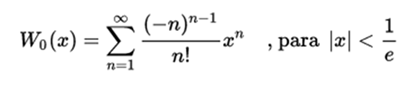
The numbers Bk that appear in the developments of tan (x) and tanh (x) are Bernoulli Numbers. The C (α, n) values of the binomial development are the binomial coefficients. The Ek of the development of sec (x) are Euler Numbers.

Several variables

The Taylor series can be generalized to functions of d variables:

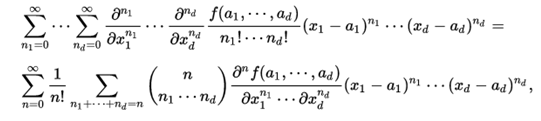
where 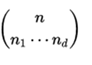is a multinomial coefficient. As an example, for a function of 2 variables, x and y, the Taylor series of second order in an environment of point (a, b) is:

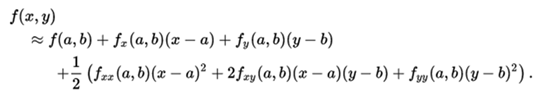
A second-degree Taylor polynomial can be written compactly like this:

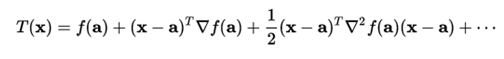
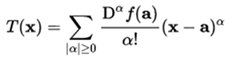
Applications

In addition to the obvious application of using polynomial functions instead of more complex functions to analyze the local behavior of a function, the Taylor series has many other applications.

Some of them are: analysis of limits and parametric studies of them, estimation of irrational numbers limiting their error, L'Hopital's theorem for the resolution of indeterminate limits, study of stationary points in functions (relative maximums or minimums or points chairs of strictly increasing or decreasing trend), estimation of integrals, determination of convergence and sum of some important series, study of order and main parameter of infinitesimuses, etc.

References

• Kline, M. (1990) Mathematical Thought from Ancient to Modern Times. Oxford University Press. pp. 35-37.
• Boyer, C. and Merzbach, U. (1991) A History of Mathematics. John Wiley and Sons. pp. 202-203.
• «Neither Newton nor Leibniz - The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala». MAT 314. Canisius College. Archived from the original on August 6, 2006. Retrieved on July 9, 2006.

Source :

https://es.wikipedia.org/wiki/Serie_de_Taylor