Interesting Airplane Riddle...
Interesting Airplane Riddle...
I saw this riddle in this book.
An airplane is going from New York to Los Angeles and back again.
There's 0 mph wind (no wind at all).
The distance is approximately 2,800 miles and typical cruising airspeed is around 550mph.
This means that the round trip (assuming no landing time and whatnot) would take
2*(2800/550) = 10.18 hours.
Now the question is...would the round trip time be greater, less, or equal with an easterly wind.
It's not too easy to see, because in one direction it will make your trip shorter and in the other direction it will make your trip longer...

Let s be the speed of the wind.
Then our effective speed from New York to LA is (550 - s) and our effective speed from LA to New York is (550 + s).
This might make you think that these cancel out and that the total round-trip time is unaffected, however consider what would happen if s = 550. Then it would take infinite time to get from New York to LA so clearly the wind speed does effect round trip time...
But how...
Time = Distance/Rate.
This means that our round trip time with wind can be written as follows:
Time = 2800/(550 - s) + 2800/(550 + s)
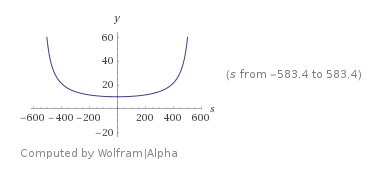
So from the graph above you can see that the round trip time is minimized when wind speed equals 0 mph...However if the speed of the wind gets faster than the speed of the airplane...then it can become a different story...and the original airplane speed becomes negligible as the wind throws around the airplane...
This was interesting. I definitely fell into the trap of thinking that the wind speed would cancel itself out. Playing with the numbers a little bit shows us that this isn't the case. It reminds me of my first calculus course in high school, in which I learned not to trust my first instinct when a problem can be worked out with some hypotheticals and a little bit of math.
And now a question for any experts that might see this: Could wind speeds realistically get that fast in an area so widespread that a plane could not avoid it? If not, the flight won't be impossible, we would just have to do more math to figure out how long it takes to detour around the windy area when it's not in your favor. This is a bit out of scope, being the difference between real world problems and riddles, but I love how a riddle can start off simple yet provoke more in-depth thoughts.
Yeah...also I think winds vary largely based on elevation, so you could consider the cost in time for climbing to an elevation where the wind is less. Fun stuff! Glad you liked the post!
Oh, perhaps instead of flying around the wind, we could potentially save time by flying over or under it! Now we're thinking in 3-dimensional space!