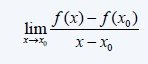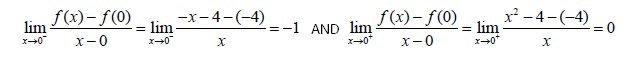Mathematics - Mathematical Analysis Derivatives
Hello its a me again! Today we will continue with Mathematical Analysis getting into Derivatives, differentiation rules and common derivatives. I leave out theorems and more in-depth examples for the next post! To understand better I suggest you to check out the Limits and Continuity post first. So, without further do let's get started!
Derivatives:
Using the Limits and Continuity that we already talked about we can now get into the concept of derivatives. Derivatives are part of the differential calculus and are a fundamental part of mathematical analysis in general.
Introduction:
So, why are they useful? The answer is simple, suppose you want to calculate the velocity of an object knowing the path/function that this object follows. The differentiation of his position with time will measure quick (amount of change) the position changes by time. The value of the derivative at some point actually tells us the slope of the tangent line at that point.
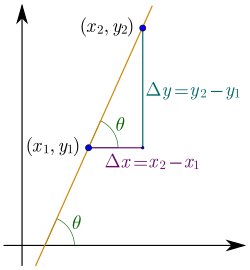
We actually already know the derivative of any point that is a part of a linear function by using the tangent of the angle ω between the line ε the linear function "draws" and the axis xx'.
So, the derivative is a = tan(ω) = y2 - y1 / x2 - x1.
This makes us think about the derivative as the quotient of the change of y (Δy) and x (Δx).
Definition:
Well, does this mean that we can also apply the same for any function by saying:
Derivative at (x0, f(x0)) = f(x) - f(x0) / x - x0 (where (x, f(x)) is some point "near" x0) ??
No, it doesn't! Think about cases where we have a indeterminate form like 0/0 or ∞/∞.
So, tell me how did we solve indeterminate forms? Limits, you're right and this changes the definition having the quotient inside of a limit where x goes to x0.
Finally, we ended up with how we define a derivative.
The definition looks like this:
f'(x0) = dy/dx = lim x->x0 [f(x) - f(x0) / x - x0]
where f'(x0) is Lagrange's notation and dy/dx Leibniz's notation.
I prefer using Lagrange's in most cases!
Differentiability at point:
Suppose a function f that is defined in the range (a, b) and a point x0 in that range.
This function is differentiable at x0 only when the following limit exists and has a real value:
The limit value is called the derivative of f at the point x0 and is noted as f'(x0).
Tangent at point:
Suppose a function f, the point A(x0, f(x0)) and that the derivative f'(x0) exists.
The tangent of f at the point A is a line that contains A and has a slope f'(x0).
This means that the tangent line equation looks like this:
y - f(x0) = f'(x0)*(x - x0)
Example:
Suppose the function f(x) = -x - 4, when x<0
= x^2 - 4, when x>=0
- Is the function differentiable at the point x = 0?
- Can we define a tangent for the point A(2, f(2))?
We have that f(0) = 0^2 - 4 = -4.
The one-sided limits at x0 = 0 look like this:
These two limits are different and so the limit is non-existent and thus we have that the function f is non-differentiable at the point x = 0.
Attention! Don't confuse these limits with the continuity limits. We don't have to get a value equal to f(x0), but the two one-sided limits need to have the same value! (We will later on see that a function that is differentiable is also continuous at that point, but not all continuous functions are differentiable)
For the tangent line we simply have to calculate the derivative at point A and fill in the equation we talked about previous. So, f'(2) = 4 (we will talk about rules in a sec) and that way we have:
y - f(2) = 4(x - 2) => y - 0 = 4*x - 8 => y = 4*x - 8.
Differentiation Rules:
- Multiplication with constant c -> [cf(x)]' = cf'(x)
- Sum/Difference of functions f, g -> [af(x) +- bg(x)]' = af'(x) +- bg'(x)
- Product of f, g -> [f(x)*g(x)]' = f'(x)g(x) + f(x)g'(x) (can be generalized to more, by having one of the functions in the product be "differentiated" at the time, followin the pattern)
- Quotient of f, g -> [f(x)/g(x)]' = (f'(x)g(x) − g'(x)f(x) ) / g(x)^2 (looks similar to the product one, but we this time have a minus and also divide with the denominator squared)
- A special case of the previous one is the so called Reciprocal -> [1/f(x)]' = −f'(x)/ f(x)^2
- Composition of f and g (chain rule) -> (fog(x))' = f'(g(x))*g'(x) that can also be written with Leibniz notation as dy/dx = (dy/du)*(du/dx), with y = f(u) and u = g(x), that makes us understand it better!
Common Function Derivatives:
- Constant -> (c)' = 0
- Line -> (x)' = 1 or (ax)' = a
- Power -> (x^n)' = x^n*(x^n-1), so the square (x^2)' = 2x
- Square root -> [root(x)]' = [x^1/2]' = (1/2) * x^(-1/2) from the power rule
- Exponential -> (a^x)' = a^x * lna and so (e^x)' = e^x, cause lne = 1
- Logarithms -> [loga(x)]' = 1/(x*lna) and so lnx = 1/x, cause lne = 1
- Trigonometric and inverse functions that you can check out here
- Hyperbolic and inverse functions that you can check out here
Examples:
We will calculate the derivative of the following functions:
1. f(x) = x*e^x
We use the product rule and this gives us:
f'(x) = [x*e^x]' = x'e^x + x*(e^x)'.
The derivative of e^x is equal to itself and x' equals 1 and so we end up with:
f'(x) = e^x + x*e^x = e^x*(1 + x)
2. g(x) = x^2 / lnx
We use the quotinet rule and this gives us:
g'(x) = [x^2 / lnx]' = [(x^2)'*lnx - x^2*(lnx)'] / (lnx)^2
We know that the square derivative is equal to 2x and that lnx = 1/x and so:
g'(x) = [2x*lnx - x^2*(1/x)] / (lnx)^2
Simplify a little more and we get the final result:
g'(x) = (2x*lnx - x) / (lnx)^2
3. h(x) = arctan(5x^2) , where arctan is the inverse function of tan
We have a composition and so we will differentiate each part separately:
[arctan(5x^2)]'y = dy/du = 1/(1+y^2) = 1/(1+(5x^2)^2) = 1/(1+25x^4).
(5x^2)'x = du/dx = 2*5x = 10x.
So, our final result is:
[arctan(5x^2)]' = [1/(1+25x^4)] * 10x = 10x / (1+25x^4)
And this is actually it for today and I hope you enjoyed it!
Next time we will get into Differentiation Theorems and Examples as I already told you in the beginning of this post.
Until next time...Bye!