A Neat And Easy Way Of Multiplying Two Numbers Together
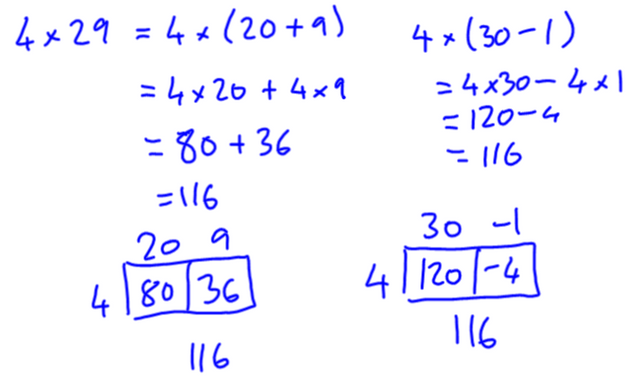
Hi there. This post is about a neat way to multiply two numbers together. It involves the concept of the distributive law from (high-school) mathematics and algebra.
The distributive law in (high-school) mathematics is a neat law where one term is multiplied with a sum of two or more terms. Some examples of this scenario include:
5(x + 7), 7(x + y + z), x(3x + 5y - 2z)
How The Distributive Law Works
In regular multiplication, 5 multiplied by 7 would simply be 5 x 7 = 35. If we have something like 3(x + 2), this would be 3(x + 2) = 3x + 6. The three on the left side multiplies with the x for the first term and the same three multiplies with the 2 to create the second term of 6.
Here is another example. The expression 8(x + 2y - 3z) can be expanded by the distributive law into:
8(x + 2y - 3z) = 8x + 8(2y) + 8(-3z) = 8x + 16y - 24z
The 8 from the left multiplies with every single term in the bracket. Be careful of negative signs!
An Alternate Way Of Using The Distributive Law
This alternate way of the distributive law helps with mental math and multiplication. After learning this, you may reduce the need for a calculator when it comes to multiplying higher numbers.
Example One
Multiplying 13 and 7 together can be hard on the brain. However, if you decompose the 13 into something like 10 and 3, you would have:
13 x 7 = (10 + 3) x 7 = 10 x 7 + 3 x 7 = 70 + 21 = 91
Note that the distributive law is applied from the right instead of from the left.
Example Two
What is 8 x 37?
With the distributive law in mind, we have:
8 x 37 = 8 x (30 + 7) = 8 x 30 + 8 x 7 = 8 x 3 x 10 + 56 = 240 + 56 = 296
You could skip the one step if you know that 8 x 30 = 240 right away.
Example Three
Here is one more example. What is 16 x 8?
One way of doing this is:
16(8) = (10 + 6) x 8 = 10 x 8 + 6 x 8 = 80 + 48 = 128
Note
You do have a choice in decomposing the numbers. In example one, I split the 13 into 10 + 3. You could split the 13 into 6 + 7 instead.
This post does not add up. LOL Just kidding. Nice post. Love logic!
Thanks. This seems to be the preferred way in primary schools.
You may like to do a follow-up when both numbers have 2 digits.
!-=o0o=-!
To follow curated math content follow @math-trail.
If you wish @math-trail to follow you then read this article.
I do plan on having a follow-up to this. It would be based on multiplying binomials and the FOIL method.
I've actually never seen this in my young learning in primary school. It depends on the teacher/school, I suppose.