An Introduction to Mathematical Proofs, Part 2: Conditionals, Deduction, Biconditionals, Proofs of Equivalence

This is part 2 of a multi-part series aimed at increasing mathematical literacy and logical thinking by teaching the background for and then the process of proving mathematics theorems. But this is important for more than just mathematicians: the ability to think logically is the backbone of making strong arguments and is vital for every aspect of life.

If you missed part 1, read it here.

Summary of what was covered in part 1:

-Propositions are sentences that are either true or false.
-Compound propositions are finitely many propositions connected by logical symbols
-Propositional forms are expressions involving finitely many logical connectors and letters.
-a paradox is a sentence that leads to a self-contradictory conclusion.
-Use letters such as P, Q, R, S to shorthand propositions
-"P and Q" = P^Q, referred to as conjunction
-"P or Q" = P v Q, referred to as disjunction
-"not P" = ~P, referred to as negation
-truth tables with N propositions have 2^N lines
-When two compound propositional forms have identical truth tables they are equivalent
-Tautologies are always true regardless of truth assignments to individual propositions, i.e. P v ~P
-Contradictions are the negation of tautologies. i.e. ~(P v ~P)

Conditionals

The most important kind of proposition in mathematics is a sentence of the form “If P, then Q”. This can be thought of as “P implies Q” or “if P is true then Q is necessarily true”. For example, “if X = 6, then 5 * X = 30” is a true sentence of this form because when X is 6, 5X is 30. But “if X = 6, then 5 * X = 20” is a false sentence of this form, because when X is 6, 5X is not 20.

Basically, a statement of the form “if P then Q” is true when the truth of P forces the truth of Q.

Definitions:

conditional sentence: Given propositions P and Q, "P => Q" is the proposition “if P then Q”. We use the “=>” symbol to denote “implies”.
antecedent: in the above example, the proposition P, or what is assumed.
consequent: in the above example, the proposition Q, or what is deduced.

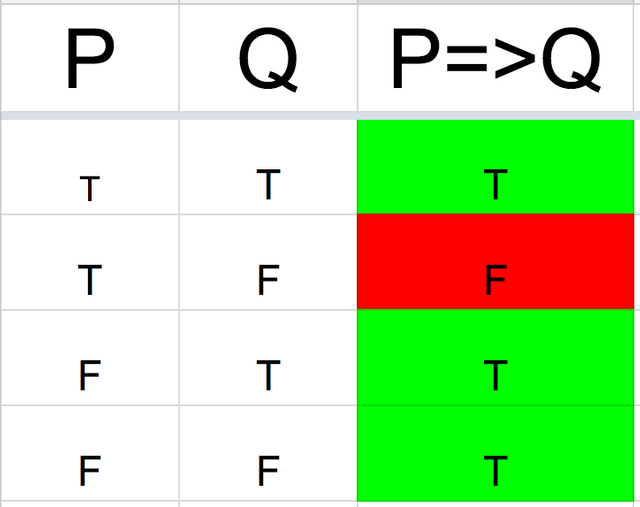
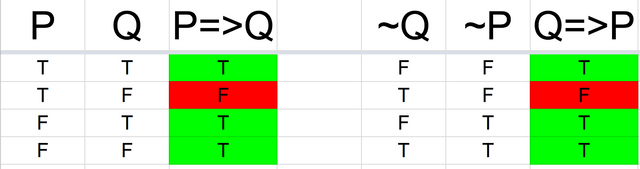
Think of the conditional sentence in the logical form “if P is true then Q is necessarily true”. P => Q is true whenever P (the antecedent) is false or Q (the consequent) is true. If P is false then the value of Q can be anything since our assumption is not met, but if P is true then Q must be true for P=>Q to be true.

Truth Table for P => Q:

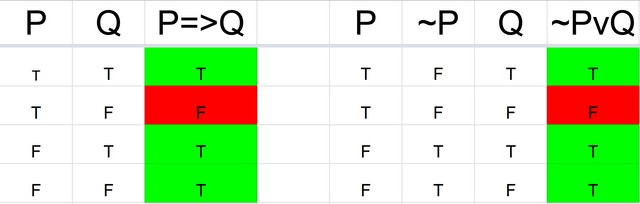
The truth table for P => Q is only false when P is true and Q is false. In every other case the “if P is true then Q is necessarily true” requirement is met. So logically, the conditional is equivalent to “not P or Q”: either P is false or Q is true”.

A check on the truth table of ~P v Q shows it is exactly equal to P => Q:

Modus Ponens Deduction

If we assume that both P and P => Q are true, then we can deduce Q is true:

This is essentially a larger conditional in the form [P ^ (P => Q)] => Q, with [P ^ (P => Q)] as the antecedent, and Q as the consequent. Just as before, to verify this conditional is true, we only need to check that when the antecedent is true, the consequent is necessarily true. We ignore the 3 cases where the antecedent is false, and in the one case when it is true, Q was true as well. Thus, we have deduced that when P and P=>Q are both true that Q is true too.

This is our first rule of deduction and is referred to as modus ponens: this is latin for “the way that affirms by affirming”. It is incredibly obvious: we say “if P is true then Q is true”, and then we assume P is true, we know that Q is true. It’s the simplest deduction we can make, but is incredibly important for building up to more complex rules and deductive logic.

This will be the basis for our first proof technique later on: the direct proof.

Converse and Contrapositive

For propositions P and Q, the converse of “P => Q” is “Q => P” and the contrapositive of “P => Q” is “~Q => ~P”.

Example:
Let P = “X = 6”
Let Q = “X^2 = 36”
The conditional, or P => Q is “if X is 6 then X squared is 36”.
The converse, or Q => P is “X squared is 36 implies that X is 6”.
The contrapositive, or ~Q => ~P is “If X squared is not 36, then X is not 6.

Note that in this case the converse is false: if X^2 is 36, then X could be either positive or negative 6 since (-6)^2 = 36 as well as (6)^2=36. Thus, the converse is false, and it is not necessarily true if the conditional is true.

But the contrapositive remains true: if X squared isn’t 36 then X cannot be 6.

Let’s prove these two theorems using proof tables:
The propositional form P => Q is not equivalent to its converse, Q => P.
The propositional form P => Q is equivalent to its contrapositive, ~Q => ~P.

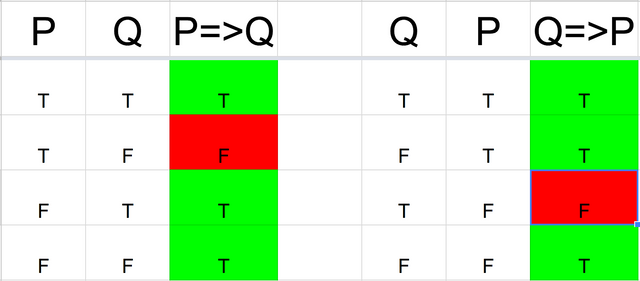
Truth Table For Converse:

The truth tables for P=>Q and Q=>P are different in two spots, so they are not equivalent.

Truth Table For Contrapositive:

The truth tables for P=>Q and ~Q=> ~P are the same on every line, so they are equivalent.

The equivalence of a conditional sentence and its contrapositive will be the basis for another one of the proof techniques we use a few lessons down the road, called Proof by Contraposition. Essentially, we can prove a statement of the form P=>Q if we prove that not Q implies not P since they are equivalent.

Biconditional Sentences

A biconditional sentence P <=> Q is the combination of both P=>Q and Q=>P. The double arrow <=> is a shorter way of saying (P=>Q)^(Q=>P). In english, P <=> is the proposition ”P if and only if Q”. The sentence is true exactly when P and Q have the same truth values.

Truth Table for “if and only if”:

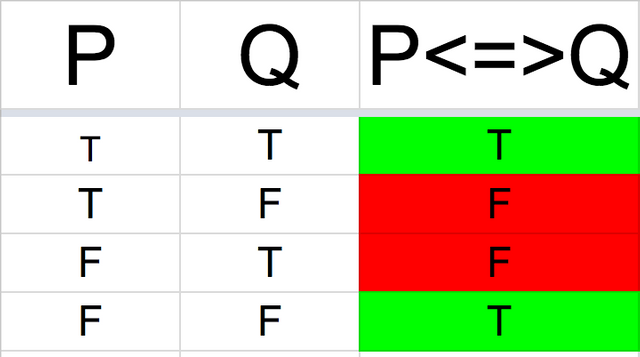
Mathematicians abbreviate “if and only if” as “iff” for shorthand purposes

Example:
“A rectangle is a square iff all four sides of the rectangle have equal length.”
A rectangle being a square implies that all four sides have equal length. But all four sides of a rectangle having equal length implies that the rectangle is a square. Thus P=>Q and Q=>P so P<=>Q, or P iff Q.

Equivalences

For propositions P, Q, and R, the following are equivalent:

1. P => Q is equivalent to (~P) v Q
2. P <=> Q is equivalent to (P=>Q) ^ (Q=>P)
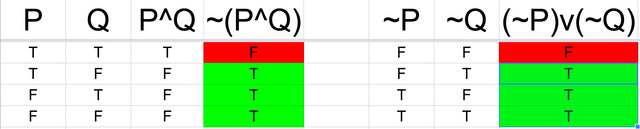
3. ~(P^Q) is equivalent to (~P) v (~Q)
4. ~(PvQ) is equivalent to (~P) ^ (~Q)
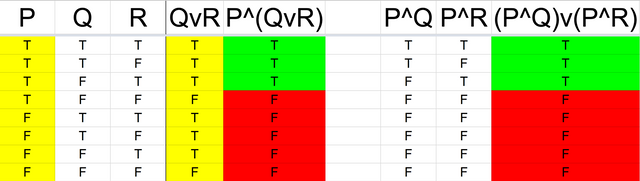
5. P^(QvR) is equivalent to (P^Q) v (P^R)
6. Pv(Q^R) is equivalent to (PvQ) ^ (PvR)

We already proved #1 and #2 using truth tables before.

#3 and #4 are De Morgan’s Laws. Let’s prove #3 using a truth table (#4 will have a similar proof):

De Morgan’s Laws distribute negation over conjunction in #3 and disjunction in #4.

#5 and #6 are Distributive Laws. Let’s prove #5 using a truth table (#6 will have a similar proof):

Armed with these equivalences, we can now prove other equivalences without the use of truth tables. For instance, suppose we want take a look at ~(P=>Q) and want to find out what it is equivalent to:
~(P => Q) is equivalent to ~(~P v Q) via #1.
~(~P v Q) is equivalent to P^~Q via #4.
Thus by the transitive property, ~(P => Q) is equivalent to P ^ (~Q).

The equivalences you can prove will grow steadily more complex, but using a set of basic rules we can now perform proofs without truth tables.

Translating English Phrases Using Logical Symbols

Shown below are phrases in English that are usually translated using connectives => and <=>, with examples to help make sense of them.

Use P=>Q to translate:

"if P, then Q”
Example: if x>10 then x>7.

"P implies Q”
Example: x>10 implies x>7.

"P is sufficient for Q”
Example: x>10 is sufficent for x>7

"P only if Q”
Example: x>10 only if x>7

"Q, if P”
Example: x>7 if x>10

"Q whenever P”
Example: x>7 whenever x>10

”Q is necessary for P”
Example: x>7 is necessary for x>10

Use P <=> Q to translate:

"P if and only if Q”
Example: |x|=3 if and only if x^2=9

”P is equivalent to Q”
Example: |x|=3 is equivalent to x^2=9

Summary:

-conditionals have the form “if P then Q”
-antecedent refers to the proposition P, or what is assumed.
-consequent refers to the proposition Q, or what is deduced.
-Modus Ponens is the first deductive logic rule, which states that if we know P and P=>Q then we can deduce Q. This sets up our first future proof technique, The Direct Proof.
-the converse of P=>Q is Q=>P, and it is not equivalent to the conditional.
-the contrapositive of P=>Q is ~Q => ~P, and it is equivalent to the conditional P=>Q. This sets up our second future proof technique, The Proof by Contraposition.
-biconditional sentences have the form “P if and only if Q”
-De Morgan’s Laws are two famous equivalences:
~(P^Q) is equivalent to (~P) v (~Q)
~(PvQ) is equivalent to (~P) ^ (~Q)
-**The distributive Laws are two famous equivalences:
P^(QvR) is equivalent to (P^Q) v (P^R)
Pv(Q^R) is equivalent to (PvQ) ^ (PvR)

Other great Mathematics Articles I’ve read:

An introduction to group theory by @complexring
Part 2 of introduction to group theory by @complexring
Pascal’s Triangle - The “Swiss Army Knife” of Mathematical Tools by @team-leibniz
L’Hopital’s Rule - A 17th Century Story of Paying for Content Curation by @team-leibniz

I welcome any other math threads or people I should follow in the comment section.

---

My name is Ryan Daut and I would love to have you as a follower. Click here to go to my profile page, then click Follow in the upper right corner if you would like to see my blogs and articles regularly. My interests include poker, fantasy sports, puppies, health and fitness, mathematics, astrophysics, cryptocurrency, and computer gaming.

You can also follow me on twitter.