The Chain Rule

---

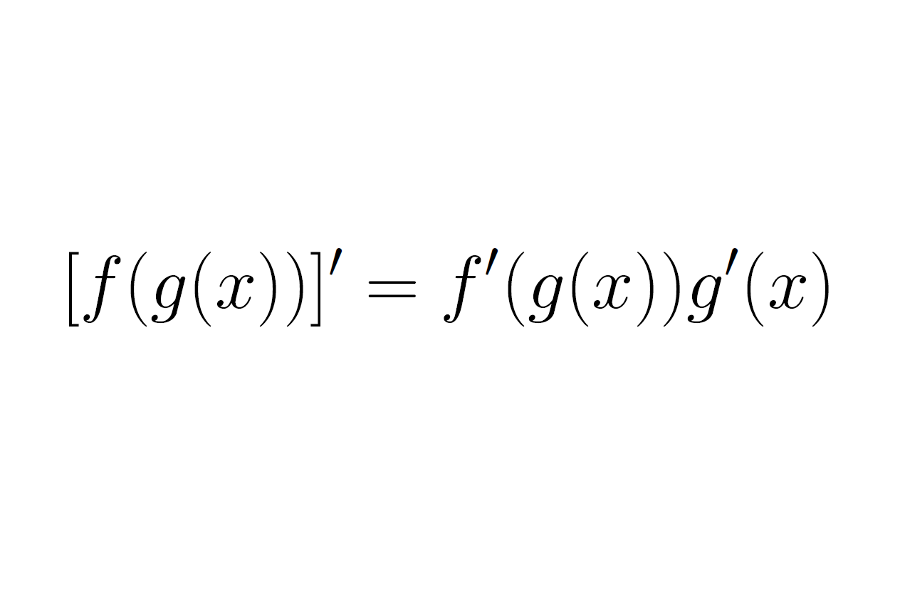
In calculus there are several different rules for taking the derivative of certain types of functions. For example, we have the power rule, the product rule and the quotient rule. In this post I will discuss the most powerful rule of them all which is called the chain rule and I will give a couple of examples of how this works.

The chain rule allows us to take the derivative of the composition of two differentiable functions. The chain rule is the following:

---

Chain Rule:

Suppose that f and g are differentiable functions then [f(g(x))]' = f'(g(x))g'(x)

---

Thus the chain rule tells us that the derivate of the composition of f(x) and g(x) is equal to the derivative of f(x) evaluated at g(x) times the derivative of g(x). I will now go over several examples of how to use the chain rule.

For the first example suppose that we want to find the derivative of h(x) = sin(2x). Then we can see that h is the composition of the two functions f(x) = sin(x) and g(x) = 2x. According to the chain rule we first find f'(x) = cos(x) and evaluate this derivative at g(x) to get f'(g(x)) = cos(2x). Next we find g'(x) = 2. According to the chain rule we have h'(x) = cos(2x)2.

For our second example we will find the derivative of h(x) = e^x2. Here we have f(x) = e^x and g(x) = x². We first calculate f'(x) = e^x and evaluate this derivative at g(x) to get f'(g(x)) = e^x2 and then multiply by g'(x) = 2x to get h'(x) = e^x22x.

Once we become more familiar with the chain rule we will begin to do it without writing out all of the steps as in the previous two examples. There is a saying used which helps us to remember the main idea of the chain rule. We can calculate the derivative of the composition of two functions by taking the derivative of the outside function f times the derivative of the inside function g. Although it is not mentioned in this phrase, technically we want the derivative of f evaluated at g.

Using this idea let us find the derivative of the function h(x) = (2x + 3)³. In this case the outside function is x³ and the inside function is 2x + 3. So according to the chain rule the derivative is h'(x) = (derivative of inside)(derivative of outside) = 3(2x + 3)²2 = 6(2x + 3)².

As the last example let us find the derivative of h(x) = cos(e^x + 1). The outside function is now cos(x) and the inside function is e^x + 1. According to the chain rule we have
h'(x) = -sin(e^x + 1)e^x

In this post we have introduced the chain rule and have given several examples of how to calculate the derivative of the composition of two differentiable functions. With the chain rule we are not limited to calculating the composition of only two functions. For example, if we wanted to find the derivative of the composition of three functions we would apply the chain rule twice to find the derivative. From this is should be clear that we can use the chain rule to find the derivative of compositions of any length and thus the chain rule provides a powerful tool for finding the derivative of complicated functions.

---

References:

https://en.wikipedia.org/wiki/Chain_rule
http://mathworld.wolfram.com/ChainRule.html

---

All the images in this post were created by myself using latex.