Mathematical Induction

---

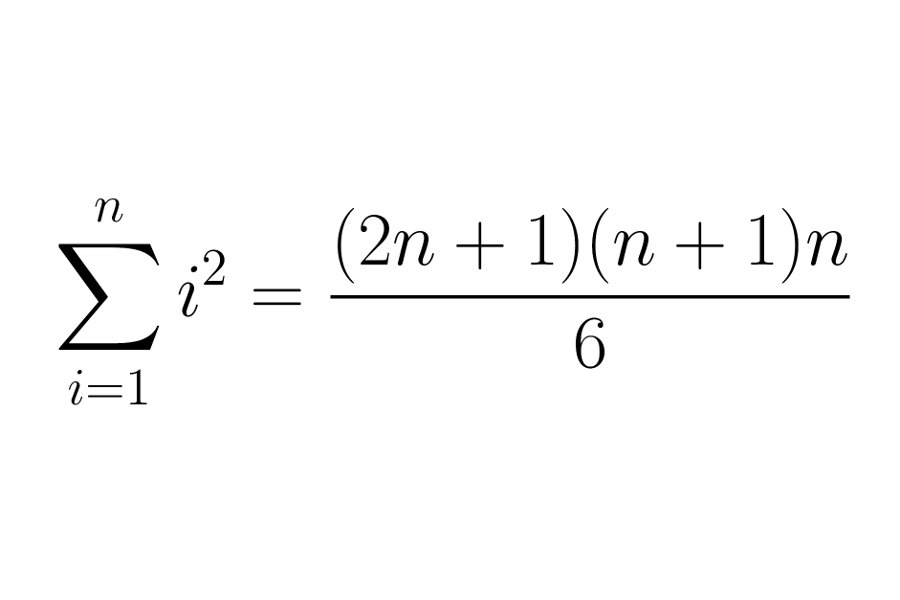
Mathematical induction is a basic technique used in mathematics to prove a statement holds for some set of numbers. Usually induction is applied to prove a statement that holds for the set of natural numbers and we will demonstrate some examples of how to do this in the current post.

The idea of induction is fairly simple and is one of the first tools that a mathematician will develop in their bag of mathematical techniques. We start with a given proposition which we will denote by P(n) where the n is meant to signify that our proposition is stated in terms of the natural number n. We would like to prove that the statement P(n) holds for every natural number. Since there are an infinite number of natural numbers we are technically proving an infinite number of propositions. However, induction allows us to do this easily in only a finite number of steps.

Mathematical induction proceeds as follows:

1. Prove that P(1) is true
2. Assume that P(n) is true for some n
3. Using that fact that P(n) is true prove that P(n+1) is also true

If we can establish the three steps listed above then by induction it follows that the statement P(n) holds for all the natural numbers n. Why does induction work? We know that P(1) is true due to step 1. From the fact that P(1) is true and that we have established steps 2 and 3 it follows also that P(2) is true. Since we know P(2) is true then using steps 2 and 3 again it follows that P(3) is true. With the same reasoning it should be clear that P(n) will hold for any n.

---

I will now give two examples of how to use mathematical induction involving sums of integers. For our first proposition we will take P(n) to be the following statement:

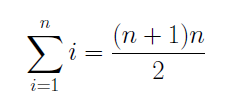
We will first show that P(1) is true. If we substitute n = 1 in to the statement we get the following:

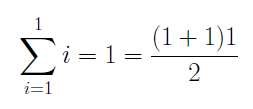
which shows that P(1) is true. We now assume that P(n) is true, that is the above statement holds for some n. Using the fact that P(n) is true we will prove P(n+1) is also true. We have

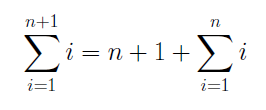
From step 2 we can replace the sum on the right side of the equality by

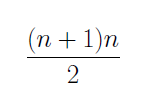
to get

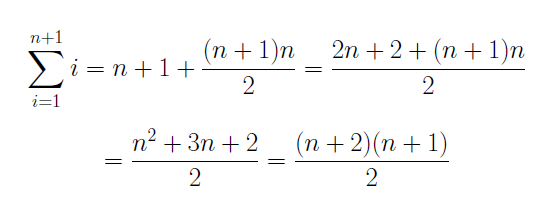
This last equality is just P(n+1) and so our proof is finished by mathematical induction.

---

For our second example we will prove the following proposition P(n):

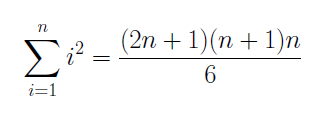
For P(1) the proof is a simple check as follows:

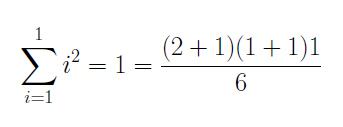
We now assume that P(n) is true for some n and prove that P(n+1) is true. We have

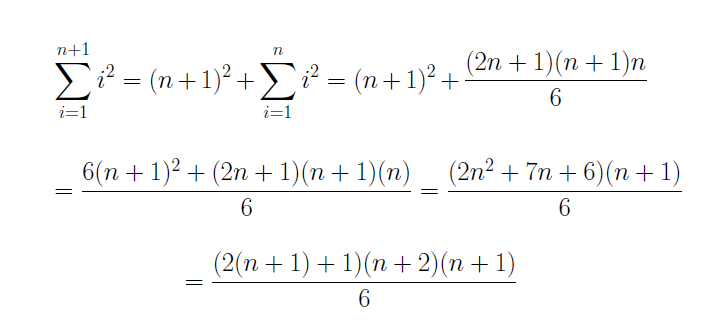
Thus it follows from induction that P(n) holds for all natural numbers.

---

For the above two examples we have used induction starting at the number n = 1. It is also common to use induction starting at n = 0 we just substitute P(0) instead of P(1) in to our first step of induction. Furthermore, induction can be started at any natural number we like just by changing the first step of the induction process.

---

References:

https://en.wikipedia.org/wiki/Mathematical_induction
https://en.wikipedia.org/wiki/Summation

---

All images in this post were created by myself using latex.