[Math Talk #4] Pigeonhole Principle and Applications [2]

mathsolver (53)in #math • 6 years ago (edited)

Pigeonhole Principle and Miscellaneous Applications (2)

[1]

Continuing our discussion of pigeonhole principle from Math Talk #3, I will post some miscellaneous applications of Pigeonhole principle.

1. Partitioning the subset of Natural numbers

1-1. Concerning the set $\left\{ 1, 2, ..., 2n \right\}$

Problem 1. - [2]
Given any $n+1$ integers among $\left\{ 1, 2, ..., 2n \right\}$ , show that two of them are relatively prime. Show that the result is false if we choose $n$ integers.

Solution 1.
Partition the set $\left\{ 1, 2, ..., 2n \right\}$ into $n$ subsets of the form

$\left\{ 1, 2 \right\}, \left\{ 3, 4 \right\}, ..., \left\{ 2n-1, 2n \right\}$

Then by Pigeonhole principle, choosing $n+1$ integers forces us to pick two (i.e. all ) elements in single partition. Since consecutive integers are relatively prime, there is at least one pair of integers which are relatively prime.

If the number reduces to $n$ , then clearly choosing $\left\{ 2, 4, 6, ..., 2n \right\}$ (the set of even numbers) will be the counterexample.

Problem 2. - [3]
Given any $n+1$ integers among $\left\{ 1, 2, ..., 2n \right\}$ , show that one of them is divisible by another. Show that the result is false if we choose $n$ integers.

Solution 2.
By prime factorizing theorem for positive integers, every positive integers can be expressed as

$k = 2^m \times \ell$

where $m \geq 0$ and $\ell$ is odd. First, make $n$ pigeonholes as follows.

$\left\{ 1 \right\}, \left\{ 3 \right\}, \left\{ 5 \right\}, ..., \left\{ 2n-3 \right\}, \left\{ 2n-1 \right\}$

In other words, every odd number less than $2n$ is partitioned into singleton sets. Now,

$k = 2^{m} \times \ell \leq 2n \implies \ell \leq 2n$

since $m \geq 0$ . Since there are $n$ distinct odd numbers, among $n+1$ numbers, there should exist two $k_1, k_2$ having same $\ell$ by pigeonhole principle. Then we can express as

$k_1 = 2^{m_1} \times \ell,\ k_2 = 2^{m_2} \times \ell \implies k_1 | k_2 \text{ or } k_2 | k_1$

depending on the magnitude of $m_1, m_2$ .

If the number reduces to $n$ , then clearly the set of all odd numbers $\left\{ 1, 3, 5,..., 2n-1 \right\}$ would be the counterexample.

Problem 3. - [4]
Let $a_1 < a_2 < ... < a_n$ and $b_1 > b_2 > ... > b_n$ where $a_1,...,a_n, b_1,...,b_n$ are all distinct elements in $\left\{ 1, 2, ..., 2n \right\}$ . Prove that

$\sum_{i=1}^{n} |a_i - b_i| = n^2$

Solution 3.
First, partition the whole set into two disjoint subsets

$\left\{ 1, 2, ..., n \right\}, \left\{ n+1, n+2, ..., 2n \right\}$

Now fix index $i$ , and consider $a_i, b_i$ . $a_1, a_2, ..., a_{i-1}, b_{i+1}, ..., b_n$ are all smaller than $\max(a_i, b_i)$ . So at least

$\max(a_i, b_i) > (i - 1) + (n - i) + 1 = n - 1 + 1 = n \implies \max(a_i, b_i) \geq n + 1$

So $\max(a_1, b_1), \max(a_2, b_2), ..., \max(a_n, b_n)$ are all elements of the latter set $\left\{ n+1, ..., 2n \right\}$ . Since

$\max(a_i, b_i) = \max(a_j, b_j) \implies i = j$

those $n$ elements of the form $\max(a_i, b_i)$ are all distinct, so that by Pigeonhole principle, they occupy exactly one element in $\left\{ n+1, ..., 2n \right\}$ .

Since $\min(a_i, b_i) < \max(a_i, b_i)$ and all $n$ elements of the form $\min(a_i, b_i)$ are distinct, by Pigeonhole principle, they occupy exactly one element in $\left\{ 1, 2, ..., n \right\}$ . So

$\begin{align*} \sum_{i=1}^{n} |a_i - b_i| &= \sum_{i=1}^{n} \left[ \max(a_i, b_i) - \min(a_i, b_i) \right] \\ &= \sum_{i=1}^{n} \max(a_i, b_i) - \sum_{i=1}^{n} \min(a_i, b_i) \\ &= (n+1 + n+2 + ... +2n) - (1+2+... n) \\ &= n^2 \end{align*}$

2. Erdös - Szerkes Theorem

The original theorem is as follows.

Theorem.
For given $r, s \in \mathbb{N}$ any sequence of distinct real numbers with length at least $(r-1)(s-1) + 1$ contains a monotonically increasing subsequence of length r or a monotonically decreasing subsequence of length s.

Proof. - [5]
First denote $(r-1)(s-1) + 1$ as $n_1, n_2, ..., n_{(r-1)(s-1)+1}$ . Also for each $n_i$ , we assign a pair $(a_i, b_i)$ such that

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n_i \mapsto (a_i, b_i)\\ a_i:= \text{length of longest monotonically increasing subsequence ending in }n_i\\ b_i:= \text{length of longest monotonically decreasing subsequence ending in }n_i$

Now we seek some properties of this pair. Since all numbers are distinct,

$i < j\ \land n_i \leq n_j \implies a_i < a_j$

as well as

$i < j\ \land n_i \geq n_j \implies b_i > b_j$

So, $(a_i, b_i) \neq (a_j, b_j)$ for any case.

If number of possible values of $a_i$ is less than $r$ and number of possible values of $b_i$ is less than $s$ , then in total, there will be at most $(r-1)(s-1)$ number of $(a_i, b_i)$ pairs. This contradicts to the fact that all pairs are distinct (which in total $(r-1)(s-1) + 1$ ), so by Pigeonhole principle, either

$a_i \geq r$

$b_i \geq s$

for some index $i$ .

2-1. Visualization of Theorem

Let's say we have $M=(r-1)(s-1) + 1$ distinct real numbers,

$n_1, n_2, ..., n_M$

Now in 2D $\mathbb{R}^2$ plane, math each number $n_i$ to the point $n_i \mapsto (i, n_i)$ . Then we can always find a polygonal path either

length $r-1$ and of positive slope. (Going upward right)
length $s-1$ and of negative slope. (Going downaward right)

Example

The case when $r = s = 5$ . Randomly generate $(r-1)(s-1) + 1 = 17$ points.
[6]

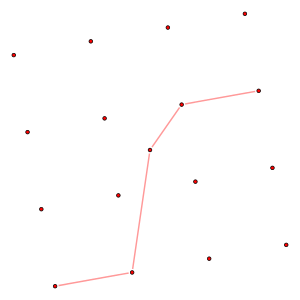
We can see that it consists of 5 $=r$ points, which is of positive slope polygon path.

3. Conclusion

Pigeonhole Principle can be a powerful tool in discrete mathematics and in any field concerning some counting.

4. Citations

[1] http://cpptruths.blogspot.com/2014/05/the-pigeonhole-principle-in-c.html (only image is used)

[2] http://web.archive.org/web/20120124185755/http://math.mit.edu/~rstan/a34/pigeon.pdf Problem 7

[3] http://web.archive.org/web/20120124185755/http://math.mit.edu/~rstan/a34/pigeon.pdf Problem 8

[4] http://web.archive.org/web/20120124185755/http://math.mit.edu/~rstan/a34/pigeon.pdf Problem 13

[5] Seidenberg, A. (1959), "A simple proof of a theorem of Erdős and Szekeres" (PDF), Journal of the London Mathematical Society, 34: 352, doi:10.1112/jlms/s1-34.3.352.

[6] https://en.wikipedia.org/wiki/Erd%C5%91s%E2%80%93Szekeres_theorem (only image is used)

**Solutions to the problems are made by myself. **

#mathematics #science #steemstem #mathsolver

6 years ago in #math by mathsolver (53)

$21.71

Sort:

Trending

[-]

alexs1320 (71) 6 years ago

Nice! Visualization of Theorem paragraph is just a beauty.

For non-math readers, relatively prime.

$0.06

1 vote

[-]

steemitboard (66) 6 years ago

Congratulations @mathsolver! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :

Award for the number of upvotes

_{Click on the badge to view your Board of Honor.}
_{If you no longer want to receive notifications, reply to this comment with the word STOP}

To support your work, I also upvoted your post!

You can upvote this notification to help all Steemit users. Learn why here!

$0.00

[-]

steemstem (73) 6 years ago

This post has been voted on by the steemstem curation team and voting trail.

There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!

$0.00

[-]

mathsolver (53) 6 years ago

Thanks a lot! I'll do my best to post quality materials in Steemit.

$0.00

[-]

alexdory (59) 6 years ago

Well done!
Don't forget to also engage with other authors as this is what builds the community. The best way to advertise your account in the beginning is to actually be a smart and considerate person.
Perhaps add a few words to the account description. That's your business card!
Thanks for joining us and I am here for help and for any question you have!
Nice country you have, I hope I will visit it soon, was in Thailand in December but I'd love to visit Korea or Japan soon.
Cheers!

$0.00

[-]

mathsolver (53) 6 years ago

Thanks a lot SteemSTem! I will add some descriptions on my account profile.

$0.00

STEEM 0.19

TRX 0.13

JST 0.030

BTC 62835.77

ETH 3392.04

USDT 1.00

SBD 2.50

[Math Talk #4] Pigeonhole Principle and Applications [2]

Pigeonhole Principle and Miscellaneous Applications (2)

1. Partitioning the subset of Natural numbers

1-1. Concerning the set

2. Erdös - Szerkes Theorem

2-1. Visualization of Theorem

Example

3. Conclusion

4. Citations

Coin Marketplace

1-1. Concerning the set $\left\{ 1, 2, ..., 2n \right\}$