[Math Talk #3] Pigeonhole Principle and its Usage

mathsolver (53)in #math • 6 years ago

Pigeonhole Principle in Mathematics

1. What is Pigeonhole Principle?

First, let's look at the following figure.

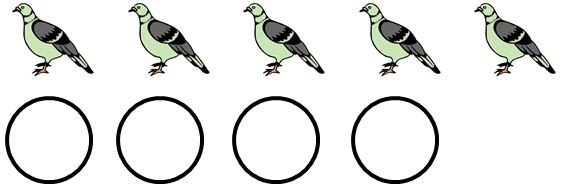
There are five pigeons, and four holes. Suppose we want to locate each pigeons into holes. Then since the number of holes is strictly less than the number of pigeons, there exist at least one hole which contains more than 1 (so, at least 2) pigeons. This is the basic concept of Pigeonhold principle. More formally, it can be stated as follows.

Pigeonhole Principle.

If $n$ items are put into $m$ containers, with $n>m$ then at least one container must contain at least $\lfloor n/m \rfloor +1$ items.

Well the proof is simple. By division algorithm of integers, $n = m \times \lfloor n/m \rfloor + r$ where $0 < r < m$ (it can not be zero, since $n>m$ ). So if all the containers contain at most $\lfloor n/m \rfloor$ items, then $m\lfloor n/m \rfloor \geq n \implies r \leq 0$ which is contradiction.

2. Its Usage?

Well you can think this is so trivial that no body will ever use it, but actually it is really useful as well as important principle in mathematics. Here are some examples.

2-1. Decimal Expansion of Rational Number

We already learned in Elementary school (well, at least without a proof) that every positive rational number is either terminating decimal or repeating decimal. This can be proved very easily by Pigeonhole Principle.

If the decimal terminates, it is not our interest; nothing more to prove.
Suppose the decimal does not terminate. We have to formulate our goal. Pick any positive rational number $r = q/p \in \mathbb{Q}^{>0}$ where $\gcd(p,q) = 1$ .

Since we assumed that decimal does not terminate, there exist a sequence $\left\{ a_n \right\}$ such that

$p/q = a_0 + \frac{a_1}{10} + \frac{a_2}{10^2} + ... = \sum_{n=0}^{\infty} \frac{a_n}{10^n}$

with the fact that $a_n \in \left\{ 0, 1, ..., 8, 9 \right\}$ .

Step 1. By division algorithm of integers, $p = q m_0 + r_0$ for some quotient $m_0$ and remainder $0 < r_0 < q$ . Then

$p/q = m_0 + r_0/q \implies a_0 = m_0$

Step 2. Now $r_0/q = \frac{a_1}{10} + \frac{a_2}{10^2} + ...$ . Again by division algorithm of integers, $10r_0 = q m_1 + r_1$ for some suitable quotient and remainder. Now

$\frac{10r_0}{q} = m_1 + \frac{r_1}{q} \implies a_1 = m_1$

Step 3. Inductively define the quotient and remainder by $10r_n = q m_{n+1} + r_{n+1}$ for $n=0,1,2,...$ . Then by pigeonhole principle, there should exist two indices $i, j$ such that $i <j$ and $r_i = r_j$ (because $0 < r < q$ ). After that point ( $j$ -th step), the division algorithm is just the repetition of what we did after the $i$ -th step.

Step 4. Let $j_0$ be the smallest index such that $r_{j_0} = r_i$ for some $i = 0, 1, 2, ..., j_0 - 1$ . $j_0$ surely exists by Well-Ordering Principle of natural numbers. Also pick the smallest index among such $i = 0, 1, 2, ..., j_0 - 1$ and denote it as $i_0$ . Then the final answer would be

$\frac{p}{q} = a_0.a_1a_2...a_{i_0 - 1}\overline{a_{i_0} a_{i+1}...a_{j_0}}$

Not only we've showed the desired result, but actually we've constructed the period with the help of Well Ordering Principle!

2-2. Dense subset of Real numbers

Pick any irrational number $\alpha \in \mathbb{R}$ . Then consider the set

$T = \left\{ \langle k\alpha \rangle: k \in \mathbb{Z}, \langle k \alpha \rangle = k\alpha - \lfloor k\alpha \rfloor \right\}$

which is the collection of all fractional part of integer multiple of $\alpha$ . Since it is the fractional part, $T \subset [0, 1]$ . Now the question is

Is $T$ dense in $[0, 1]$ ?

Well, it seems correct, because product between irrational number and integer is also irrational. Let's prove it using Pigeonhole principle.

First, let $\epsilon > 0$ be given. Pick any natural number $M \in \mathbb{N}$ such that $1/M < \epsilon$ . Then consider

$\langle \alpha \rangle,\ \langle 2\alpha \rangle,...,\ \langle M\alpha \rangle, \langle (M+1)\alpha \rangle$

If $\langle i\alpha \rangle = \langle j\alpha \rangle$ , then $(i-j)\alpha = \lfloor i\alpha \rfloor - \lfloor j \alpha \rfloor \in \mathbb{Z} \implies i = j$ , so it is clear that all $M+1$ elements are distinct. If we divide $[0,1]$ into $M$ equal intervals

$[0, 1/M],\ [1/M, 2/M],..., [1 - 1/M, 1]$

then by Pigeonhole Principle, any two distinct elements $\langle i\alpha \rangle, \langle j\alpha \rangle$ are in the same subinterval. Then it is clear that

$p + k/M <i\alpha < p + (k + 1)/M$
as well as
$q + k/M <j\alpha < q + (k + 1)/M$
for some integer $p,q, k$ . So,

$p-q - 1/M < (i-j)\alpha < p - q + 1/M$

This implies that $\langle (i - j) \alpha \rangle < 1/M < \epsilon$ , $0$ is a limit point of $T$ . Now we divide into cases.

If a point $p \in (0, 1]$ is in $(0, 1/M]$ , then we are done; because already we showed zero is a limit point of $T$ .
If a point is in some other interval of the form $\left( \frac{\ell}{M}, \frac{\ell + 1}{M} \right )$ , then take

$n = \sup \left\{ k \in \mathbb{N} : k\langle (i - j) \alpha \rangle < \ell/M \right\}$
. Since $\ell/M \leq (n + 1) \langle (i-j) \alpha \rangle < (\ell + 1)/M$ , we get the fact that such points are also limit points of $T$ .

So we've constructed a countable subset of $[0, 1]$ , which does not contain any rational numbers (except zero)!.

3. Conclusion

Well, the concept of pigeonhole principle is quite simple, but the usage is very broad and also deep. Combined with elementary analysis, we can deduce some useful facts about dense subset using pigeonhole principle!.

#mathematics #science #steemstem #mathsolver

6 years ago in #math by mathsolver (53)

$0.08

8 votes

STEEM 0.17

TRX 0.13

JST 0.027

BTC 58981.78

ETH 2669.36

USDT 1.00

SBD 2.44