[Math & Physics #11] Kepler's Law of Planetary Motion - Simple but Astonishing [Part 2]

mathsolver (53)in #math • 6 years ago

[1]

Kepler's Law of Planetary Motion - [Part 2]

Short but Astonishing

Continuing from the last talk (<Math & Physics #10>), in this post I will talk about Kepler's Second Law of Planetary motion - Equal Time Equal Area Law.

0. What is the second law of planetary motion?

It states that

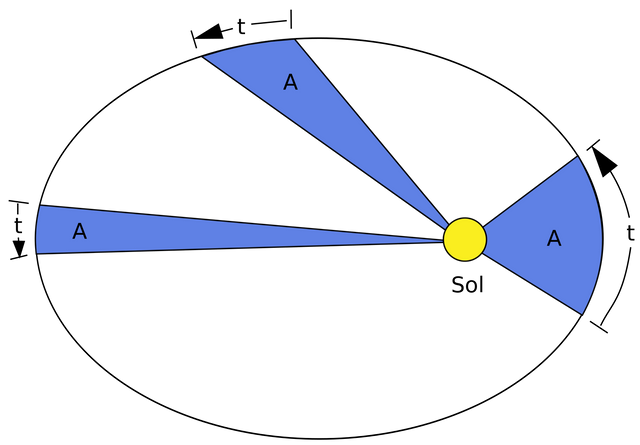
A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.

For example, look at the following figure.

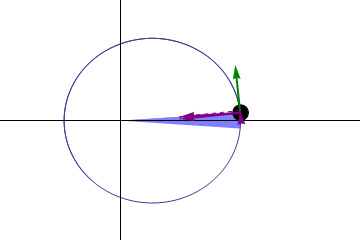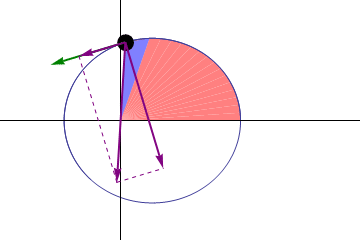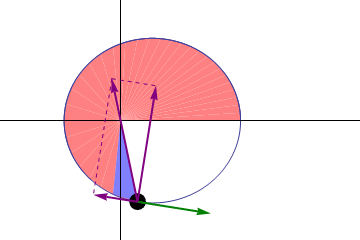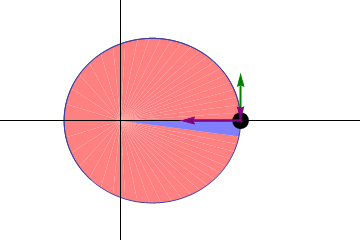
[2]

The planet is rotating around the sun (located at the origin) in elliptical orbit. To satisfy Kepler's second law, at the apoapsis (the point where the distance between the sun and the planet is maximum), the orbital velocity (green vector) should be minimized. On the contrary, at the periapsis (the point where the distance is minimum), the orbital velocity should be maximized. Note that each portion divided by white lines is equal.

1. History Behind the Second law

Johannes Kepler's second law of planetary motion first came out in 1609, in his paper <Astonomia Nova> [3] . At that time Kepler did not present his second law in its modern form. His law only applied to Mars. Kepler restated his second law in 1621, for any planet. In his paper <Epitome Astronomiae Copernicanae> [4], Kepler wrote

It has been said above that, if the orbit of the planet is divided into the smallest equal parts, the times of the planet in them increase in the ratio of the distances between them and the sun.) That is, a planet's speed along its orbit is inversely proportional to its distance from the Sun.

It is clear that Kepler was referring to what is now called angular velocity and the second law can be easily deduced from it.

2. The actual Verification

Honestly, the actual proof of Kepler's second law is extremely simple. Knowing little bit of vector calculus as well as Newtonian mechanics are enough. For proof I will use the following diagram.

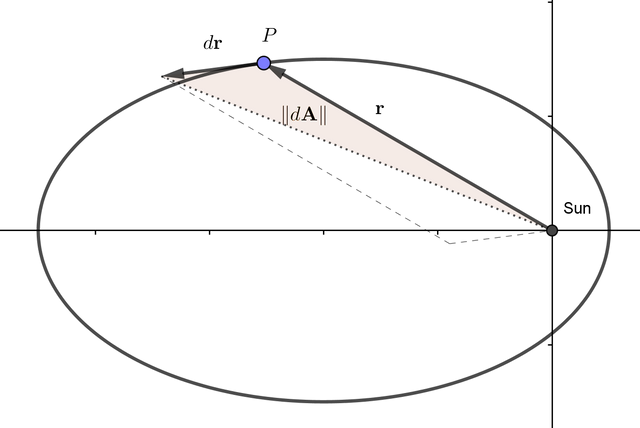
Define a vector from the sun to planet $P$ as $\mathbf{r}$ . In infinitesimal time $dt$ , the infinitesimal change of vector $\mathbf{r}$ is $d\mathbf{r}$ . Now, the infinitesimal area swept by the vector $\mathbf{r}$ during time $dt$ is equal to

$\lVert d\mathbf{A} \rVert = \frac{1}{2} \lVert \mathbf{r} \times d\mathbf{r} \lVert$

using cross product. (The magnitude of cross product is equal to area of parallelogram so we should take half of it). Now we will investigate the quantity

$d\mathbf{A} = \frac{1}{2} (\mathbf{r} \times d\mathbf{r} )$

The rate of sweeping out area due to movement is

$\begin{align*} \dot{\mathbf{A}} &= \frac{d\mathbf{A}}{dt} \\ &= \frac{1}{2} \left( \frac{d\mathbf{r}}{dt} \times d\mathbf{r} + \mathbf{r} \times \frac{d\mathbf{r}}{dt}\right)\ (\because d\mathbf{r} \times d\mathbf{r} = 0)\\ &= \frac{1}{2} \left( \mathbf{r} \times \dot{\mathbf{r}} \right ) \end{align*}$

Again differentiating both sides (respect to time) gives

$\begin{align*} \ddot{\mathbf{A}} &= \frac{d\dot{\mathbf{A}}}{dt} \\ &= \frac{1}{2} \left( \dot{\mathbf{r}} \times \dot{\mathbf{r}}+ \mathbf{r} \times \ddot{\mathbf{r}} \right)\\ &= \frac{1}{2} (\mathbf{r} \times \ddot{\mathbf{r}})\ (\because \dot{\mathbf{r}} \times \dot{\mathbf{r}} = 0) \end{align*}$

The vector $\ddot{\mathbf{r}}$ is nothing but the accerleration vector of $\mathbf{r}$ .

By Newton's second law of motion, the gravitational force $\mathbf{F}$ has same direction with the accerleration $\mathbf{r}$ . We all know that the gravitational force between two bodies has direction towards each other, so that

$\mathbf{r} \parallel \ddot{\mathbf{r}} \implies \mathbf{r} \times \ddot{\mathbf{r}} = 0$

We can therefore say that

$\ddot{\mathbf{A}} = 0 \implies \dot{\mathbf{A}} \equiv \mathbf{c}\ (\text{constant vector})$

Now

$\lVert d\mathbf{A} \rVert = \lVert \mathbf{c} dt \rVert = \lVert \mathbf{c}\rVert dt= cdt$

which means that the area swept by vector $\mathbf{r}$ is directly proportional to the time duration $dt$ . So if two intervals of time have equal length, then the area swept should also be equal, proving the Kepler's second law of planetary motion.

3. Velocity of the Planet

Remember the diagram we've seen in Section 0? The velocity of the planet changes at every point of the orbit. Especially, at apoapsis it's minimized, and at periapsis it's maximized. Take a loot at the following diagram.

Gravitation constant $G$ , the mass of sun $M$ and the mass of the planet $m$ .
Sun is located at the origin. (fixed)
A vector from sun to the planet $P$ is denoted by $\mathbf{r}$ , and the instantaneous velocity vector is denoted by $\mathbf{v}$ . In particular at apoapsis and periapsis, we use subscripts $a$ and $p$ .
The length of semi-major axis of the elliptical orbit is given by $a$ .

The Goal is to find the speed $v = \lVert \mathbf{v} \rVert$ , resepct to $r = \lVert \mathbf{r} \rVert$ .

Ingredients

Conservation of Mechanical Energy
By the conservation of mechanical energy, we get at any point on the orbit,

$\frac{1}{2}mv^2 - \frac{GmM}{r} \equiv E \text{ (constant)}$

Kepler's Second law of motion
From section 2, we obtained the fact $\dot{\mathbf{A}} = \frac{1}{2} (\mathbf{r} \times \dot{\mathbf{r}}) = \frac{1}{2} (\mathbf{r} \times \mathbf{v}) \equiv \text{constant}$ . Vector $\mathbf{r}$ and $\mathbf{v}$ are perpendicular to each other at two points (apoapsis & periapsis), so that

$\lVert \mathbf{r}_a \times \mathbf{v}_a \rVert = \lVert \mathbf{r}_p \times \mathbf{v}_p \rVert \implies r_av_a = r_pv_p$

Property of Ellipse

$r_a + r_p = 2a$

[5]
Now let's begin. Put $r_a, v_a$ and $r_p, v_p$ into energy equation.

$E = \frac{1}{2}m v_a^2 - \frac{GmM}{r_a} = \frac{1}{2}mv_p^2 - \frac{GmM}{r_p^2} \\ \implies \frac{v_a^2}{2} - \frac{v_b^2}{2} = \frac{GM}{r_a} - \frac{GM}{r_p}$

$v_p = \frac{r_a}{r_p} v_a$ via Kepler's law, so that

$\frac{1}{2} \left( 1 - \frac{r_a^2}{r_p^2} \right ) v_a^2 = GM \left( \frac{1}{r_a} - \frac{1}{r_p} \right ) \\\\\\ \iff \frac{1}{2} \left( \frac{r_p^2 - r_a^2}{r_p^2} \right ) v_a^2 = GM \left( \frac{r_p - r_a}{r_ar_p} \right )\\\\\\ \iff \frac{1}{2} \left( \frac{r_p + r_a}{ r_p^2} \right ) v_a^2 = \frac{GM}{r_ar_p}\ (\because r_p^2 - r_a^2 = (r_p + r_a)(r_p-r_a))\\\\\\ \iff av_a^2 = GM \frac{r_p}{r_a} = \frac{GM(2a - r_a)}{r_a}\ (\because r_a + r_p = 2a) \\\\\\ \iff \frac{1}{2}v_a^2 - \frac{GM}{r_a} = -\frac{GM}{2a}\ (\text{divide both sides by } 2a)$

So for any $r$ , we have

$E = \frac{1}{2}mv^2 - \frac{GmM}{r} = \frac{1}{2}mv_a^2 - \frac{GmM}{r_a} = - \frac{GmM}{2a}$

thus

$v = \sqrt{GM \left( \frac{2}{r} - \frac{1}{a} \right )}$

a simple result!

4. Analysis of the Results obtained in 2 & 3

Going back to verification steps in sections 2, you'll notice that the key concept we used to prove Kepler's Law was the fact that acceleration vector $\ddot{\mathbf{r}}$ is parallel to $\mathbf{r}$ . As long as the force between the planet and the sun is parallel to $\mathbf{r}$ , the proof is valid. Only the direction of the force matters, NOT the magnitude. So Kepler's second law not only applies to planets in gravitational field, but also to objects rotating around fixed body in any field satisfying

$\mathbf{F}(\mathbf{r}) \parallel \mathbf{r}$

;)

Suppose we want to launch a spacecraft exploring deep space; far beyond the solar system. The spacecraft should overcome sun's gravitaional field with great escape velocity. In order to be successful, the semi-major axis of orbit should diverge to $\infty$ , in other words, the escape velocity is equal to

$v_{\infty} = \lim_{a \rightarrow \infty} \sqrt{GM \left( \frac{2}{r} - \frac{1}{a} \right )} = \sqrt{\frac{2GM}{r}}$

5. Real Applications

Using information from last talk <Math & Physics #10>, $a = 149.6 \times 10^6 \text{ km}$ . The speed of revolution at apoapsis (minimum) is about

$v_a = 29,295 \text{ m/s},\ v_p = 30,290 \text{ m/s}$

hmm, not much difference considering the magnitude of speed isn't it? Also at the surface of the earth, the escape velocity respect to the sun's gravitational field is about

$v_{\infty, sun} = 41.78 \text{ km/s}$

slightly differs from real value $42.1 \text{ km/s}$ . The escape velocity resepct to the earth's gravitational field is theoretically,

$v_{\infty, earth} = 11.186 \text{ km/s}$

a perfect match with real value.

As you can see, due to mass difference, escaping from the sun is way more difficult than the earth.

6. Conclusion

Keppler's second law states that the line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
At any point, the cross product between position vector $\mathbf{r}$ and velocity vector $\mathbf{v}$ is constant.
Moreover, $\lVert \mathbf{v} \rVert = \sqrt{GM \left( \frac{2}{\lVert \mathbf{r} \rVert} - \frac{1}{a} \right )}$ holds.

I will finish this post with simulation of earth's revolution.

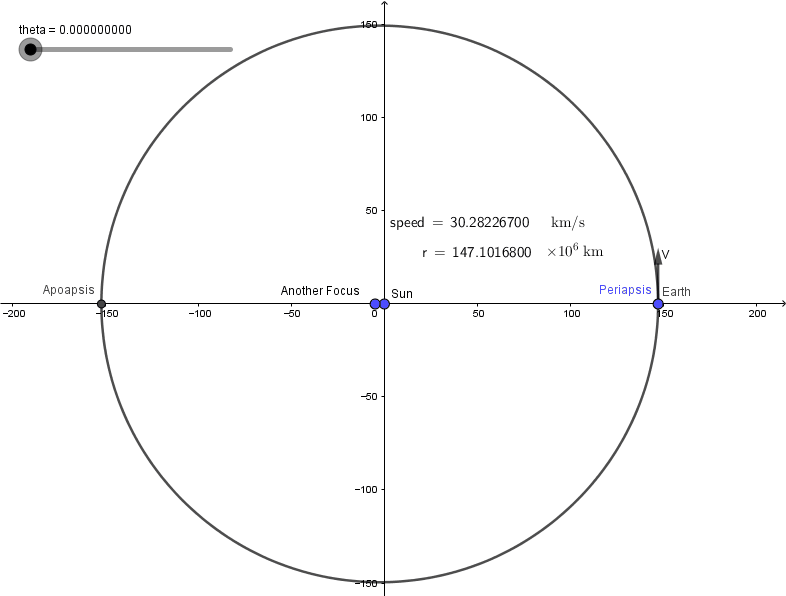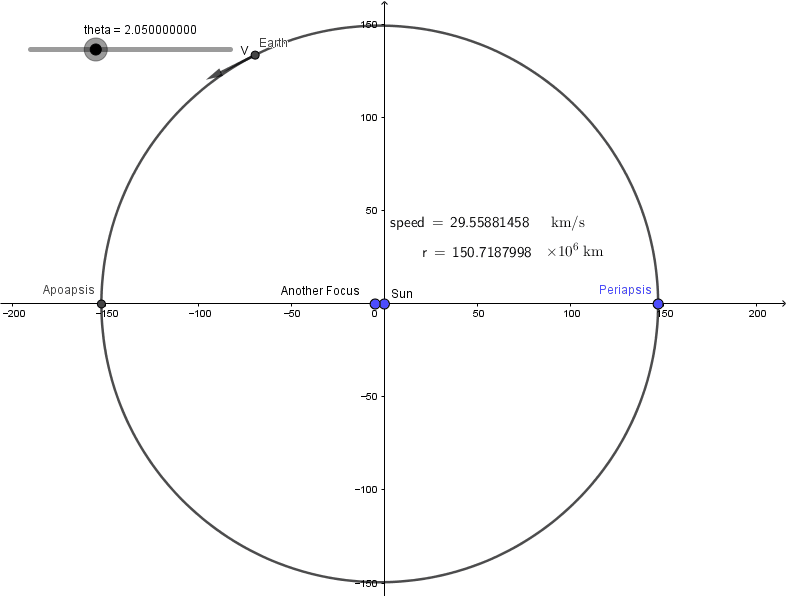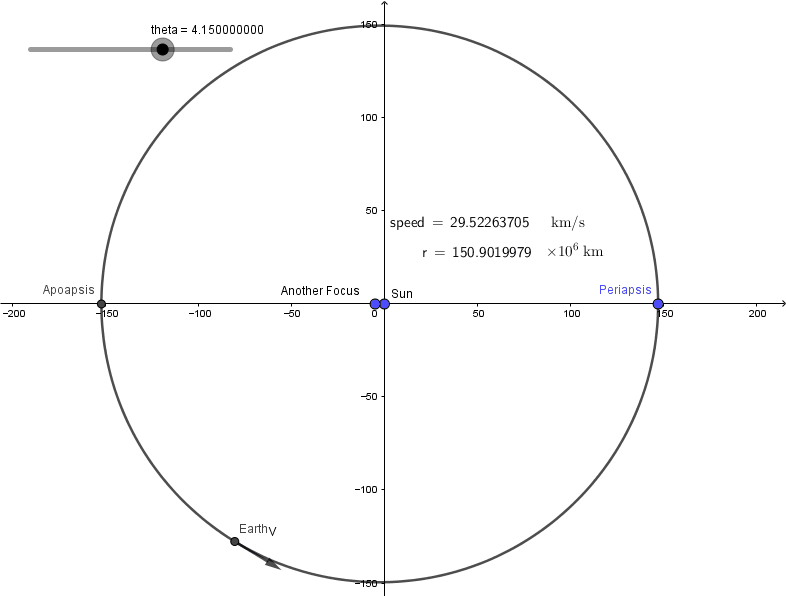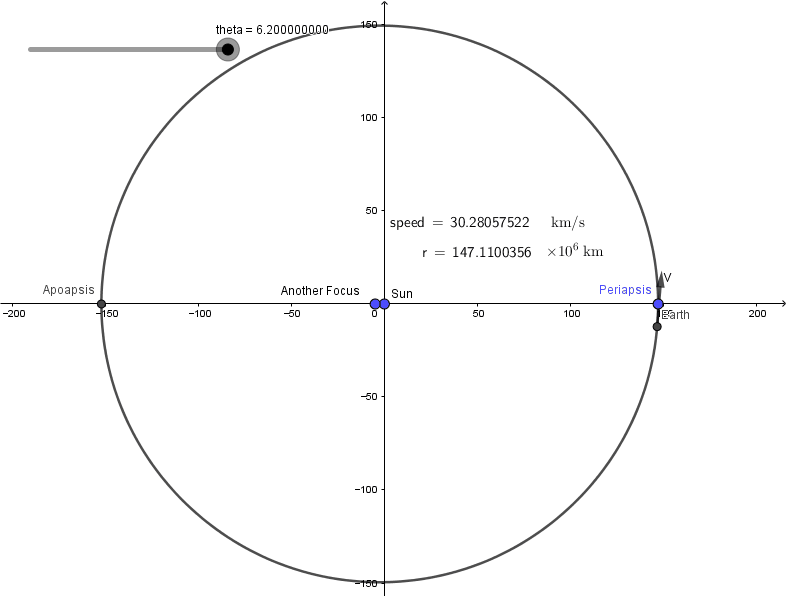
Can you see the difference? Well...not quite :(

7. Citations

[1] https://www.ck12.org/c/physics/keplers-laws-of-planetary-motion/lesson/Kepler%E2%80%99s-Laws-of-Planetary-Motion-PHYS/ (only image is used)

[2] https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion#Second_law_of_Kepler (gif)

[3] https://archive.org/stream/Astronomianovaa00Kepl#page/166/mode/2up

[4] https://books.google.co.kr/books?id=wa2SE_6ZL7YC&pg=PA668&redir_esc=y#v=onepage&q&f=false

[5] https://en.wikipedia.org/wiki/Vis-viva_equation

#physics #science #steemstem #mathematics

6 years ago in #math by mathsolver (53)

$4.17

Sort:

Trending

[-]

steemstem (73) 6 years ago

This post has been voted on by the steemstem curation team and voting trail.

There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!

$0.00

[-]

utopian-io (71) 6 years ago

Hi @mathsolver!

Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.

Contribute to Open Source with utopian.io

Learn how to contribute on our website and join the new open source economy.

Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV

$0.00

STEEM 0.18

TRX 0.16

JST 0.029

BTC 76570.32

ETH 3135.99

USDT 1.00

SBD 2.63