[1]

Kepler's Laws of Planetary Motion [Part 1] - Beauty of Ellipse

1. History

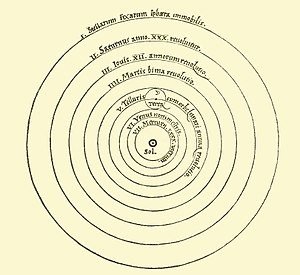
In the early stage of heliocentrism, it was widely believed that planets have pefect circular orbits.

[2]

Early heliocentrism postulated that

1. The sun is at the center of all orbits.

2. All planets revolve around the sun in uniform circular motion .

Even Galileo Galilei, the most famous natural philosopher in 16~17 th century believed that all planets have circular orbits.

---

It was not unil Johannes Kepler found three laws of planetary motion that people realized what orbits of planets really are. In 1609, Johannes Kepler published his first two laws about planetary motion, having found them by analyzing the astronomical observations of Tycho Brahe . Kepler's 3rd law was published in 1619. Kepler had believed in the Copernican heliocentric model of the solar system, which called for circular orbits, but he could not reconcile Brahe's highly precise observations with a circular fit to Mars' orbit—Mars coincidentally having the highest eccentricity of all planets except Mercury. His first law reflected this discovery which I will discuss about in this talk.

2. Ellipse Revisited in Polar Coordinates

2-1. Eccentricity and Directrices of an Ellipse

As we've discussed in previous talk, (<Math Talk #9>) an equation for ellipse having semi-major axis and semi-minor axis is

where are two focal points. Here we define two concepts called eccentricity and directrix.

---

Eccentricity of an ellipse is defined as

For an ellipse of the form (1), we have eccentricity .

Directrices of an ellipse are the lines perpendicular to the major axis at distances

from the center of an ellipse. Using diagram,

---

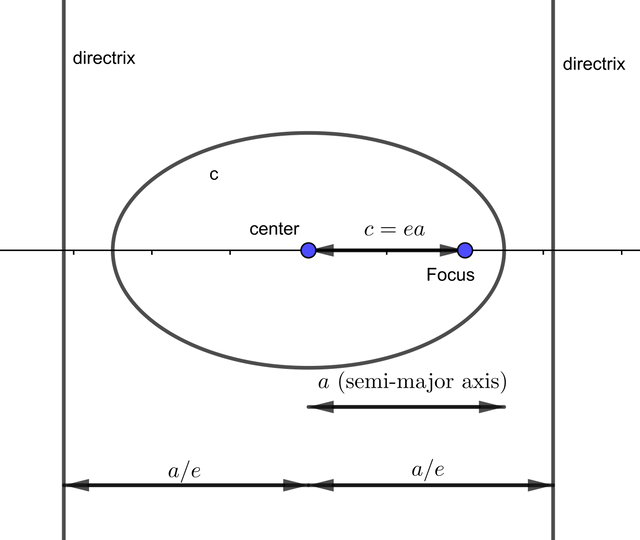
A simple algebra gives for any point on ellipse, , where is the perpendicular foot from to the closest directrix.

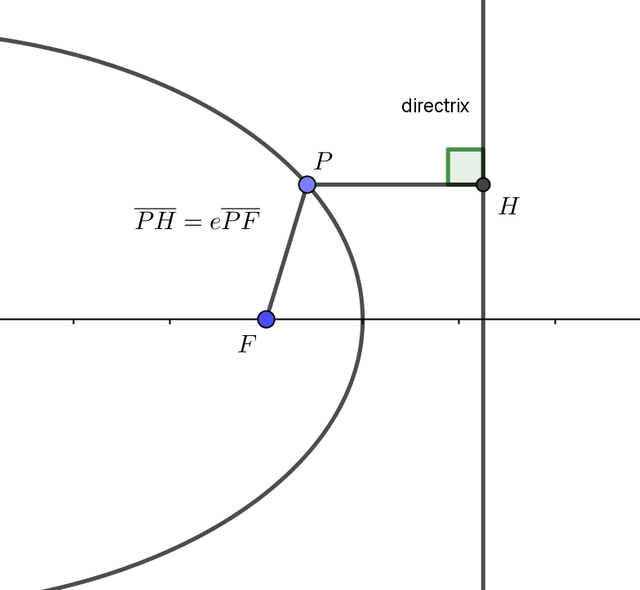
2-2. Using Polar Coordinates

Consider an ellipse having one focus at the origin with directrix .

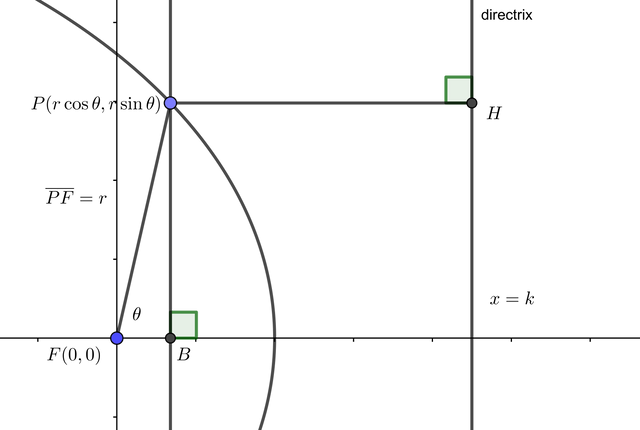
If we denote the perpendicular foot from to directrix as , then using diagram in section 2-1 gives

solving simultaneous equations give an equation of ellipse in polar coordinate,

3. Proving the Kepler's First Law of Planetary motion

Now all the background ingredients for proving first law of planetary motion are prepared.

---

Kepler's First Law of Planetary Motion.
The orbit of a planet is an ellipse with the Sun at one of the two foci.

---

First, we define some variables. [3]

1. : mass of the sun.

2. : mass of the earth.

3. : distance between earth and the sun

4. : Newton's gravitional constant

5. : angle between the positive x-axis and the line connecting earth and the sun.

6. : velocity vector of the earth

7. : radial and angular component of polar coordinate in earth's frame.

Locating the sun at the origin, we get the following diagram.

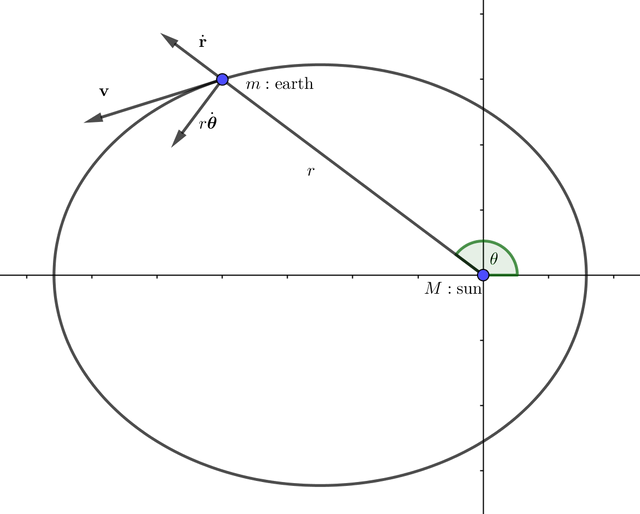
By the law of conservation of energy, the sum of potential and kinetic energy of earth is constant everywhere; i.e.

Decomposing the velocity vector in radial, angular component,

where dot denotes differentiation respect to time and . Also the angular momentum is given by

Now make substitution . Then , and

because . Combining energy equation and angular momentum equation, we have

where . Now put this equation into the integral, gives

using the fact . Then the equivalent form would be

The minus sign on the right side of the final equation just denotes whether the sun is located at left or right focal point, so it doesn't effect the shape of the orbit. Using the equation in section 2-2, we have a nice elliptical orbit of the earth!

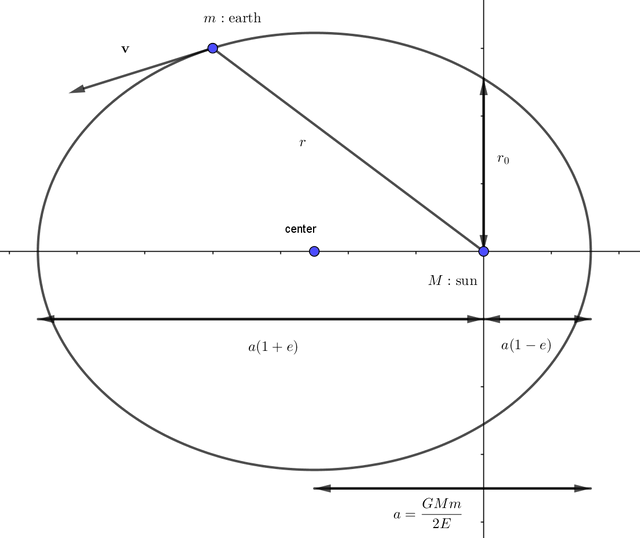
4. Actual Values considered

Actual values are measured by experiment or other analytical techniques. - [4]

1. Mass of the earth:

2. Mass of the sun:

3. Gravitational constant:

4. The apoapsis (maximum distance between sun and earth) is .

5. The periapsis (minimum distance between sun and earth) is .

So, the eccentricity of earth's orbit is

which is very close to circular orbit . This is why astronomers in 16~17th century believed the earth's orbit as circle; since there were no instruments which can measure such slight difference. Also the length of semi-major axis would be

The earth is rotating with total mechanical energy of

respect to the sun, which is way beyond our imagination~!

5. Conclusion

Although Kepler himself found three laws of planetary motion, at that time there were no precise mathematical foundations to prove them rigorously. It was Newton - the giant - who first proved three laws mathematically, using calculus. Nevertheless, Kepler's intuition (which was due to Tycho Brache's observations to be honest) was a great breakthrough in study of astrodynamics. Next time I will discuss about Kepler's second law of planetary motion.

I will end this post by real (not exaggerated) orbit of earth.

6. Citations

[1] https://www.intmath.com/plane-analytic-geometry/5-ellipse.php (only image is used)

[2] https://en.wikipedia.org/wiki/Copernican_heliocentrism (only image is used)

[3] http://radio.astro.gla.ac.uk/a1dynamics/keplerproofs.pdf (proof technique)

[4] https://en.wikipedia.org/wiki/Earth%27s_orbit#Events_in_the_orbit (orbital characteristics)

All the other materials (2D plots) are made by myself using GeoGebra.