[1]

Conic Sections - Ellipse

1. From Cone to Ellipse - The origin of Ellipse

In the last talk <Malk Talk #8>, we discussed about parabola; the line of intersection between a cone and a plane parallel to the generating line of the cone. Now the question is

How about a plane which is NOT parallel to the generating line of the cone?

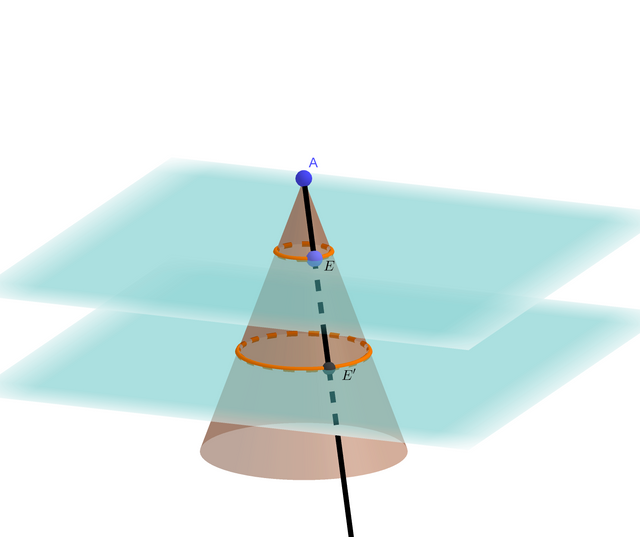
The following figure shows the line of intersection between such plane and the cone.

A nice, smooth closed curve shows up. How do we know that this curve is indeed a ellipse? To begin with, we need to know definition of an ellipse.

2. Definition of Ellipse

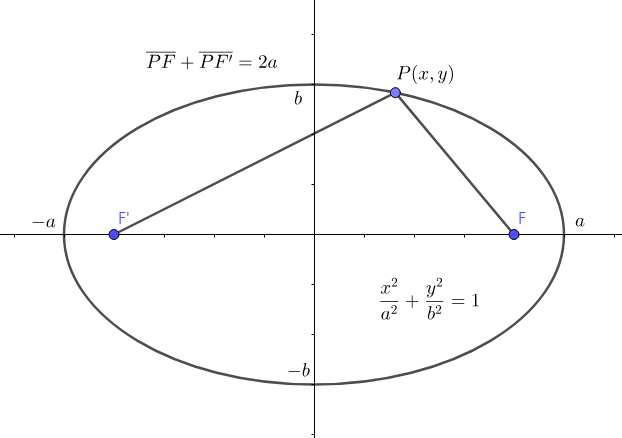
An ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve.

The animation shows the trace of a point satisfying

with two focal points .

If you do simple algebra, the equation of ellipse, having two foci with

is given by

where

3. Conic Section - Why is it an ellipse?

Well, using the above definition in Section 2, look at the following figure.

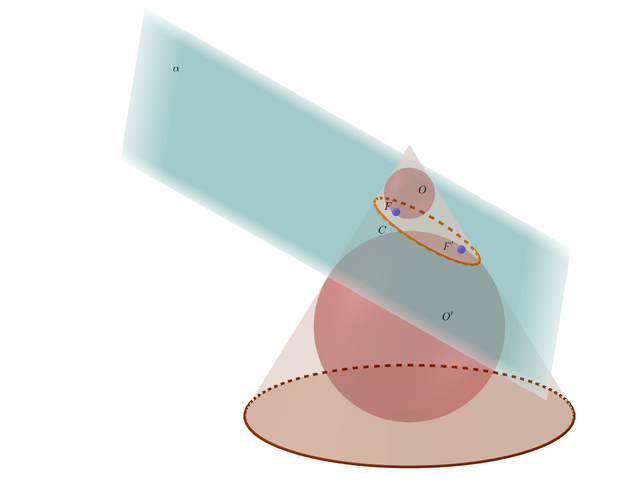
1. We define the intersecting curve between plane and the cone as .

2. Spheres , are the ones contact with both the cone and the curve .

1. We denote the point of contact where

1. Now denote a point on as . Denote the intersection between the ray and by .

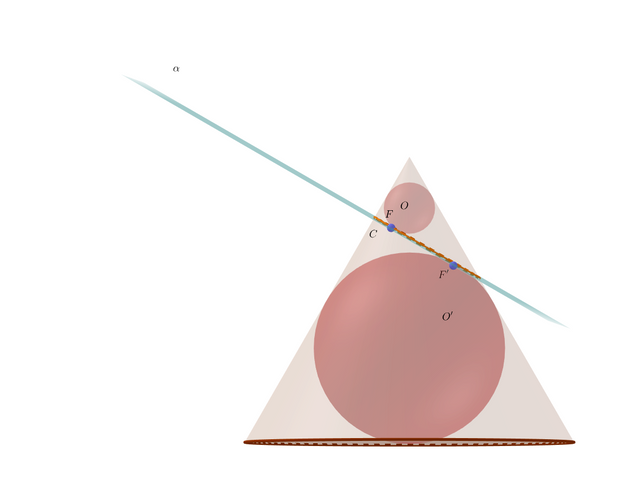
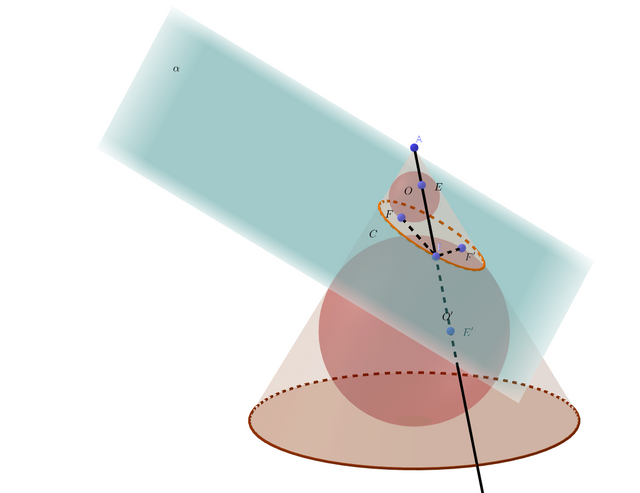
Then , and since the points are collinear, we get the fact

because

are all the same. So the curve , is indeed an ellipse.

3. Properties and Usages

Focal point to Focal point

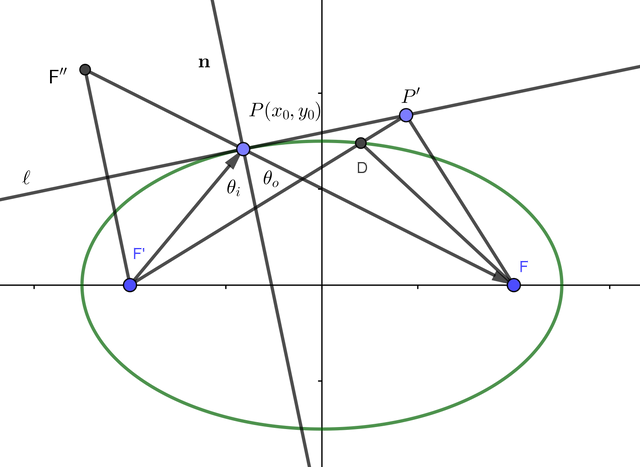
Consider a ray coming out from the focal point . What we are gonna prove is that the normal vector bisects the angle , so that .

Proof. -[2]
Let be the reflection of over the tangential line . Also pick another point on the tangetial line which is NOT . Then

using triangle inequality. So the sum of two segments any point which is not is always greater than the sum at . This implies that is the minimum, which then by law of reflection should be collinear. Thus .

---

So any light (ray) coming from one of the focal points of ellipse goes to another focal point when hit by any point on the ellipse. We can directly apply this fact to make an elliptical mirror,

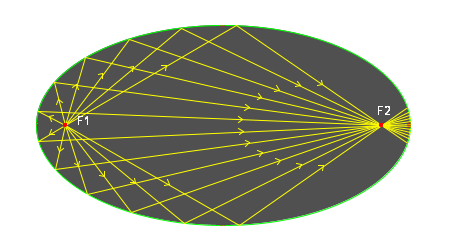
[3]

.

Medical Purposes

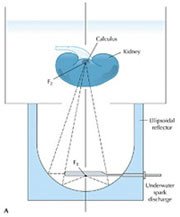
[4]

Suppose a patient has a cancer in his/her kidney. By locating his/her kidney on one of the focal point of the ellipsoid and the gammay ray emittor on the other focal point, you can concentrate all the gamma ray energy using the ellipsoidal mirror to the kidney; which greatly increases the efficiency.

Whispering Gallery

A Whispering Gallery is a room shaped like an ellipsoid, an ellipse in three dimensions, and is designed so that a whisper on one side of the gallery can be heard on the other. If two parties stands at each focal point, they will hear other group's voice more clearly, even if they are far apart.

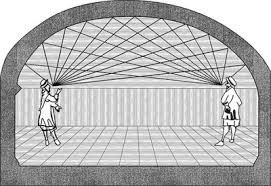
[5]

4. Conclusion

Ellipse & Ellipsoid can be used to concentrate lights, gamma rays, or acoustic sound by their inherent geometric property.

5. Citations

[1] http://www.deliu.ro/mod/wiki/view.php?pageid=19 (only image is used)

[2] https://terms.naver.com/entry.nhn?docId=2073855&cid=47324&categoryId=47324 (proof technique)

[3] https://www.mathopenref.com/ellipseoptics.html (only image is used)

[4] http://sev.iseverance.com/dept_clinic/department/urololgy/disease/view.asp?con_no=25122&page=&SearchField=&SearchWord= (only image is used)

[5] https://www.thewelcomeblog.com/stories-of-new-york/the-whispering-gallery-at-grand-central-terminal/4/28/2016 (only image is used)

All the other 3D plots as well as 2D plots are done by myself using GeoGebra 3D plotter and graphics calculator.