[math, computation] conformal map and conformal algebra //Feat Escher
Today i want to talk about conformal map and some computation on conformal algebra or conformal symmetry
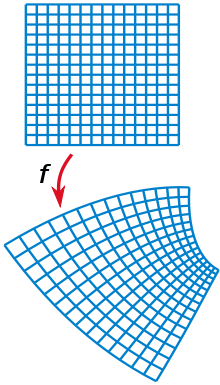
When you study complex analysis, by the end of the semester you might encounter the concept of Conformal map,. This map often be called angle-preserving map. By introducing some figures in wiki, you can see
The angle of rectangular which is right angle is preserved along the transformation. The simplest example of conformal map is scaling function.
Taking another examples, let me introduce some of masterpiece of Escher
I already used this figure in my previous post [math, computation] ADS geometry
You can see this has negative curvature. You can see devils or angels. By observing more in detail, by looking out for boundary, the figures becomes more smaller than its center.
How about flat curvature?, In this case the shape of figures are same whether it is located in center or boundary.
For positive curvature, Escher made this as a a sculpture
You can find this masterpiece in google by searching "Escher, devil and angles"
As an Dutch artist, he used geometry and mathematical principle in his works a lot. Especially this kinds of works of tessellations, he used symmetry of discrete groups such as reflection, glide reflection translation and rotation. So many of his works appear in abstract algebra textbook.
This conformal map often used as a tool for studying Riemann surface and its symmetry algebra, i.e., conformal algebra is another powerful tools in both mathematics and physics. In physics, this conformal concept is used in statistical mechanics, quantum field theories and string theories a lot.
Now let me introduce conformal algebra, and compute their relation explicitly for fun.
First introducing generators
where P, D, L, K stands for momentum, dilation, rotation and special conformal transformation.
The thing that i want to show is find the relation between these generators.
To prove this we first introduce test function, f and just do the computation by hand. Note if we neglect D and K, it is nothing but poincare algebra which governs quantum field theories. So in this sense qft is some limit of cft.
Mostly these kinds of things are left as an exercise at the end of the chapter. Here let's do it.
Starting from first relation
In this sense you can compute test function. Basically rest are the same. Here i provide my computation.
Colored term cancel out each other.... For cumbersome i forgot to type color......
Any way you can check the conformal algebra in this sense. It seems lengthy but it is nothing but adding and subtracting and re-organizing!




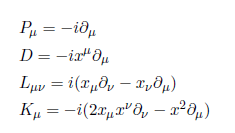


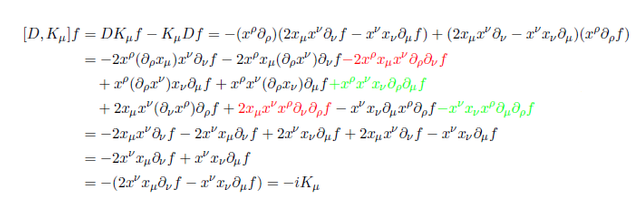


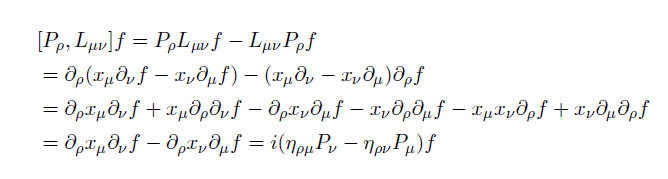
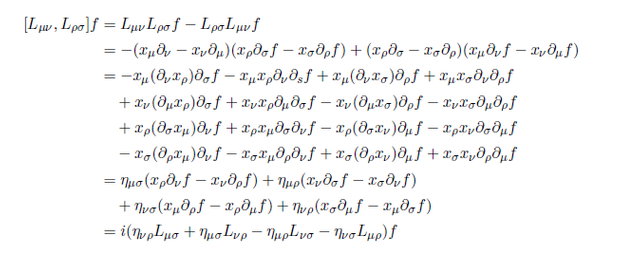
Congratulations @beoped! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPExcellent post