기하평균과 로그수익률
산술평균과 기하평균
산술평균은 길이(1차원)의 평균이며, 기하평균은 면적 및 부피(2차원이상)의 평균이다. 다른 말로하면 산술평균은 덧셈의 평균이며, 기하평균은 곱셈의 평균이다.
그림으로는 다음과 같이 표현할 수 있다.
한편, 산술평균과 기하평균은 다음과 같은 관계를 가진다.
그림으로는 다음과 같이 표현할 수 있다.
<산술평균은 파란색 삼각형의 높이, 기하평균은 주황색 삼각형의 높이>
밑변이 a+b인 직각삼각형(주황색)의 높이(
)는 "소"의 공식을 이용하여 산출할 수 있음. (이 부분을 몰라서 찾아봤는데 중학수학이었다는;;)
위의 그림에서 산술평균은 기하평균보다 항상 크며, a와 b가 같을때 산술평균과 기하평균이 같아진다는 것을 알 수 있다.
주지하다시피 누적수익률은 각기간의 수익률의 곱으로 계산되기 때문에 수익률의 평균은 기하평균을 사용하여 계산하는 것이 정확하다.
로그수익률
연속복리수익
먼저 연속복리 수익률에 대해서 알아보자. 연속복리 수익이란 (자연상수) er로 계산되는 수익률을 말한다.
자연상수 e는 다음과 같이 정의 된다.
또는
한편 수익률은 기간 수익률은 (1+r)로 표시가능하며, 해당 기간 동안 이자를 n번으로 나누어 받으면 수익률은 (1+r/n)n 가 된다. 이자를 무한대로 쪼개서 받으면 연속복리 수익인 er를 도출 할 수 있다.
연속복리수익
여기서 k = r/n으로 정의하면, n = r/k가 되어 다음과 같이 쓸 수 있다.
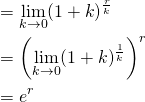
연속복리수익의 의미는 무엇일까? 복리수익은 이자에 다시 이자가 붙는 방식이므로 똑같은 이자율을 적용하더라도 이자계산을 자주 할 수록 실제 수익이 높아진다. 하지만 무작정 높아 지는 것은 아니며 최대 er까지만 높아질 수 있다.
예를 들어 연간 표시이자율이 5%일 때와 50%일 때를 살펴보자. 이자지급횟수가 늘어날때 마다 수익률이 증가하는 것을 볼 수 있으며, 수익률이 클 때 더 큰 폭으로 증가한다. 역으로 말하면 실제 수익률과 연속복리수익률의 차이(오차)는 수익률이 클 수록 커진다.
연속복리수익을 다기간으로 확장하기 위해서는 r대신 rt를 사용(즉, ert)하면 된다. 연속복리수익률을 가정하여 투자후 2배가 되는데 걸리는 시간을 계산해보자.
t기간의 연속복리 수익은 ert 이므로 수익률이 2배가 되는 시점은 다음과 같이 계산할 수 있다.
ert = 2
양변에 로그를 취하면,
rt = ln2 = 약 69.3%
t = 69.3%/r
72의 법칙
즉, 69.3%를 수익률 r로 나누면, 2배가 되는 기간을 구할 수 있다. 편의상 69.3%를 72%로 대체하여 쓰기도 하는데 이를 경제학에서는 "72의 법칙"이라고 한다. 72는 2,3,6,9 등 다양한 숫자로 나누어떨어지므로 계산의 편의상 72를 사용한 것으로 보인다.
여기서 주의할 점은 t를 계산할때 연속복리 수익을 가정하였다는 것이다. 따라서 실제 수익률을 적용한 t 기간과는 약간의 차이가 발생할 수 있으며, 그 차이는 수익률 r이 커짐에 따라 커지게 된다.
로그수익률
로그 수익의 중요성과 관련해서는 @jongsiksong 님의 글을 참고 하시면 됩니다.
로그 차트를 봐야하는 이유
재무에서는 계산과 비교의 편의성을 위해 로그수익률을 많이 사용한다. 로그의 특성을 이용하면 곱셈과 나눗셈을 덧셈과 뺄셈으로 바꿀 수 있으며, scale의 영향을 받지 않기 때문에 과거 수익률과 비교가 용이하다.
투자금액 Xt-1가 Xt로 증가(감소)했을때, 로그수익률(K)은 다음과 같이 계산된다.
로그수익률은 다음과 같이 일반수익률(r)로 변경할 수도 있다.
로그수익률을 그대로 사용하기
일반수익률과 로그수익률의 값은 다르게 계산 된다. 하지만 특정한 조건에서는 로그수익률을 일반수익률처럼 사용할 수도 있다. 어떤 경우일까?
로그수익률(K)가 일반수익률(r)과 같다는 것은 다음의 식이 성립함을 의미한다.
위의 식은 r이 "0"에 근접할때 성립한다. 증명은 테일러전개를 이용하여 가능하다. 즉, f(X) = ln(1+X)로 두고 1차항까지 테일러 전개를 하면 다음과 같은 결과를 얻는다.
<출처 : 시계열데이터에 로그변환을 취하는 이유>
즉, r = 0에 근접할 때 일반수익률(r)과 로그수익률(K)가 유사하므로 이를 활용하여 쉽게 수익률 등을 계산할 수 있다.
기하평균과 로그수익률
최초 투자액 X, 1기간수익률 a, 2기간수익률 b인 경우의 기하평균(GM)과 로그수익률 평균(LM)을 계산해보자.
기하평균에 로그를 취하면,
기하평균에 로그를 취한 값은 로그수익률의 평균과 같다는 것을 알 수 있다.
글이 맘에 드신다면 아래 광고를 클릭해주세요~ 힘이 됩니다^^
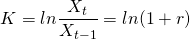
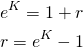
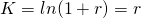
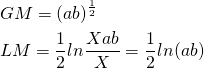
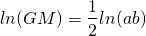

와우. 대단하세요 ~
학생때 안하던 공부가 이제 좀 재밌어져서 조금씩 하고 있습니다^^
눈이 빙글빙글 ^^;
저도 그렇습니다^^;
하하 이걸 어떻게 풀죠 덜덜 숫자는 치과보다 무섭네요
치과는 비용이 무섭죠^^
고등학교 1학년때 배웠던 것 같은데, 가물가물 하네요. @_@
기억력이 좋으시네요~
저는 배운기억도 없습니다^^
자고 있었나봅니다;;
한글...맞나요..? ;ㅅ;
중간에 한글이 있긴합니다.^^;;
Hi @thrufore!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 0.211 which ranks you at #84562 across all Steem accounts.
Your rank has not changed in the last three days.
In our last Algorithmic Curation Round, consisting of 298 contributions, your post is ranked at #225.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server
중학수학 소의 공식 h2 = ab가 왜 이렇게 되는지 모르겠네요. ㅎㅎㅎㅎ 그냥 외웠군요. ㅋㅋㅋ 과외는 신인데 도대체 애들한테 뭘 가르친건지 ㅋㅋㅋ
닮은 꼴을 이용한다네요. 저도 중학교때 배운 기억이 없는걸보니 그냥 외운듯 합니다^^ 지금 생각해보면 수학교육의 현실이 좀 안타깝기도합니다 ㅎㅎ
저는 제가 가르쳤는데 ㅇ_ㅇ 쫌 미안해집니다. ㅋㅋㅋㅋ
과외선생님에게 기대하는건 빠른 시험점수의 향상이니 미안해하지 않으셔도 될듯 합니다. ㅎ
그거야 기본이죠. ㅇ_ㅇ;; 선생인 이상 수학에 도통하게 만들어야죠.
가르치는 자존심이 있지 않겠습니까 ㅋㅋㅋ
저도 수학을 못하는 편인데, 뒤늦게 관심을 가지려니 힘드네요~ 저에게도 가르침을 주셔서 도통하게 만들어주세요^^
헐 그렇군요. ㅇ_ㅇ 수학은 세계에서 제일 쉬운 과목입니다. ㅎㅎㅎ 예. 기회 될 때 조금씩 알려드리겠습니다. ㅎㅎㅎ 오홋 도통 목표라니 대단하심 ㅋㅋㅋㅋ
짱짱맨 출석부 호출로 왔습니다.
감사합니다~짱짱맨 응원합니다^^
1004데이 ^^ 짱짱맨 출석부
그랬네요, 모르고 있었습니다^^
아직 Payout 되지 않은 관련 글
모든 기간 관련 글
인터레스팀(@interesteem)은 AI기반 관심있는 연관글을 자동으로 추천해 주는 서비스입니다.
#interesteem 태그를 달고 글을 써주세요!