[수학, 계산] 리만기하 4 -metric 변분법 // 응용-Low-energy effective action - part 2
지난번 포스팅에는 운동방정식 유도에 필요한 수식들을 유도해 보았다. 사실상 리만기하의 변분 공식 유도라고 해도 무방하다. 지난번에 증명한 수식들을 바탕으로
의 equation of motion 을 구해보자
자 저 action 은 phi, B ( 저 식의 H=dB 이다), metric G 로 구성되어 있기에, 각각의 경우에 따라 변분해 주면 된다.
B 로 변분
먼저 B 에 대해서 변분해 보자.
B에 대해 변분하기 전에 H 의 정의를 서술해 보면
간략하게 H=dB 로 쓰기도 한다. 여기서 저 two-form B field 는 anti-symmetric 하다. 즉
이를 이용해 H 를 explicitly 하게 써보면
자 B 에 대해서 변분해 보자
첫번째 식은 H^2 을 변분하는 과정에서 나왔고 첫번째에서 두번째로 가는 과정에서는
식이 쓰였다. 그리고 마지막 과정에서는
식이 쓰였다. Connection 의 symmetric 성질과 H 가 totally anti-symmetric 하다는 것을 이용하였다.
즉 이로써
를 얻고 divergence 형태를 이용하여
up to total derivatives
즉 이 식을 가지고 B에 대한 beta 함수 형태를 찾을 수 있다.
스칼라 Phi
Phi 에 대한 변분은
여기서
관계식이 쓰였다. action 형태로 살펴보면
즉
beta 함수의 정의를 불러와 보면
저 식은 다름이 아니라
metric G 에 대한 변분
먼저 G에 대해서 변분해 보면
일단 이 식을 얻기 위해서
자 이제 계산을 더 이어가기 위해서
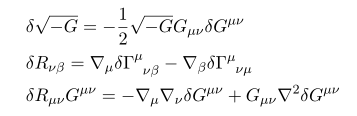
를 이용해 \delta G^{\mu \nu} 로 묶어 보는 작업을 해보자.
특별히 문제가 될 식은
으로
에 total-derivative term 들을 0으로 보내는 것으로 얻을 수 있다.
이제 결과들을 대입하여 정리하면
즉
첫번째 식은 Phi 에 대한 equation of motion 이라는 것을 쉽게 알 수 있다. Beta 함수의 정의를 불러와 다시 적어 보면
summary
지금까지 구한 운동방정식을 정리해 보자
저 식을 연립해 보면
좀 길었나? ㅎㅎ
저기에다 fermion matter 나 Higgs scalar field, 혹은 다른 additional 한 scalar field 를 추가해서 새로운 모델을 만들거나 현상을 파악하는 일들을 할 수 있다.

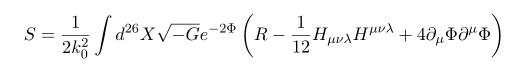
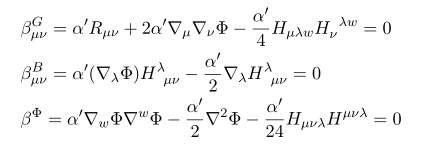
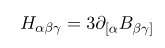
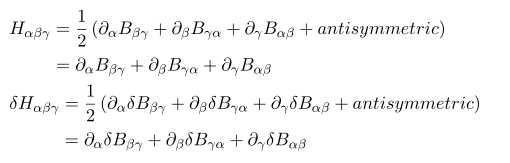
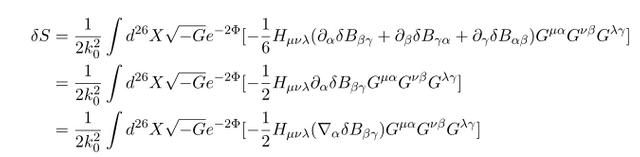
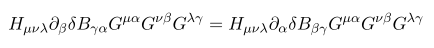
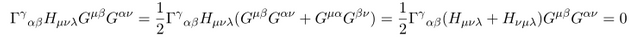
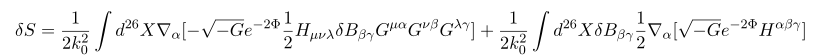
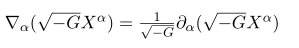
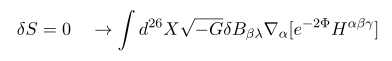
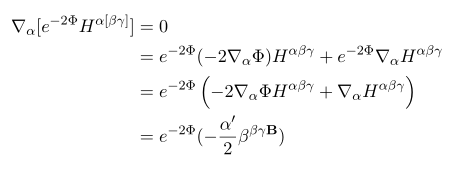
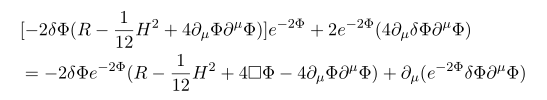
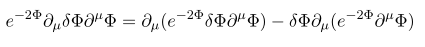
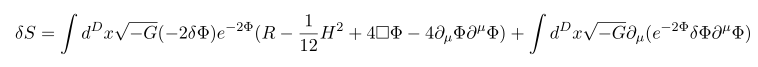
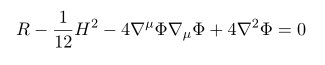
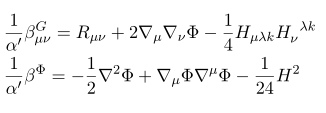
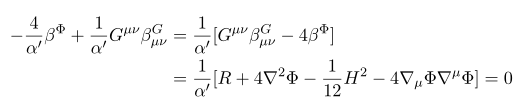
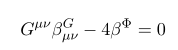
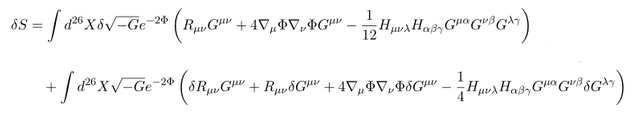
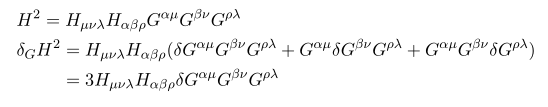
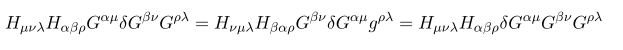
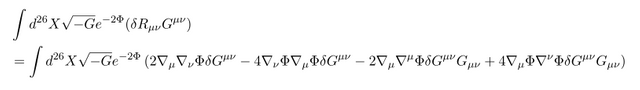
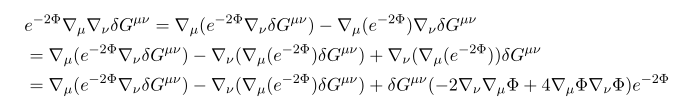
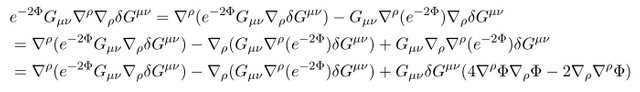
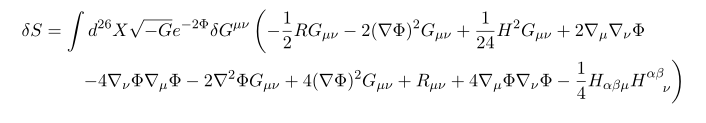
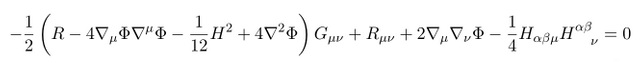
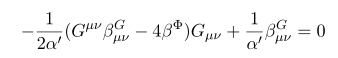
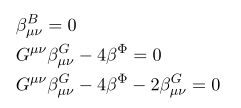
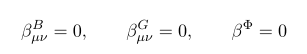
Cheer Up!
아주 유용한 게시물, 감사 합니다 공유, 이것은 정말 매우 창의적인 @beoped
수학 공부를 손땐지 한참 오래지만,
덕분에 다시 수학공부를 하게 됩니다.
기초가 부족해서 어렵지만, 최대한 이해해보려고 노력중입니다 ,ㅋ
ㅎㅎ;; 계산을 제대로 이해하려면 학부 혹은 대학원 수학과의 미분기하나 리만기하학, 혹은 물리학과의 학부 혹은 대학원 상대론 내용이 필요해서요... ㅠㅠ
그냥 이런 계산도 있구나 하시면 될거에요 ㅎㅎ
천재네요
천만에요 제가 한 것은 그냥 연습문제 풀이에 불과합니다;; 사실 물리쪽 접근에서는 equation of motion 도 중요하지만 저 low-energy effective action form 자체의 중요성을 많이 봅니다. 맨 처음 저 action form 을 생각해낸 사람이 천재겠지요....
후대 사람은 저 action을 보고 그냥 단순 계산을 하면 되니까요 ㅎㅎ.. 물론 계산이 뚝딱 나오지는 않지만요 ㅠㅠ
아인슈타인 역시 자신의 운동방정식을 만족하는 action을 찾기 위해 엄청 고생했었고 여러 시도 후에 R 을 찾았지요. [사후에 공개된 아인슈타인의 노트에 여러 시도 등이 공개되었죠 ㅎㅎ] 힐버트도 여기에 관심이 있어서 action 을 찾았고 이 action 이 Einstein-Hilbert action 이에요 ㅎㅎ
연습문제 풀이 수준이라고 말씀하시는게 겸손이라도 믿기 힘든걸요 ㅎㅎ 아무리 그래도 이론물리 전공자가 아니라면 거의 이해하기 힘든 내용이니까요