Buongiorno a tutti cari amici, benvenuti al primo "corso" di fisica su Steemit,

Scrivo "corso" tra virgolette perchè non ha come obiettivo principale quello di formare dei fisici ovviamente, non ne sarei in grado. Come diceva uno dei miei docenti, cito testualmente:

"Quelle quattro cazzate che vi insegnamo durante questi cinque anni di studi non faranno di voi dei fisici, vi forniranno appena gli strumenti necessari a leggere un vero libro di fisica"(M.P.)

Il mio obiettivo è quello di mostrare ai "profani" del settore come funziona questo meraviglioso strumento, frutto di secoli di studi, e quali sono le dinamiche fondamentali che lo regolano, tramite esempi ed esercizi, fornire argomenti su cui riflettere e mettere a disposizione di tutti quello che ho imparato. Cominceremo dall'inizio, quindi in particolare focalizzeremo la nostra attenzione sulla:

Meccanica

Immagine libera da copyright.
Fonte

La meccanica, è la branca della fisica che si occupa del moto di un corpo, e delle relazioni che questo moto ha con le cause che lo producono, essa si divide ulteriormente in due campi di studio:

Cinematica: è la descrizione del moto come fenomeno spaziotemporale.

Dinamica: è lo studio del moto dei corpi in relazione alle cause che lo determinano.

Cominceremo introducendo la cinematica, mostrando le grandezze fisiche: posizione, velocita’ e accelerazione che servono a descrivere il moto dei corpi. Dopodichè passeremo alla dinamica e vedremo le leggi che connettono queste grandezze cinematiche alle cause del moto, ossia le forze.

Il caso più semplice di moto si ha quando è possibile schematizzare il corpo in movimento ad un punto materiale, ossia quando la dimensione del corpo in movimento che vogliamo studiare risulta trascurabile rispetto alla precisione con cui ci interessa localizzarlo. Esempio:

Un aereo nel cielo
In questo caso, essendo la dimensione dell'aereo trascurabile rispetto a quella dell'intero cielo, si può trattare il moto dell'aereo come se fosse un punto materiale.

Immagine libera da copyright fonte

Un aereo in un hangar
In quest'altro caso invece, essendo le dimensioni dell'aereo non trascurabili rispetto a quelle dell'hangar, non si può procedere alla schematizzazione di cui sopra.

Immagine libera da copyright fonte

Quando utilizziamo la schematizzazione di un corpo a punto materiale, "facciamo finta" che tutte le parti dell’oggetto si muovano nello stesso modo, vengono trascurati cioe’ i moti interni e le rotazioni, cose leggermente più complicate che arriveremo a vedere tra una decina di lezioni. Cominceremo dalla cinematica di un punto materiale, ossia l'introduzione di quelle grandezze fisiche che sono necessarie alla descrizione del moto di un corpo schematizzabile come punto materiale. Cominciamo:

Prima definizione: Traiettoria di un punto materiale

Essa è definita come il luogo delle posizioni occupate successivamente nel tempo da un punto materiale e generalmente è una linea retta o curva nello spazio, ad esempio la traiettoria della Terra intorno al Sole è ellittica:

Immagine creata con paint

Tuttavia la forma della traiettoria dipende dal sistema di riferimento in cui si trova l'osservatore (colui il quale osserva il fenomeno) ed è per questo che per secoli si è creduto che fosse il sole a ruotare attorno alla terra e non viceversa.. considerate il seguente esempio: Se il buon @marcodobrovich sta scrivendo le affascinanti storie di Gerardo (che vi invito a leggere perchè sono davvero bellissime) comodamente seduto su un frecciarossa che viaggia a 150 Km/h, ed io sono seduto accanto a lui, dal mio punto di vista, quindi nel mio sistema di riferimento egli è fermo, però se qualcuno, magari bevendo un caffè al bar interno della stazione, lo vedesse scrivere sul treno che passa, lo vedrebbe muoversi a 150 Km/h e vedrebbe un moto sviluppato su una linea di questo tipo, dova A è il punto in cui comincia a guardarlo e B il punto dove smette e torna al suo caffè:

Immagine creata con paint

Gradi di libertà

Se il nostro punto materiale è vincolato a muoversi su di una linea retta (come nell'esempio di Marco sul treno visto dal tizio al bar), un solo parametro è sufficiente a descrivere il suo moto:

Dove:
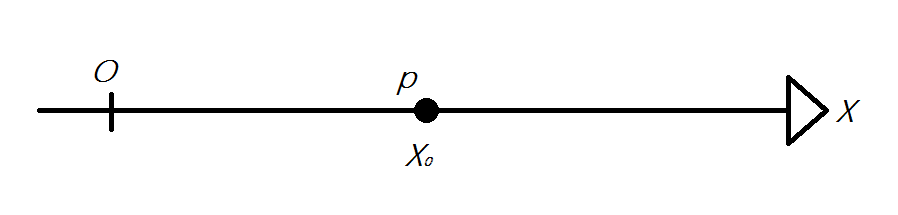
p = punto materiale
O = origine del sistema di riferimento
X = parametro con cui si localizza il nostro punto materiale (la retta su cui è vincolato a muoversi)
X0 = posizione di p in un determinato istante

In questo caso si dice che il punto materiale ha un grado di libertà

Se invece il nostro punto materiale è vincolato a muoversi su di una superficie, serviranno due parametri per determinare la sua posizione. Prendiamo ad esempio una palla su un tavolo da biliardo che possiamo schematizzare come segue:

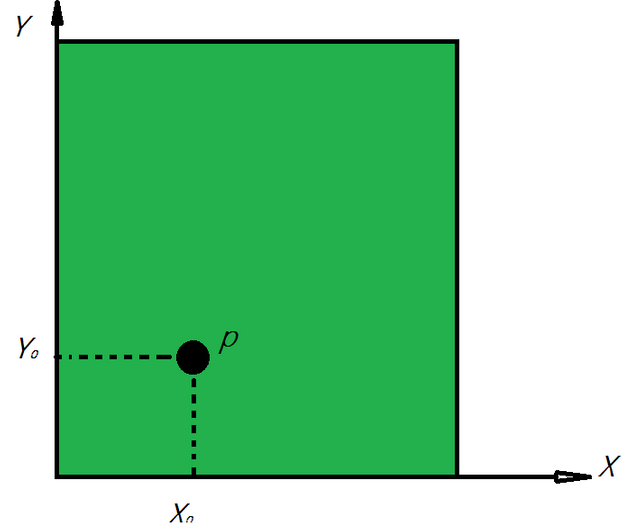
In questo caso il nostro punto materiale (la palla da biliardo) potendosi muovere liberamente in due dimensioni, lunghezza e larghezza, necessita due parametri per essere localizzata X, e Y, di cui X0 e Y0 rispettivamente sono le posizioni ad un certo istante, sul'asse della larghezza del tavolo (X) e su quello della sua lunghezza (Y)

In questo caso si dice che il punto materiale ha due gradi di libertà

E siccome non c'è due senza tre, se il nostro punto materiale fosse per esempio un aereo che si muove libero nel cielo, avrebbe bisogno di ben tre parametri per essere localizzato, se infatti schematizziamo l'aereo così:

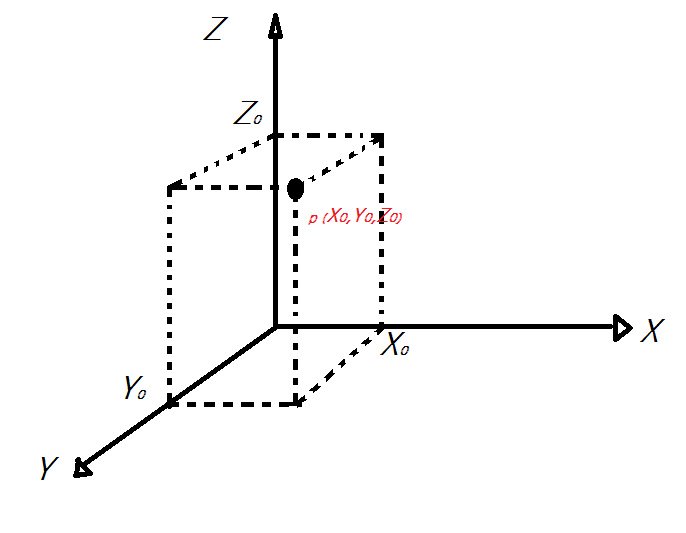
Vediamo che oltre a muoversi in lunghezza (X) e in larghezza (Y) dobbiamo determinare anche la sua altezza (Z), e quindi il nostro punto p, per essere localizzato dovrà essere definito tramite tre parametri, in questo caso si dice che il punto materiale ha tre gradi di libertà.

Ora, andiamo a vedere il moto più semplice nel dettaglio: Il moto di un punto materiale lungo una linea retta:

Posizione

Se il moto avviene in una sola dimensione, essa si può pensare come una linea retta (asse X) con un'origine (O), se prendiamo il primo esempio:

vediamo che il nostro punto materiale p occupa, in un certo istante (chiamato t0), la posizione data dalla coordinata X0. Se il nostro punto ha cominciato a muoversi lungo il percorso della linea retta, all'istante t = 0, la sua posizione negli istanti seguenti è data da:

x = x(t)

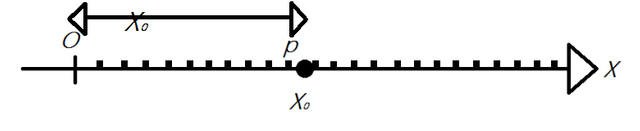
Che è una funzione di x, chiamata legge oraria del moto (o equazione parametrica). Questa funzione non è altro che una relazione che collega ad ogni istante t > 0 (ossia ad ogni istante successivo a quello in cui il corpo comincia a muoversi) una posizione ben precisa sul nostro asse X (la linea che segue il corpo durante il suo moto).

Grazie a questa legge oraria possiamo andare a fare già i primi calcoli, i più semplici, vediamo infatti la:

La velocità è la grandezza fisica che sta ad indicare quanto si muove rapidamente un corpo. Essa da un resoconto quantitativo del fatto che, nello stesso tempo, se ci sono due corpi che si muovono nella stessa direzione, il corpo che si muove piu’ rapidamente percorre uno spazio maggiore. Consideriamo il moto di una pallina che si muove lungo l’asse X, essa, all’istante t1 occupa la posizione X1 e all’istante t2 la posizione X2. Possiamo allora definire la Velocità media, nell'intervallo di tempo t1,t2 nel modo che segue:

Dove:

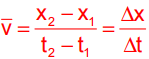
ΔX è uguale alla differenza tra X2 e X1 (quindi lo spazio percorso nell'intervallo di tempo)
Δt è uguale alla differenza tra il tempo finale e il tempo di inizio del moto (il tempo in cui è stato effettuato tutto il moto). In parole povere è il rapporto tra lo spazio percorso e il tempo impiegato a percorrerlo.

Ma spingiamoci un pochino più in la e andiamo a vedere cosa succede matematicamente, osserivamo questo grafico:

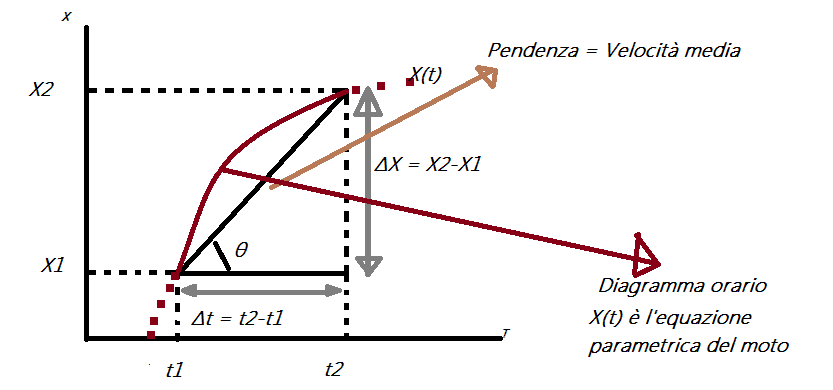
Considerato che il tempo scorre di secondo in secondo nella stessa direzione, ossia, l'istante in cui state leggendo il primo adesso viene prima dell'istante in cui leggete il secondo adesso, possiamo considerare t2 (l'istante in cui finisce il moto) > (maggiore) di t1 (l'istante in cui il moto comincia). Tenuto conto di questo e del fatto che la velocità media è definita come lo spazio percorso diviso per il tempo impiegato a percorrerlo, possiamo vedere che:

SE ∆X > 0, ossia se la differenza tra la posizione finale del corpo in moto (X2) e la posizione iniziale dello stesso (X1) è positiva, avremo un moto positivo verso la direzione delle X crescenti (in pratica la posizione del nostro punto andrà avanti)

Se sto giocando una partita di calcetto, e do una pedata al pallone calciandolo verso la porta dei miei avversari, dal mio punto di vista il pallone va avanti, perchè la sua posizione finale rispetto all'origine (la mia porta) è più distante dalla mia porta di quanto lo fosse prima di calciare il pallone, e quindi la sua velocità media (rispetto al mio sistema di riferimento) sarà positiva.

SE ∆X < 0, ossia se la stessa differenza tra la posizione finale del corpo in moto (X2) e la posizione iniziale dello stesso (X1) è negativa, avremo un moto negativo, verso la direzione delle X decrescenti, (in sostanza la posizione del nostro punto andrà indietro)

Consderiamo sempre la partita di calcetto: se anzichè essere io a calciare il pallone fosse uno dei miei avversari, il pallone si muoverebbe verso la mia porta, quindi andrebbe indietro rispetto all'origine (la mia porta) avvicinandosi ad essa più di quanto non lo fosse già prima di essere calciata.

Nel caso invece in cui il nostro punto terminasse il moto nella stessa posizione da cui è partito, ossia X1 = X2, la velocità media sarà uguale a zero, poichè lo spazio percorso sarebbe nullo, quindi uguale a zero, e zero diviso qualunque intervallo di tempo, darà sempre e comunque zero, e quindi la velocità media del pallone (rispetto al mio sistema di riferimento) sarà nulla.

Esempio assurdo: se durante la stessa partita dessi un calcio al pallone, e questo grazie ad una folata di vento tornasse esattamente nel punto in cui lo ho calciato, tecnicamente è come se fosse rimasto fermo, e non avvicinandosi alla mia porta, nè allontanandosi, la sua velocità media risulterebbe essere zero.

Ok, per essere una prima introduzione mi pare di aver messo già abbastanza carne al fuoco, riflettete su questo, e se vi fa piacere lasciate un commento, così saprò di non scrivere a vuoto (spiegare non è così facile come sembra XD) e se avete domande di qualunque genere chiedete pure, io sono qui :)

Mazzoldi, Nigro, Voci: Elementi di fisica 1: Meccanica
Focardi, Massa Uguzzoni: Fisica generale: Meccanica e termodinamica

Alla prossima "lezione" cari amici,

Logo creato da @mrliga

Dove non espressamente espresso, le immagini sono di proprietà dell'autore

Le "lezioni" avranno cadenza settimanale, perciò ogni GIOVEDI' (probabilmente sera) pubblicherò un post. Tuttavia, se molti dovessero interessarsi all'argomento potrei prendere in considerazione l'idea di pubblicare con più frequenza