Numbers in Game development | Part 2

Hi!, I am Adam Saudagar, this is the second part of the blog series “Numbers in Game Development” if you haven’t seen the previous one, I highly recommend to do so, link is below
Numbers in Game development | Part 1
Part 2
Maths functions, Whaaaat?

lets see what happens if we change this equation a bit, replace 4 with x and make that equal to y
This is known as exponential function, what does it mean then? It simply means that, if you want the answer to become 16 like before then we have to plug in x = 4,
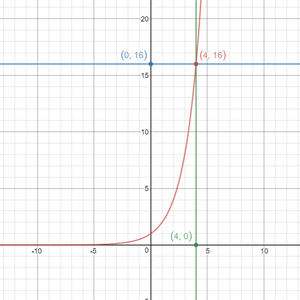
I am growing Exponentially :D

By trying the graph yourself, you might have noticed that as the value of x increases, not only y increases, but the rate of which y increases also increases. If you don’t understand this sentence, compare the exponential graph with linear graph, click the graph to try it out
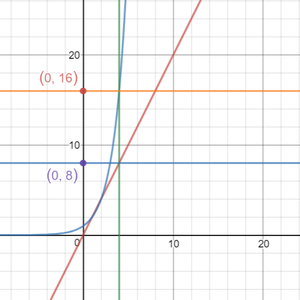
Rise my zombies
As I told you before, looking at just the maths will confuse anyone, but when we see the maths working in a game, we will understand how these maths functions work. So lets see how we will implement this maths in the game. First I will show you how the game works with a constant frequency of zombie spawning, then we will use linear growth function to understand how the variables in the game and maths variables links. And then we will implement our exponential growth function. Piece of cake, isn’t it?
The undead variables

Lets just see what are the variables we will use
- killCount (c) : this is the number of zombies we killed from the start
- spawnFrequency (f) : this shows how many zombies will spawn in the map in 1 second, this is what we want to increase exponentially with respect to killCount
- spawnIncreaseRate (r): this is the rate by which spawnFrequency increases
- initialSpawnFrequency (fi) : this is the spawnFrequency in the start of the game
- finalSpawnFrequency (ff) : this is the maximum value for spawnFrequency. We are keeping this because we don’t want our player to get destroyed by crazy amounts of zombies LOL
- killCountThreshold (cf) : this is the threshold amount of kills after which frequency becomes constant.
Enough with the boring stuff

Yeh, I know this has been boring enough, lets just see how the game works right now, with constant spawnFrequency.
I know the frequency is constant, but just to visualize it, lets plot a graph of killCount vs spawnFrequency, to have a better understanding of the situation
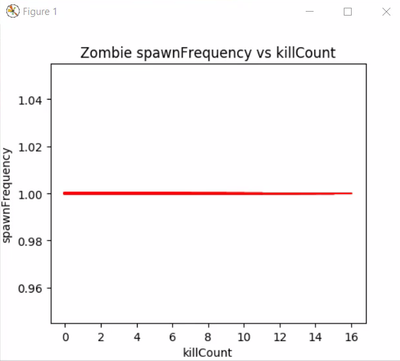
As you can see, for any value of killCount, spawnFrequency stays the same. We don’t want that. So how do we want it to be?
Growing linear
What we want to do is, increase zombie spawnFrequency as the killCount increases, lets try to make a rough graph for it.
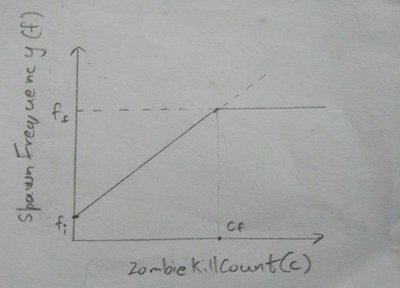
In the graph, we can see that when killCount is 0, the spawnFrequency is fi, that means in the start of the game when the player doesn’t have any kills, spawnFrequency will start at fi. We can see that from fi to ff the graph looks like a line, so we can plug in equation for line, which is
Lets check it out in desmos and see how it looks, click the equation above, try changing m and c to see how it effects the graph.
We were dealing with the variables we defined earlier, but what are these new variables, y, m, x, c. By simply comparing the graph we drew and the graph in desmos we can see that, y represents the Y-axsis, which is spawnFrequency. x represents the X-axis which is killCount. m represents the rate at which y increases, this also known as gradient in mathematics, that is spawnIncreaseRate. And c is called y-intercept in mathematics, which means the point on y axis where the line cuts or the value for y when x is zero. Hence c = fi. So writing the equation in terms of variables we are using for the game we get
looking back at our graph, line just goes from fi to ff after that the frequency stays at ff so
if
if
Coding It Linearly

We have finally calculated the equation for spawnFrequency but we can’t simply plug these formulae in the code. First we’ll have to decide what we want to adjust manually and use those to calculate rest of the formuales.
The varables we’ll need to enter manually are initalSpawnFrequency (fi), finalSpawnFreqency (ff) and spawnIncreaseRate (r). We will get killCount (c) from the game itself, as the player kill enemies killCount will increase. And as for f, we calculated the formulae in the previous section. Only variable left to calculate is cf. To calculate cf, what we will have to do is plug the point (cf, ff) into the equation (
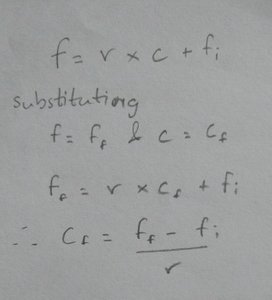
Watching it work (Linear)
So the equation we got is
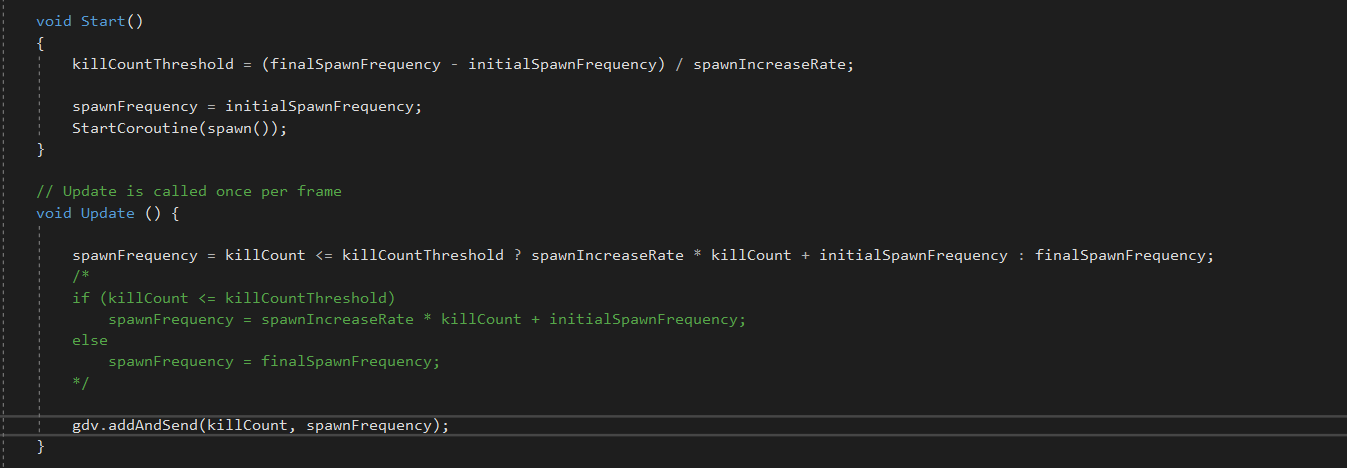
When the game executes, Start() fuction runs once then, Update() function loops for each frame. In the Start() function, first we use the killCountThreshold formula that we calculated,
then we initialized spawnFrequency to initialSpawnFrequency,
then we start spawning process by calling StartCoroutine(spawn()).
The first statement in Update() function is called Ternary operator, its synatx it,
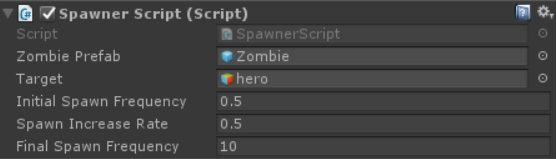
when the condition is true, result will be assigned to exp1, if the condition is false, result will be assigned to exp2. This statement will work as same as the code which is commented. We use this for the equations of spawnFrequency. Then we give custom values for the initalSpawnFrequency= 0.5, spawnIncreaseRate=0.5, finalSpawnFrequency=10.
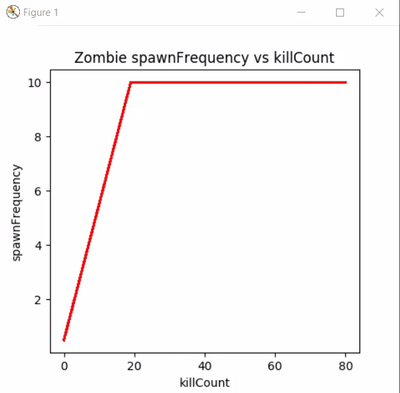
As you can see, we can literally visualize the graph that we calculated by maths into the game itself. This is the beauty of mathematics.
In the next part we will make it so the spawnFrequency grows exponentially instead of linearly, Thanks for reading my post, follow me to stay tuned for upcoming parts, and don’t forget to press the like button. I’ll see you guys later.
Squad fam out!
you put in a lot of effort! take my upvote :)
i would recommend you post your articles on utopian-io ( you can get extra rewards [I got 25$ :)])
what is utopian-io?
Just visit utopian.io
I joined utopian-io the other day, but felt that my tutorials wouldn't be right on there; given I'm trying to write a commerical game, thus my content isn't open source, am I right Wil1liam???
You're right
lol thanks :D