Wizards.one battles simulation
Recently new blockchain game Wizards.one had started for EOS-token holders on EOS mainnet. You already could buy & trade on marketplace for wizards/pets/accessories, and soon will be announced wizards battles possibilities.
Currently more then 25000 wizards already was generated and Wizards.one smart contract is keeping 9-10th places on Eos-Dapps with about 2400 weekly transactions for 290 EOS.
I've went through @wizards.one -> post with upcoming battles description. It is interesting ideas for attack mechanics. So, I've coded python script in order to simulate battles and estimate winning probability depends on wizards DNA properties.
Battle DNA generation
An unique DNA is generated with each wizard on EOS blockchain. It is used Normal distribution with mu = 50 and sigma = 8 for generation of 8 separate DNA genes. Each one DNA gene will control some one magic type ability.
MU = 50
SIGMA = 8
DNA = 8 # DNA nums
def generate_dna():
''' Generate Normal distribution '''
d_list = []
rnd = np.random.normal(MU, SIGMA, DNA)
# convert float to integer
for item in range(DNA):
d_list.append(int(round(rnd[item], 0)))
return d_list
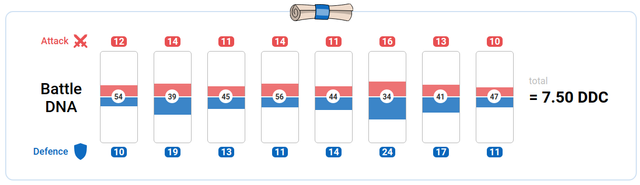
So, for example, for wizard #272 was generated DNA with 8 genes:
[54, 39, 45, 56, 44, 34, 41, 47]
DDC formula
The resulted distribution deviation will determine future success in battles. The more deviation, the better win probability. We could evaluate success as a higher mean deviation of DNA items distribution:
def bias(d_list, center):
''' Mean deviation '''
dna = np.array(d_list)
result = np.mean(np.abs(np.array(dna) - center))
return result
For the wizard #272, the DNA mean deviation is equal to 7.5. The game authors called this parameter as a DDC value.
Attack/Defence calculation
The DNA is used for calculation of attack and defence numbers with following algorithm:
for item in range(DNA):
delta = self.dna[item] - MU
if delta >= 0:
self.attack.append(SIGMA + delta)
self.resist.append(math.floor(SIGMA + (delta / 2)))
else:
self.attack.append(math.ceil(SIGMA - (delta / 2)))
self.resist.append(SIGMA - delta)
Wizard #272 has attack/defence values calculated from DNA accordingly:
Attack: [12, 14, 11, 14, 11, 16, 13, 10] Mean: 12.62
Resist: [10, 19, 13, 11, 14, 24, 17, 11] Mean: 14.88
You may notice that the attack/defence values are different in the wizards.one post and on the game web page for Wizard 272. I guess the numbers in the post are wrong. As I see, it is because of different rules of rounding float to integers. You should divide integer delta / 2 and get float result, then convert it again to integer. For example, be aware of function round() behavior in Python3:
In [1]: round(6.5)
Out[1]: 6 # Not 7
That is why actual mean of values of attack and defence may represent winning probability more precisely than DDC.
Win probability
I've ran simulations for 100K battles rounds to calculate how many times each wizard will win. And than repeat the test again several times in order to get win probability estimation.
The battle results between the wizard #272 (DDC=7.5) vs. random wizard (DDC=5.875):
$ ./wizbattle.py
Wizards.one battle simulator
Wizard '272' DNA: [54, 39, 45, 56, 44, 34, 41, 47] -> bias: 7.500
Attack: [12, 14, 11, 14, 11, 16, 13, 10] Mean: 12.62
Resist: [10, 19, 13, 11, 14, 24, 17, 11] Mean: 14.88
Wizard RAND DNA: [44, 50, 45, 48, 47, 42, 33, 56] -> bias: 5.875
Attack: [11, 8, 11, 9, 10, 12, 17, 14] Mean: 11.50
Resist: [14, 8, 13, 10, 11, 16, 25, 11] Mean: 13.50
Starting 100000 rounds...
TOTAL:
{"Wizard '272'": 50665, 'Wizard RAND': 32874, 'No winner': 16461}
Wizard '272' win rate: 60.6%
No win rate: 16.5
Mean ratio: 13.75 / 12.50 (1.10)
As you could see that attack+defence mean ratio between wizards was 13.75/12.50 = 1.10 or +10% for wizard #272 advantage. In comparison, the DDC ratio 7.5/5.875 = 1.27. The win rate for wizard #272 as well 60% (50+10). It means that in 60% of battles the wizard will be a winner.
So, the mean attack+defence ratio could be used for approximate win prediction. At the same time 16% of battles (or each 6 battles) will be drawn games and the winner will be selected totally random.
I wonder that so many random results exists in the battles. It is strange that wizards' accessories and pets are not influence to the battle results. So, what is the purpose to buy items in that case? Probably more expensive stuff will incentives opponents to battle and to have a chance to copy it. One more thing I would like have is to give names to owned wizards instead of to call it by ID numbers.
Update: In the most resent post wizards.one announced new alternative battles rules based on items properties. It looks more attractive!
Python simulator source code -> wizbattle.py.