¿La matemática es una ilusión o es real?
tenía tiempo sin hacer un post así, espero que te guste.
¿Descubierta o creada?
Si encontraramos vida extraterrestre, ¿cómo nos comunicariamos con ellos? La respuesta que la gran mayoría de cientificos te daría sería bastante directa: con matemática. Y es que la matemática siempre ha tenido ese estatus de lenguaje universal, no importa lo que digas, si no lo puedes comprobar matemáticamente no será más que una bonita historia. "No importa en que parte del universo estes, la matematica siempre se cumple", ¿cierto?
¿Qué pasa si te digo que esto es uno de los temas mas controversiales del mundo cientifico? ¿Es la matemática una realidad absoluta o una ilusión en nuestra mente?
Empecemos.
1+1=2
Todos conocemos la matemática, a algunos le gusta y otros la odian, pero no importa cual de los dos seas, todos estamos de acuerdo que es una de las más importantes bases de nuestra sociedad, todo nuestro mundo gira alrededor de ella. Y es que al ser tan increiblemente precisa describiendo el universo, es imposible no colocar a la matematica en un pedestal. Pero este mismo hecho es lo que hace que más de uno se pregunte, ¿cómo algo tan perfecto pudo haber sido creado por humanos? ¿es la matemática la regla que todo en el universo sigue o un lenguaje humano que nos ayuda a entender/describir lo que sucede a nuestro alrededor?
Esta es una pregunta muy difícil de contestar, o aunque sea de contestar correctamente.
Imagina que tienes una manzana en tu mano izquierda y otra en tu mano derecha, 2 en total. De la misma manera que las manzanas son frutas, son rojas y son dulces, ¿acaso su "2-sividad" es también una propiedad de las manzanas? Si sueltas una, ¿ya dejaron de ser 2? ¿o lo siguen siendo sólo que ahora están separadas? ¿es verdad que tenemos 2 manzanas o es sólo un concepto abstracto que existe unicamente en nuestro cerebro?

Descubriendo a la matemática
Primero supongamos que la matemática es una existencia real, no digo que respire y piense, más como un carro o una galleta. Pensando de está manera, estariamos diciendo que todos los conceptos matemáticos que conocemos son verdades absolutas del universo. Desde suma/resta y que el 2 le sigue al 1, hasta teorema de pitagoras y termodinamica. Todas estas son reglas del universo que los humanos descubrimos gracias a nuestros hermosos cerebros.
¡Esto suena bastante creible! Es la manera más simple de explicar la precisión con la que hemos llegado a describir muchas cosas del universo... Pero hay unos problemas con este tren de pensamiento.
Primero que nada, ¿a que nos referimos con que existe? Podemos tocar un carro o una galleta, pero... ¿alguna vez has tocado un número? ¿alguna vez has tocado una división? La respuesta que algunos dan, es que los números -y los conceptos matemáticos- son objetos abstractos que van más allá que el tiempo y el espacio. "Sólo porque no los veamos no significan que no están ahí". De la misma manera que decimos que existe crema entre 2 galletas de Oreo, existe un 2 entre un 1 y un 3. Esta "escuela de pensamiento" se conoce como platonismo, y como su nombre lo indica, su padre fue Platón. No todos los que piensan que la matemática es real piensan de la misma manera en la que él pensó, pero es un buen ejemplo de fallos en está manera de pensar.
Segundo, cada año avanzamos a grandes pasos en todo tipo de campos cientificos, y cada vez "descubrimos" nuevos conceptos y maneras de usar la matemática. Como estamos suponiendo que no la creamos, esto significa que -figurativamente hablando - hay una caja gigante llamada matemática en algún lugar del universo y que simplemente la estamos abriendo lentamente. En otras palabras, hay un ente que no conocemos, del cual no tenemos pruebas que existe, que rige la manera en que todo el universo funciona. HMMM, ¿donde he escuchado esto antes?
Tercero, podríamos voltear la tortilla y decir que la matemática es la versión real del universo, y que todo lo que vemos es la representación de una cantidad incontable de calculos que... ¿hace el universo? y que todo lo que vemos es la verdadera ilusión. ¿Pero cómo podriamos si quiera comprobar esto? Generalmente, cuando queremos comprobar un suceso en cualquier lado del universo, ya sea en el sól, un agujero negro, o en el patio de nuestra casa, usamos alguna ramificación de la matemática... ¿cómo podemos pobrar que la matemática es real usando más matemática?

Creando a la matemática
Ahora digamos que no descubrimos la matemática, supongamos ahora que la creamos. Si la creamos, podríamos pensar en la matemática como un lenguaje más, tal como el Español o el Ingles, pero mucho más preciso y universal.
Lo primero que se te puede venir a la mente es que los números (y los conceptos matemáticos) son simples maneras de describir el universo. En otras palabras, cuando dices
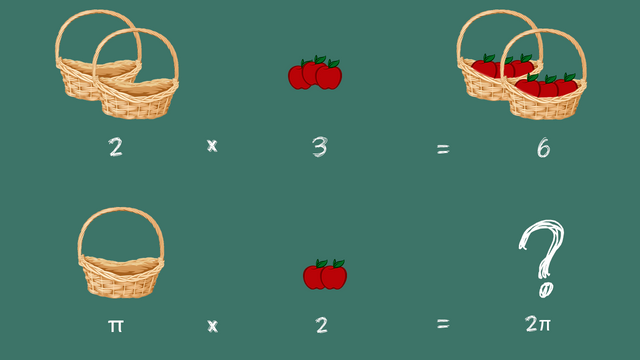
Eso simplemente representa que cuando tienes 2 canastas con 3 manzanas en cada una, tienes 6 manzanas en total. Y eso es todo, nada de pensamientos profundos ni filosoficos. Está suena muy convincente, es hasta practico.
"Si un leopardo corre a 58 km/h y quiere cubrir una distancia de 58 km, ¿cuanto tiempo tardaría?"
La respuesta es bastante obvia, pero la verdadera pregunta es está: ¿en que semestre le enseñaron física newtoniana a nuestro amigo, el Sr. Leopardo? Esto hace que nuestra teoría de que "la matemática es sólo una descripción" mucho mas creible. El leopardo no necesita saber matemática para correr, pero nosotros si necesitamos este lenguaje para transmirtir la información de su velocidad, de la misma manera en la que lo estoy haciendo contigo en este preciso momento.
Pero hay un problema. Si el número 2 representa una cantidad de canastas y el 6 representa la cantidad de manzanas, ¿qué cosa representa esta multiplicación?
Todos conocemos el número 2 y el número π (pi), el 2 puede significar dos manzanas pero, ¿es posible tener π canastas? ¿O √-1 canastas?... ¿Qué pasa cuando el numero no puede describir ningun objeto real? ¿Cómo un lenguaje que está "diseñado" para describir cosas, tiene "palabras" que no describen nada?
Imaginando a la matemática
Independientemente de que creas o no que lo relatado en la Biblia es veridico, todos estamos de acuerdo en que "amar al projimo" no es algo malo. La historia de El Señor De Los Anillos no está basada en hechos reales, hasta donde yo sé los hobbits viven en casas de tamaño normal, pero todos podemos aceptar que la camaradería y lucha por "el bien común" son valores muy bien apreciados en el mundo real.
Dentro del concepto de la historia, tiene sentido que Gandalf sea un mago, haya vivido por quien sabe cuanto, y que tenga una barba y una cabellera igual de poblada, ¿pero fuera de El Señor De Los Anillos? no mucho. ¿Esos conceptos matemáticos? No existen, son sólo una historia muy bien contada... O aunque sea esto es lo que dice el ficcionalismo matemático.
Por supuesto, esto también suena convincente en su propia manera, pero regresamos al comienzo de este post, ¿cómo los seres humanos hemos logrado crear un sistema -ya sea ficticio o no- que explica de manera tan exacta casí cualquier evento en el universo?
Es poco probable que podamos refutar la existencia de la matemática, más aún si planeamos hacerlo con más matematica, pero eso no es prueba de que exista o no. Puede que esto suene obvio pero, la unica matemática que conocemos y/o conoceremos, es matematica que bueno, es entendible por humanos.
Parafraseando: si un extraterreste nos intenta enseñar otro tipo de matemática, puede que ni siquiera sepamos de que habla. Así que la matemática que hemos descubierto/creado hasta ahora, es todo lo que tenemos, no hay una "matemática #2" que nos ayude a comprobar si "matemática #1" es real o no. Esto hace a la matemática una qualia de toda la humanidad.
Qualia: cualidades subjetivas de las experiencias individuales.

La habitación de Mary
En 1982, el filosofo Frank Jackson planteó el siguiente problema: Imagina una neurocientifica llamada Mary. Mary vive en una habitación blanco y negra, viste ropa blanca y negra, lee libros en blanco y negro, y su televisión solo muestra imagenes a blanco y negro. Mary, aún sin haber visto colores, es una experta en todo lo que tiene que ver con colores.
Fisica y biologicamente, desde longitudes de ondas hasta las celulas que son estimuladas por la luz en nuestros ojos, ella sabe absolutamente todo lo que puedes saber sobre el tema. Un día como cualquier otro, la tv muestra algo distinto, Mary ve por primera vez una manzana roja; por primera vez, ella puede experimentar algo que ella ya ha sabido durante años. Aquí la pregunta: ¿Acaso Mary aprendió algo nuevo?

Este problema cuestiona la diferencia entre saber y experiementar algo, entre lo fisico y lo teorico. Si el haber visto el color rojo por primera vez le enseñó algo nuevo a Mary, esto implica que hay estados mentales que no pueden ser descritos por completo. O en otras palabras, hay algo sobre ver colores que no puede ser sustituido por todo el conocimiento del mundo sobre los mismos.
Jackson no planteó este problema para explicarle a un ciego por que el rojo se siente "caliente" y por que el azul se siente "frio", esto es parte de una discusión que usa como metafora los colores para representar la consciencia humana, y el hecho de que puede, o no, haber sucesos que trascienden una representación fisica. Esto no es algo sencillo de responder, tendrías que pasar por lo mismo que Mary para tener una respuesta, pero es interesante, como minimo, imaginar en que manera afectaría nuestro problema de la matemática tanto si asumimos que el argumento del conocimiento (teoría detras de la habitación de Mary) es cierto o si su adversario, fisicalismo (argumento que dice que todo puede ser descrito fisicamente) tiene la razón.
Digamos que si hay sucesos que trascienden su representación fisica, cosas que no podemos describir con palabras o numeros, y ahora imaginemos un suceso cualquiera: una persona es rechazada por su enamorado o enamorada. Es posible representar la manera que se sentira nuestro protagonista ante el rechazo, ya sea las diferentes reacciones quimicas en su cerebro, su dificultad para respirar, las revoluciones por minuto de su ligera taquicardia y la velocidad con la que él desea salir corriendo. Todo esto es posible pero como lo dice el argumento del conocimiento, podemos describir todo eso pero aún existirá un algo que nos faltaría, tal le ocurrió a Mary con los colores... ¿eso significa que hay cosas que la matematica no puede describir? ¿que tan real haría eso a la matematica?
Peor aún, ahora supongamos que el fisicalismo tiene la razón, todo puede ser descrito con formulas fisicas y reacciones quimica. En un futuro, cuando nuestra tecnología llegue a ser capaz de clonar a un ser humano... ¿también podriamos clonar sus sentimientos y memorias con colocar números en una computadora?
... Si esto llega a ser posible, tendremos que prestar más atención al origen de la matemática, ¿descubierta o creada?

pd. me deja un mal sabor de boca terminar un post con la misma pregunta con que lo empece, pero si tuviera la respuesta estaría aceptando un Premio Nobel, no jugando league of legends hasta las 4am :p
Tiempo sin leerte, apenas leí tu post recordé la película "La llegada". Qué opinas sobre esa manera de comunicarse muy estilo de ficción o puede acercarse a la realidad... ;). Con los problemas que planteas recuerdo cuando Darwin mencionaba sus observaciones del comportamiento y las interrelaciones naturales para la selección natural. Fabuloso escrito compartes, me encantó la habitación de Mary. Saludos y feliz día.
Oh, no la he visto pero se ve súper interesante, por lo que me contaron toca mucho el tema de la comunicación... Hahaha siendo 100% honesto contigo, no tengo mucho conocimiento de las investigaciones de Darwin. Gracias! Te recomiendo este video si te gustó la habitación de Mary, es tremendo tema.
Saludos! :D
Esta es una discusión propia de la filosofía de la matemática. Si sirve de guía, yo concibo a las matemáticas como un sistema abstracto inventado y con cualidades de autonomía.
Es un "sistema" ya que son un conjunto de elementos relacionados.
Es "inventado" ya que es obra de una especie inteligente, en este caso, los seres humanos.
Es "abstracto" ya que existen en el plano de las ideas aunque sus propiedades pueden tener referentes en la experiencia física y en otros mundos abstractos, y
Tiene cualidad de "autonomía", ya que se independizan del hombre y crean nuevos objetos y sistemas que tienen que ser descubiertos. Es como si las matemáticas fuesen un ser vivo.
Buen post.
Debo admitir que no lo había pensado de una manera tan clara. Concuerdo en todo contigo, en especial en la autonomía que goza la matemática... Pero tengo curiosidad, ¿consideras a la matemática un sistema único o crees que el hombre pudo haber creado otro sistema igual de exacto y, por quien sabe cuantas coincidencias, tenemos la matemática que usamos hoy en día?
Eso me recordó un articulo que leí hace un tiempo sobre los agujeros blancos, algo que es matemáticamente posible pero que jamás ha sido visto
Saludos @eniolw, me alegra que te haya gustado :D
Buena pregunta. Este sería mi razonamiento para responder:
Por lo tanto:
Seres humanos diferentes e independientes entre ellos pueden identificar los mismos patrones e inventarse conceptos matemáticos similares para representarlos mentalmente.
Por ejemplo, la numeración decimal tomó como base los dedos de las manos. 10 dedos => 10 digitos (0,1,2,3,4,5,6,7,8,9 en números árabes). La aritmética, que es la más básica rama de las matemáticas, se inspira de las cosas que se hacen u observan en la cotidianidad. La necesidad de diferenciar cantidades de cosas, de marcar fechas, etc. son cosas que han obligado a inventarse conceptos para eso.
En mi opinión, la matemática es un lenguaje que con las leyes que la enriquecen revela "atajos" al descubrimiento de propiedades del mundo físico, aunque no siempre funciona.
Saludos!