Physics - Electromagnetism - Resonance in Series R-L-C circuits
Image contains: https://en.wikiversity.org/wiki/RLC_circuit
Introduction
Hello it'a me again @drifter1! Today we continue with the Electromagnetism series to talk about the Resonance of R-L-C circuits and more specifically Series R-L-C circuits. To not get lost you should read the previous articles about such circuits in the Mutual and Self Induction chapter, but also the previous articles of the current chapter! So without further do, let's get started!
Series R-L-C circuit
Let's start out with a small refreshment of the current knowledge that we have about R-L-C circuits. Such circuits are build up of three basic passive components of Resistance (R), Inductance (L) and Capacitance (C). When having a direct current (DC) only resistance is limiting the current flow, directly following Ohm's law. In such circuits or even AC circuits that have only resistance, current and voltage are exactly in-phase. When having an alternating current (AC) that follows a sinusoidal waveform, reactance comes into play, which is a property of capacitors (capacitive reactance) and inductors (inductive reactance) that opposes the change in current/voltage. This opposing effect of reactance causes a phase difference between the current and voltage. A capacitor stores the electric energy of the current flow inside of it's electric field to give it back later on (current is leading by 90 degrees), which means that a purely capacitive element doesn't dissipate energy. An inductor is affected by the effect of Electromagnetic Induction, which means that an opposing emf voltage is being induced in the pure (only inductance) inductor that causes the current to "lag" behind the voltage by 90 degrees. Combining the effect of both elements we find out that the voltage to current phase difference is in the range of [0, 90] degrees. The resistor (resistance) only limits the maximum magnitude of the current and is in-phase.
The voltage in such a mixed circuit can be described by so called voltage vectors that build up a so called voltage triangle. From this voltage triangle we get the expression for the total/sum voltage which is:
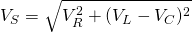
The same expression can also be found using Kirchhoff's voltage Law (KVL) and Mathematical Analysis calculations.
The combined effect of resistance R and reactance X is called impedance Z. Following a similar procedure to before using a so called Impedance Triangle or Mathematical analysis and Kirchhoff laws we get the following expression for the Impedance in a series R-L-C circuit:
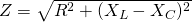
We can expand this expression even further by replacing the reactance of the capacitor and inductor with it's expression as following:
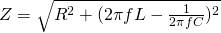
This expression shows us how the Impedance and individual Reactance's (XC and XL) are being affected by the frequency of the signal's oscillation. Another last thing that I might even forgotten to point out last time is that the phase angle θ is equal to the angle of the Impedance vector of the Impedance triangle, which means that the we also have the following trigonometric equations for that angle:
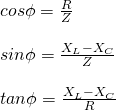
Of course more complex series rlc circuits that contain many resistors, inductors and capacitors can be reduced into such a simple circuit by including the total resistance R, total inductance L and total capacitance C, of each category alone. Knowing that there is no such thing as a pure inductor or capacitor and also no such thing as a pure resistor, all the elements have all three properties in "real life" applications.
Series Resonance
What's left now in today's topic is a more in-depth analysis of the so called resonance in such circuits. By that I mean that we now have to analyze the oscillation of current and voltage in a much deeper perspective, seeing where energy is being "gained", where it is being "lost" etc. As RLC circuits and more specifically the Reactance and Impedance of them are being affected by the Frequency we will get into the "frequency response" of such circuits. At a specific value/point that we call Resonant Frequency the circuits produce a so called Series Resonance . Of course only the reactance components of capacitance and inductors are affected...
Inductive Reactance and Frequency
Let's start out with the effect of frequency on inductors or more specifically the inductive reactance. As the Frequency or Inductance increases, the overall inductive reactance value also increases. Having the frequency approach infinity the inductor starts acting like an open circuit. Having the frequency approach zero, turning the circuit into a DC circuit. At this point the inductor acts like a short circuit. Inductive reactance is directly proportional (XL ∝ ƒ) to frequency and so small at low frequencies and high at higher frequencies.Capacitive Reactance and Frequency
In the same way, capacitive reactance is also being affected by frequency and capacitance, but in an opposite/reverse notion, compared to before. Capacitive reactance is inversely proportional (XC ∝ f^-1) to frequency and capacitance and so decreases as those two increase. As the frequency approaches infinity the capacitive reactance practically reduces to zero causing it to act like a perfect conductor. At zero frequency or DC level tthe capacitor's reactance reaches basically infinite level, causing it to act like a very large resistance. Such a big resistance turns the circuit into an open circuit, cause basically no current flows through the circuit anymore.Resonance Frequency
Until now we saw what happens for each element alone. Both of these Reactances depend upon the frequency of the supply. At higher frequencies the inductive reactance is higher then the capacitive reactance. At lower frequencies the capacitive reactance is higher then the inductive reactance. At a specific point that we call Resonance point the values of reactance for both components are equal. Graphing the curves of these two reactances with frequency, the resonance point is exactly at the point of intersection of these two curves.The graph below summarizes everything perfectly:
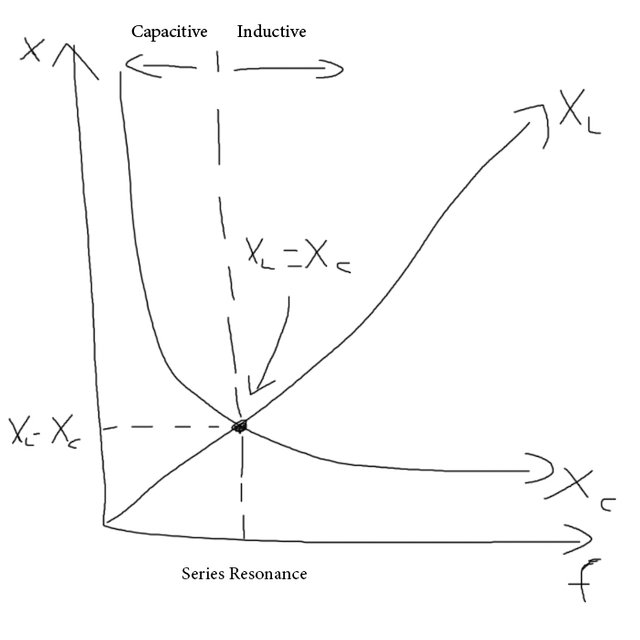
Based on graph at: https://www.electronics-tutorials.ws/accircuits/series-resonance.html
Yes, it's the same one that I had in the beginning. So what? :P
The resonance frequency can be calculated as:
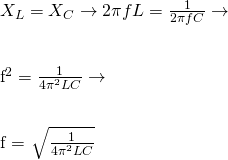
The final equation of Resonance frequency is therefore:
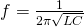
Series RLC circuit at Resonance
Let's now continue on, analyzing the Resonance even further!At the resonance point the two reactances of course cancel each other out, making a series LC combination acts as a short circuit. The only thing opposing the current in the circuit is therefore only the resistance R. In other words, the total impedance is now is only dependent on the resistance meaning that: Z = R. The impedance at resonance is called "dynamic impedance" and depends only upon the frequency. At higher or lower frequencies it will dominate either side (inductive or capacitive). The graph of Dynamic Impedance is:
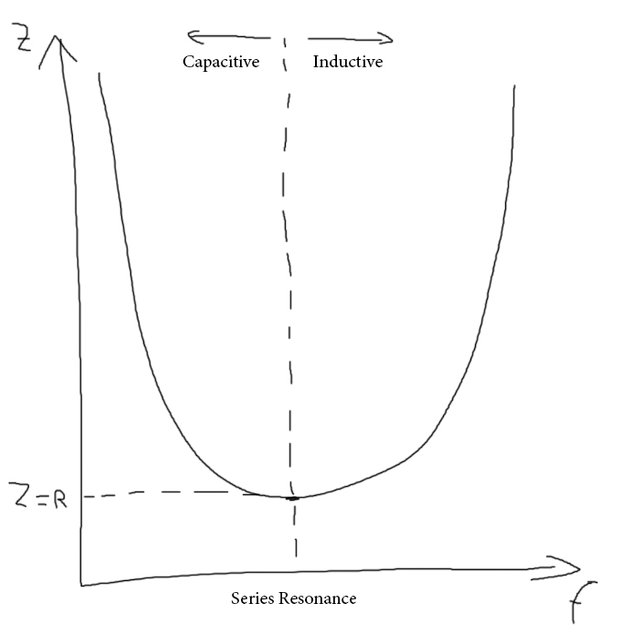
Based on graph at: https://www.electronics-tutorials.ws/accircuits/series-resonance.html
You can see how it follows a parabolic shape...
At series resonance VL = -VC, making the reactive voltages to be zero and so the supply voltage is dropped across the resistor (VR = Vsupply). Such circuits are therefore also known as voltage resonance circuits (parallel ones are known as current resonance circuits).
Being in a series resonance circuit we can also plot the magnitude of current as a function of frequency now. Doing that we see that the maximum value of current is at the exact point of resonance. At resonance frequency Imax = IR. At the other points or even at resonance the voltages across the inductor and capacitor can become many times larger then the supply voltage. At resonance these two voltages are equal and so cancel each other out, but on the other points everything starts to become more interesting...
The reactance components of capacitance and inductance have no effect at resonance and so current and voltage are now in-phase to each other. This can be proven easily using:
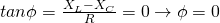
One last thing has to do with Selectivity and Quality that I will skip for today's post, cause you can read about it in the following link that explains it very well:
REFERENCES:
- https://www.electronics-tutorials.ws/accircuits/series-circuit.html
- https://www.electronics-tutorials.ws/accircuits/series-resonance.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/electric/serres.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous articles of the Electromagnetism series
Here we only have the previous two "chapters" and the current one....
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization
Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields
Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)
Maxwell's equations -> What they are, each equation analyzed separately
Electromagnetic Induction exercises -> examples all around Electromagnetic Induction
Mutual and Self Induction:
Mutual Inductance -> Mutual Inductance, applications
Self Induction -> Self Induction, Lenz's law, Inductance of a Coil
Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example
R-L circuits -> R-L circuit energizing, de-energizing, Characteristic time constant
L-C circuits -> L-C circuit, oscillations, energy cases, applications
R-L-C circuits -> R-L-C circuit, oscillation, applications
Mutual and Self Induction exercises -> examples all around Mutual and Self Induction
Alternating current:
Getting into Alternating current -> Phasor diagrams, Alternating current, Average (RMS) current and voltage, Differences, Advantages/Disadvantages
Electric Reactance in AC circuits -> Resistors, Inductor and Capacitor Reactance in AC circuits
Series R-L-C circuits Impedance -> Series R-L-C circuits, Phasor Diagrams, Impedance
Power in AC circuits -> DC Resistive circuit, Power in AC circuits (resistive, reactive), Power Factor
Final words | Next time
And this is actually it for today's post and I hope that you enjoyed it! Next time we will get into the Resonance of Parallel R-L-C circuits!
Keep on drifting!



Just as a small note. You can get the nice sinus in latex if you use the command \sin . The same holds for other trig-functions :)
Haha thanks! I will try it out next time :P
Nice post. It is not clear if your images have the right copyright for re-use. Could you add it? :)
Thanks! The images are from one of the references. I'm not exactly sure about the copyright policy on that science website...If there is a problem I can always replace them with self-made graphs, diagrams etc. Should I?
It would be advisable to do so, just to stay on the safe side! ;)
ok done ;)
Θενκς γιο'ρ οσομ!
I have a problem with the Digitizer's drivers in the new Windows 10 edition and so it's much more difficult to create such Diagrams, Graphs etc., but I hope that they came out well :)