Curved drawing lessons #2: The spherical geometry
Introduction
In lesson #1 we have shown that beyond a drawing lays a geometry which governs the different features represented in the image. This geometry bring us tools to measure distances, paths and angles as well as a way to compare one object among its neighbours through the perspective.
The most popular geometry is called Euclidean geometry learnt at every school since centuries. Euclidean geometry is then the most common mathematical support where graphics, paintings and illustrations are built. This geometry simply forwards visual information from the reference plane to the projected plane.
Since a plane has no curvature, drawings built over a plane are considered as flat drawings.
We have also enunciate the poor performance of this geometry. I summarize then here:
- small horizontal and vertical Field of View (around 50º).
- Objects outside Field of View are not represented in the projected plane or surface.
- Extremely low graphic density.
Finally, we have introduced a category called curved drawing which recalls to a different geometry.
In this lesson we will introduce a new kind of geometry, called spherical geometry which will help us to overcame the limits of Euclidean geometry.
The Earth is not a flat plane
Let's go back to our painter and observe what is in fact happening:
When I was at school, in my last year, I had an incredible mathematics teacher who was called Monsieur Aubry. Monsieur Aubry had enormous quotes which I have retain somewhere in my memory. Like this one:
Which in English means, you are unable to see beyond your own nose. Mathematics are nothing but the most pure and elegant art among all the arts. Mathematics requires to constantly think beyond limits and pray to have a happy idea to see things in a different way. But Monsieur Aubry also advise us not to talk about mathematics outside the classroom, so I will follow his advise and continue with my description.
Following Monsieur Aubry quote, let's zoom out from the scene of our old master painter, and let's see things in a different way:
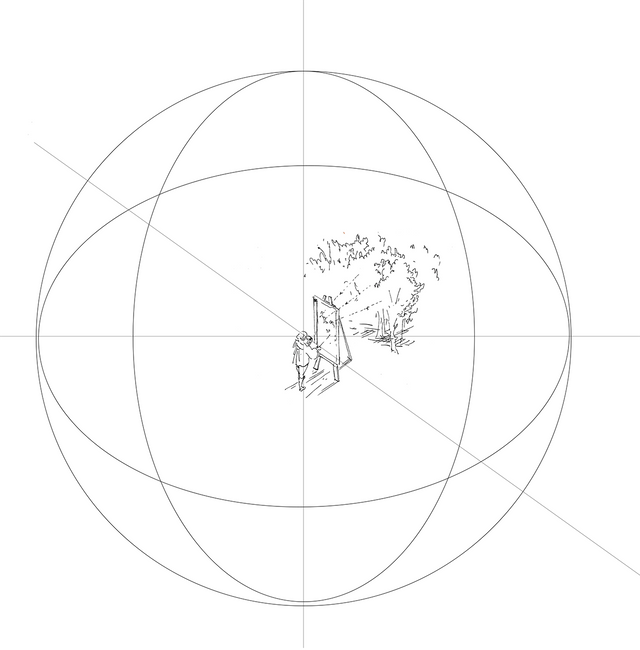 Vous êtes incapable de voir au de-là de votre propre nez -Monsieur Aubrey message to mediocre scholars- (Illustration from the author)
Vous êtes incapable de voir au de-là de votre propre nez -Monsieur Aubrey message to mediocre scholars- (Illustration from the author)In fact, we can assume that the world we see is projected into the surface of a sphere which center is located in the middle of our eyes (I am not considering here a stereoscopic model which would contain two spheres, one for each eye, just for simplify this subject).
Now, let's remove the flat canvas and bring to our old master painter a brush large enough to paint into the surface sphere:
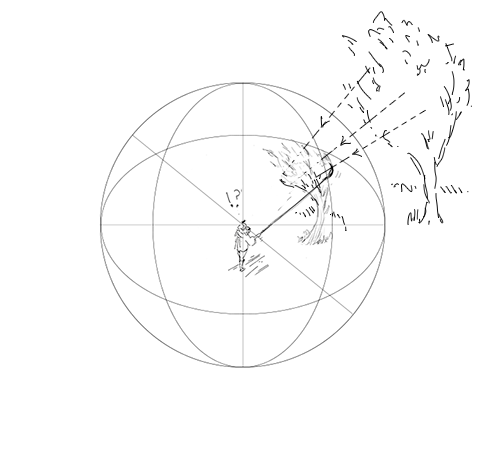
Old Master painter drawing into a sphere (Illustration from the author)
If this were possible, our friend painter could then draw on the entire surface of the sphere, not only in front of his nose, but in all directions!
I want to notice that every single dot in the world outside the sphere has a one and only intersection point in the surface of the sphere. Intuitively, close your eyes and imagine your head into a sphere, then trace a ray from the middle of your eyes to a spot in front of you. This ray will intersect somewhere with the surface of the sphere, but this intersection will be unique.
So with the sphere as the new projection surface we can:
- extend the FOV up to 360º Horizontal and 180º Vertical which is the FOV needed to make a panoramic drawing
- draw features located up, down, at the right, at the left, even we could draw our own nape!
We have good news, because this IS POSSIBLE. Let's see how.
Flattening the sphere: the Equirectangular projection
The sphere has unique properties among all the curved surfaces. Every point located in the surface of a sphere can be referenced by two angles. Those angles are the latitude and longitude:
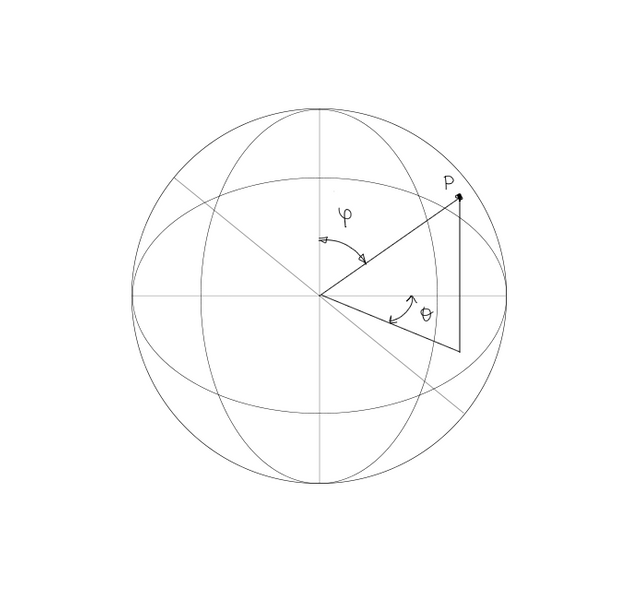 Latitude and longitude of point P located on the skin of a sphere(Illustration from author)
Latitude and longitude of point P located on the skin of a sphere(Illustration from author)I do not pretend, dear reader, to take you to your drawing location with a balloon in your head. There is a way to solve this problem and draw back into a flat support. Follow me!
For each point P located in the surface of the sphere we are going to register it's latitude and longitude in a flat plane:
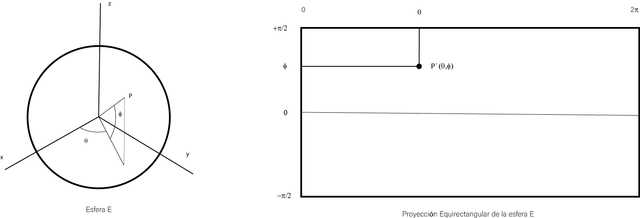
Equirectangular projection of a sphere (Illustration from the author)
So, in a sheet of paper, draw a rectangle which ratio is 2:1. In the horizontal axis we will refer the longitude of every point located in the sphere. In the same way, in the vertical axis we will transfer the latitude of the latter point. Since longitude is bounded in the interval [ 0, 360º ] and latitude in the interval [ -90º , +90º ] the length of the horizontal axis is double the length of the vertical axis.
This is going to be our new drawing support for the following lessons. It is a flat plane, in fact, but instead of locating points by its (x,y) coordinates, we located points by its (latitude,longitude) angles.
As you are curious to see how a drawing looks like in this new support, here are some examples:

Marché des Halles, Angoulême, France, freehand 360º drawing, March 2018 (Illustration from the author)

Now, it is very important to outline how this spherical geometry transforms the information:
- Straight lines are no longer straight lines but geodesics lines
- Angle are no longer maintained. The sum of three angles of a triangle is no longer 180º like all our school mathematician teachers told us.
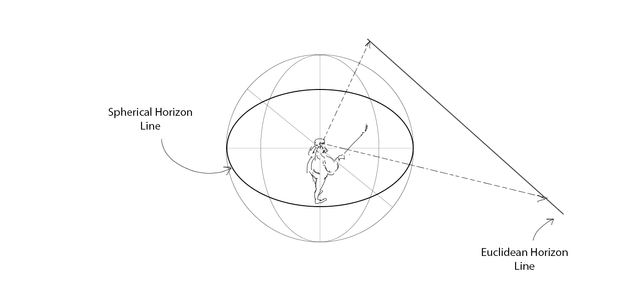
And, finally, maybe some of you are wondering what happens with the horizon line, which was an infinite straight line in our Euclidean geometry:
Well, the horizon line is no longer an infinite straight line but a circle, Monsieur Aubry would have call this a maximum circle.
Ok, your mind is blowing now, I will stop this lesson here. Just for your information, in the modern an western world it has been agreed that a practical demonstration of the sphericity of the Earth was carried out by the sailors Ferdinand Magellan and Juan Sebastian Elcano on his circumnavigation expedition of the world (1519-1523) (source wikipedia).
Meanwhile, graphic illustrators, painters, sketchers, has been thinking for more than 25 centuries that the horizon line was an infinite straight line. A mathematical update was then necessary. So, ladies and gentleman it is time to send to Mr Euclides to retreat, with honor.
Summary
In this important lesson we have describe the spherical geometry which is based in the sphere. With this geometry the constraints found with Euclidean geometry has been relaxed. So, now it is possible to:
- draw images with a Field of View up to 360º vertical and 180º Horizontal
- draw features located up, down, at our right, left or back.
- boost the graphic density, as in the same sheet of paper we can represent a spherical universe.
Also, this geometry transforms straight lines into geodesics and does not maintain angles.
We have also describe a way to flatten the sphere into a flat support in order to avoid going drawing with a beach ballon in our head, the equirectangular projection. The next lesson will be focused on how we can freehand draw onto this new support and how we can achieve a 360º drawing.
It has been a deep an intense class, but, this lesson is crucial to understand the foundations of spherical drawing.
Again, thank you for reading and stay tune to this course!
Have fun!



i love these lessons, @javier.dejuan !!! very well written, and very, very WELL illustrated <3 wonderful post !!!
upvotes, curates, and resteems
thank you very much, my friend @veryspider! I ll keep pedaling!!
Hi javier.dejuan,
Visit curiesteem.com or join the Curie Discord community to learn more.
thank you very much @curie team.
this is definitely exciting!
Great work! Need to try this.
Thank you for sharing :)
Congratulations @javier.dejuan! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - The results, the winners and the prizes
Arrechisimo!!!
Congratulations @javier.dejuan! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - The results, the winners and the prizes
A really great post, Javier. It is both beautiful and informative. I shall feast my eyes upon it ^_^.
-upvoted-
oh! thank you very much @scrawly, more to came in the next days!
This post was shared in the Curation Collective Discord community for curators, and upvoted and resteemed by the @c-squared community account after manual review.
wow, pretty cool explanation and completed. ^^
i will save it, it will be very helpful for future design and paints :D
thanks friend, for all this information and help
If I get to convert an artist into a "spherical" artist, it would have been worth it
Or maybe a mix between spherical art and other techniques :D
it is always good to learn from the best ones, but also to test different things from them :)