Requirements:
BFS
DFS

Uniform Cost Search is the best algorithm for a search problem, which does not involve the use of heuristic function. UCS finds the optimal path between the two nodes in directed or undirected graph. When all step costs are equal, breadth-first search is optimal because it always expands the shallowest unexpanded node. By a simple extension, we can find an algorithm that is optimal with any step-cost function. Instead of expanding the shallowest node, uniform-cost search expands the node n with the lowest path cost g(n). This is done by storing the frontier as a priority queue ordered by g(n).

Heuristic function is estimated cost of the cheapest path from the 
state at node n to a goal state which is known at the beginning.
Heuristic function are only given for a search algorithms which 
come under informed search while UCS is uninformed search.

Frontier is the set of all leaf nodes available for expansion at a
given point here which is stored as a priority queue with highest 
priority for node with smallest cost path. 

ref:: Artificial Intelligence: A Modern Approach 
       by S.Russell and P.Norvig

Uses/Application of UCS:
Imagine You have map of state with distance mentioned between all adjacent cities now you want to travel from city 1 to city 8 but you have several different combination of routes to select. In such cases UCS can be used to select an optimal path. By considering cities as individual nodes and distance as cost of traversal between two nodes.

Lets take the directed graph given below as example:

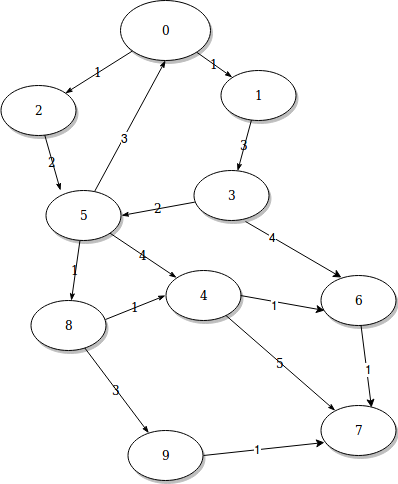
These are all the possible paths to reach from node 0 to node 7 with the cost of traversal
path: 0->1->3->5->4->6->7 cost: 12
path: 0->2->5->4->6->7 cost: 9
path: 0->2->5->8->4->7 cost: 10
path: 0->1->3->5->8->9->7 cost: 11
path: 0->2->5->8->9->7 cost: 8
path: 0->1->3->5->4->7 cost: 15
path: 0->1->3->6->7 cost: 9
path: 0->2->5->4->7 cost: 12
path: 0->1->3->5->8->4->7 cost: 13
path: 0->2->5->8->4->6->7 cost: 7
path: 0->1->3->5->8->4->6->7 cost: 10

best path: 0->2->5->8->4->6->7

Python Code:

import copy
import Queue as Q

class Graph:

# graph dictonary contains all the adjacent nodes of each as key and value pair
# cost_dict contains cost of each edge traversal of (u,v)
# final_dict contains all the possible paths from start node s to goal node g with total cost
def __init__(self):
    self.graph = dict()
    self.cost_dict=dict()
    self.final_dict=dict()

# u and v are nodes: edge u-->v with cost c 
def addEdge(self,u,v,c):
    
    if u not in self.graph:
        qu = Q.PriorityQueue()
        self.graph.update({u:qu})

    self.graph[u].put(v)
    self.cost_dict.update({(u,v):c})
    
# Makes a list to keep track of visited nodes
def tnode(self,n):
    self.visited = [False]*n


def UCS_util(self,s,visited,path,goal,value):
    # Appending node to the current path 
    path.append(s)
    # Marking that node is visited 
    visited[s]=True
    
    # If goal node is reached save the path and return
    if goal==s:
        self.final_dict.update({tuple(path):value})
        return
    
    # Checking if the adjacent node is been visited and explore the new path if haven't
    for i in self.graph[s].queue:
        if visited[i]==False:
            # When new path is being explored add the cost of that path to cost of entire course traversal
            # Send a copy of path list to avoid sending it by reference
            self.UCS_util(i,copy.deepcopy(visited),copy.deepcopy(path),goal,value + self.cost_dict[s,i])

def UCS(self, s,goal):
    self.visited[s] = True
    # List to hold all the nodes visited in path from start node to goal node 
    path=[s]
    
    for i in self.graph[s].queue:
        if self.visited[i] == False:
            # Make a variable to hold the cost of traversal
            value = self.cost_dict[s,i]
            self.UCS_util(i,copy.deepcopy(self.visited),copy.deepcopy(path),goal,value)

# Display all the paths that is been discovered from start node to Goal node
def all_paths(self):
    # Check if there is any path
    if bool(self.final_dict):
        print("All the paths: ")
        for i in self.final_dict:
            print "path: ",i,"cost: ",self.final_dict[i]
    else:
        print "No Path exist between start and goal node"

# Find the most optimal path between start node to goal node
def optimal_path(self):
    if bool(self.final_dict):
        print "best path: ",min(self.final_dict, key=self.final_dict.get)
    else:
        print "No Path exist between start and goal node"

Creating Graph object and assigning number of nodes

g = Graph()
g.tnode(10)

Making the Graph

g.addEdge(0, 1, 1); g.addEdge(0, 2, 1); g.addEdge(1, 3, 3);
g.addEdge(2, 5, 2); g.addEdge(3, 6, 4); g.addEdge(3, 5, 2);
g.addEdge(4, 6, 1); g.addEdge(4, 7, 5); g.addEdge(5, 4, 4);
g.addEdge(6, 7, 1); g.addEdge(5, 0, 3); g.addEdge(5, 8, 1);
g.addEdge(8, 4, 1); g.addEdge(8, 9, 3); g.addEdge(9, 7, 1);

0 is start node and 7 is goal node

g.UCS(0,7)

Find all the path between 0 and 7

g.all_paths()

Find the most optimal path between 0 and 7

g.optimal_path()

Output:

All the paths:
path: (0, 1, 3, 5, 4, 6, 7) cost: 12
path: (0, 2, 5, 4, 6, 7) cost: 9
path: (0, 2, 5, 8, 4, 7) cost: 10
path: (0, 1, 3, 5, 8, 9, 7) cost: 11
path: (0, 2, 5, 8, 9, 7) cost: 8
path: (0, 1, 3, 5, 4, 7) cost: 15
path: (0, 1, 3, 6, 7) cost: 9
path: (0, 2, 5, 4, 7) cost: 12
path: (0, 1, 3, 5, 8, 4, 7) cost: 13
path: (0, 2, 5, 8, 4, 6, 7) cost: 7
path: (0, 1, 3, 5, 8, 4, 6, 7) cost: 10


best path: (0, 2, 5, 8, 4, 6, 7)