About LPSolve

Simply, LPSolve is a mixed integer linear programming (MILP) solver. In order to understand this, you need to know the concept of linear programming first. Linear programming (LP), by definition, is a method used to obtain the best strategy while satisfying the specified requirements where both the objective function and the constraints are expressed as linear relationships.

For a two-dimensional LP, you can easily solve it graphically. For a three-dimensional LP, since its feasible region is composed by a three-dimensional space, few people are able to solve it graphically. For even higher dimensional LP, it is impossible to solve it graphically. Fortunately, we have an open source solver LPSolve to solve those LPs for us automatically.

The github repository of LPSolve is available at:
https://github.com/datumbox/lpsolve.

LpSolve Java wrapper was originally developed by Juergen Ebert, and the latest version of LPSolve is available at:
https://sourceforge.net/projects/lpsolve/files/lpsolve/.

How to install LPSolve

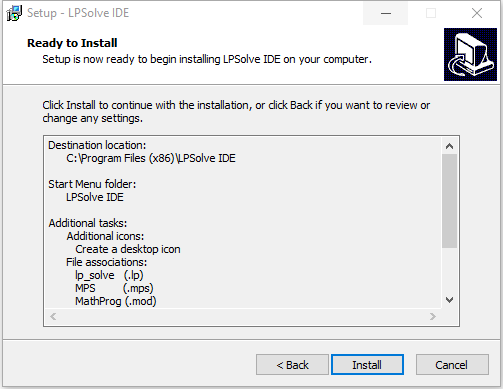
The installation process is quite straightforward. As most of the soft wares, you can specify the installation location. Additionally, it allows you to customize file associations. After installation, you are ready to go.

The operating environment of LPSolve is shown in the following image.

How to use LPSolve

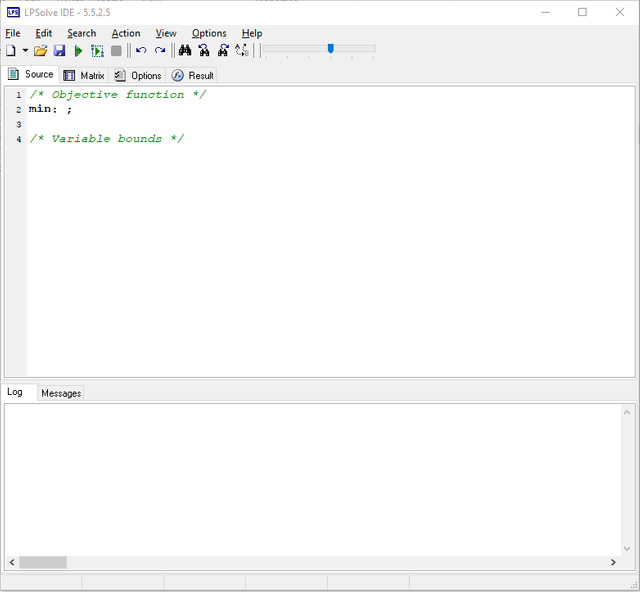
Standard format

The standard format for modeling an LP with LPSolve is quite simple:

• The objective function starts with “max:” (maximization problems) or “min:” (minimization problems), followed by a linear relationship which represents the goal of an LP, and ends with a semicolon (;);
• The constraint is formatted as a linear relationship ( >, <, >=, <=, =) followed by a semicolon (;);
• You can add a comment by starting a sentence with an asterisk (*) in that row.

Note that LPSolve does not show superscript and subscript as shown in the mathematical equations.

Solving an LP problem

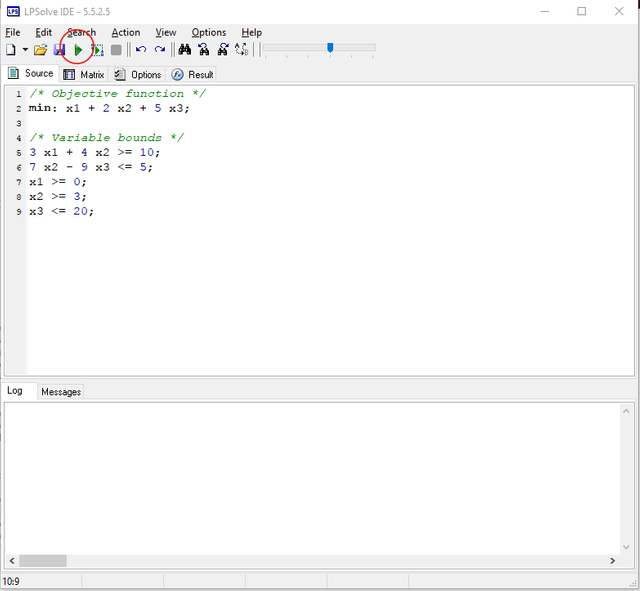
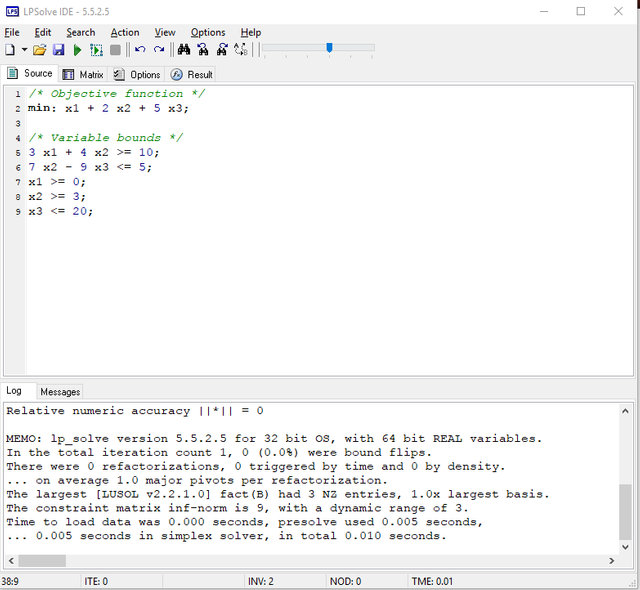
Let’s look at an LP model:

To minimize:
z = x₁ + 2x₂ + 5x₃
Subject to:
3x₁ + 4x₂ >= 10
7x₂ – 9x₃ <= 5
X₁ >= 0
X₂ >= 3
X₃ <= 20

The LPSolve format of this LP problem is shown in the following image.

When you finish typing both the objective function and constraints, you can simply solve it by click the green triangle as shown in the image above.

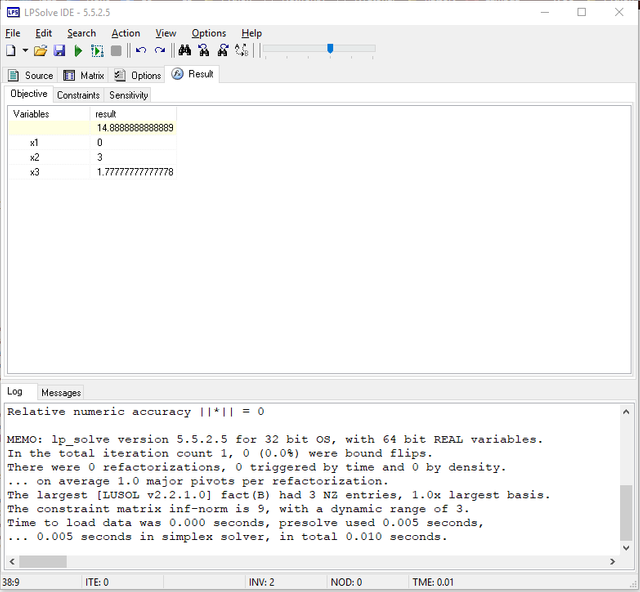
Because this is a very simple LP, you can get the result almost instantly, as shown in the image below.

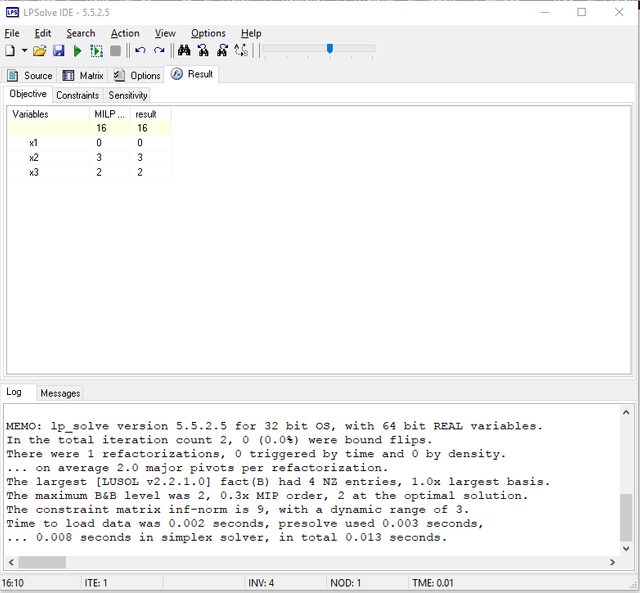
The bottom section of LPSolve shows the log. As can be seen, it took 0.01 seconds to solve this problem.

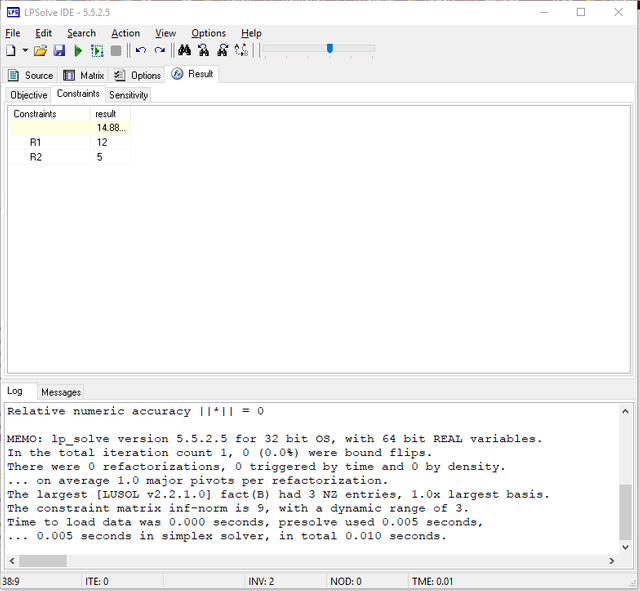
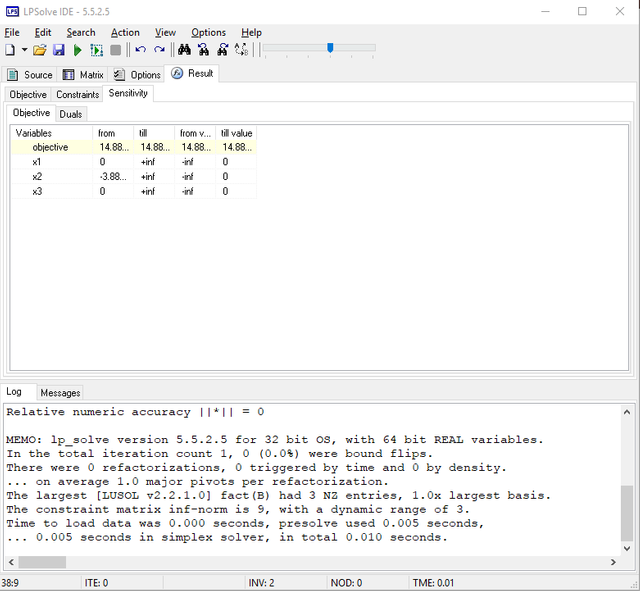
As can be seen, there is a tab called “Result” right above the working area. Clicking it, you are able to see three tabs: objective, constraints, and sensitivity. The objective tab shows the value of objective function and all the variables.

Solving an MILP problem

The variables in the above LP are all continuous. When at least one of the variables is an integer, the LP is referred to as MILP. Next, let’s modify the above problem a little bit by letting the variables to be integer. This can be done by simply use the keyword “int”, as shown in the following image.

By clicking the green triangle again, the new problem is solved. The result is illustrated in the following image.

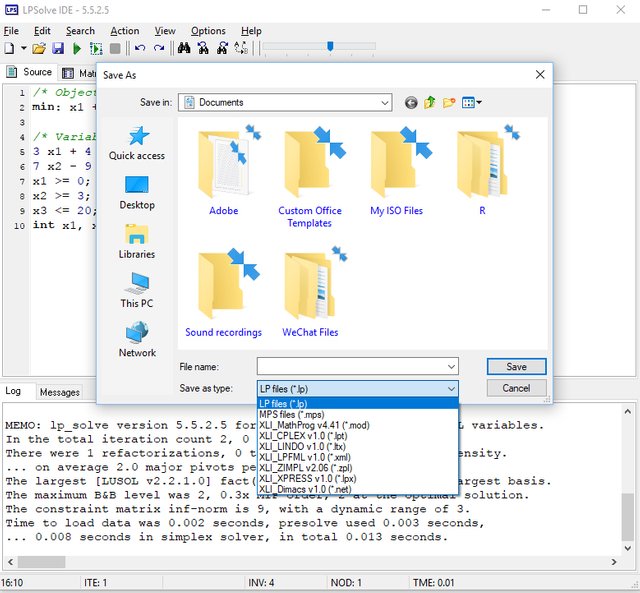
Once you get the result, you can save it as different formats as required. The formats supported by LPSolve are shown in the image below.