Non-lineair rewards: convergent linear vs fish-size bonus
At this moment STEEM has linear rewards. Currently Steemit INC is communicating its support for an Economic Improvement Proposal by @trafalgar, and there is talk of moving from linear to convergent linear rewards .
In a blog by @vandeberg, it is made clear what type of curve Steemit Inc is looking at for implementing this proposal.
Many people reading Steemit Inc's blog or the one by @vandeberg will get lost in the way the rewards are explained. In this post I want to try and explain how the proposed convergent linear proposal would differ from the current linear model. In the current model a vest is a vest or one point of steem power is one point of steem power no matter how many vests or steem power you have (1 SP is approximately 2000 vest). So if we look at the value of every little bit your vesting power as function of how many of these little bits you own, this value, with respect to the rewards system can be expressed simply as:

Now in the proposals that Steemit Inc has gaven its public support for, it seems Steemit Inc wants to replace this fair and simple but arguably somewhat problematic function by the following:
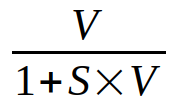
What is important to understand about this formula is that we have some kind of scaling constant S, and for smaller values of V (our vesting shares), this formula is dominated by the 1 below the division line, while at higher values of V the part above and the part below the division converge to being almost equal so the result of the equation converges towards one. This sounds sorta like a reasonable curve to solve the problem of larger stake holders setting up armies of puppet accounts and breaking the system in all sorts of patterns of bad behavior. But there is a problem with the math, a serious problem with the math. The problem is, this curve is in no way a scaling curve. Dimension the curve to incentify dolphins not to break up their stake into hundreds of redfish account and you will have near to nothing to incentify orca's not to break up their stake into hundreds of minnow accounts, let alone whales. Dimension the curve to incentify orca's not to break up their stake into hundreds of minnow accounts, and you will screw over redfish accounts so badly that the incentive for new users to join the platform should become close to zero.
So what are the alternatives? Can we devise a scaling curve or other reward scaling function that actually scales and is fair in that in incentivies dolphins, orcas and whales alike without totally screwing over new users?
My proposal proposes to start of with the following scaling curve:
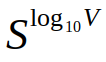
This curve would result an incentive that scales equally for each fish size and doesn't hit new account as hard as any of the envisioned curves for the convergent linear reward. The scaling factor S here is a bit different than the one in the previous equation. In this equation S is a scaling factor slightly higher than one (for example 1.01, 1.025 or 1.05).
Remember, in the STEEM ecosystem the concept of fish-size has meaning to the community. What the above formula tells us that for an S of 1.01, someone with ten times the stake (or one fish size higher) will get a 1% bonus added to the effective value of his stake. As fish sizes align on vest at powers of ten, we can make the above more in line with how users experience the platform, while at the same time incentify users to buy more SP and power up further to the next fish size level.
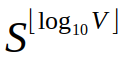
By adding the floor function to our curve, our reward scaling curve stops being a smooth curve, and instead gets properties that should be easyer to explain to the comunity. We keep the scaling property of the previous curve, but we also add a bit of user experience improvement. The above reward scaling formula for an S of 1.01 simply translates to a one percent fish-size bonus for every fish-size transition.
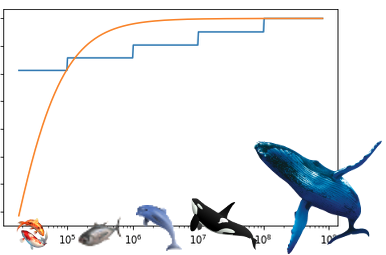
In the below graph we see a scaling function for a convergent lineair reward (orange) compared to a scaling function for a fish-size bonus (blue). I've put in the different fish sizes to illustrate the difference in a way I hope everyone can grasp.

I hope that in this blog I have shown the flaws of the convergent linear approach for the reward curve and have shown that a fish-size bonus reward scaling function could be fair, simple and scalable across all fish sizes while at the same time create extra insentive for users approaching the next fish size to buy some extra STEEM and power up.
If I understand your formula (and the blue line that represents it) correctly then this will fail horribly with the first sibil attack.
What stops someone from creating many empty accounts and vote with them? They have a scale of 1 which would give them some influence over the reward pool with zero stake. That is not sustainable.
Unless I understand your proposal wrong, in which case please elaborate and compare your proposed curve with the existing curves in a graphical way :)
The curves are scaling curves. That is, it is a curve representing the effective per vest value of account stake. The current linear reward curve as scaling curve would simply be a straight horizontal line slightly below the convergence of the blue and the orange lines in this representation.
If you would take your 500+ MV and split it up into 1000+ 0.5 MV accounts, those three orders of magnitude for the blue line would result in a decrease in effective value to S^-3 times the current effective value. So if S is set to 1.025 for example, the total effective value of your vesting shares would be reduced to 92.86% of your current value.
If you did the same with the current linear reward, the total effective value of your vesting shares would remain at 100.0% of your current value.
With the proposed convergent linear reward (the orange line) that Steemit Inc is currently speaking out its support for, you can pick a value for S (different type of S) to fit a desired incentive level between two set account sizes, but the problem is doing so doesn't create the same incentive at a wider range of account sizes.
If you look at the orange line, tuned for Orca incentive to make my point, Orca accounts are effectively yet modestly incentified not to break up their account into 100 or more smaller accounts. But looking at whales, there is little to zero incentive for a whale not to break up his stake into 100 or more smaller accounts, so no scaling up. Looking at a dolphin account, the incentive for a dolphin not to break up his stake into a hundred or more accounts is over the top and as a result, new accounts are hit really hard by this curve that is tuned for Orca incentive. This I hope shows the orange line is unfair and lacks scaling.
In contrast, the blue line creates equal incentives for dolphins, Orcas and whales not to break up their stake into 100+ puppet accounts.
Hope this clarifies the curves.
Can you plot your scaling curve on the mvest scale? Basically have x be MVEST and y be $ vote value?
I think that is in the end the metric we all can grasp. And any discussion about it needs to show how it differs in this comparison from other curves and why that is good.
Edit: your current plot compares apples with oranges, as the other curves all apply on the resulting rshares and your curve applies per voter. Which makes a difference, as your x axis is personal vests in your blue line but rshares on the post in the orange line.
No oranges, all apples! Comparing reward scaling functions to reward scaling functions, that is what my blog post is about. Maybe read @trafalgar's post for some background on the orange line. @trafalgar talks in terms of n^2/(1+n) that as scaling function translate to n/(1+cn)
In this plot the X axis is in VEST on a log scale (added the fish type graphics to make it understandable to people who don't think in terms of MVEST)and the Y axis represents . The Y axis can ve seen as $ vote value "per MVEST".
You could multiply each of the equation by some c x V, but doing so will just show slightly curved almost linear lines that truly don't communicate what the "per MVEST" graph communicates. That's the whole problem I am trying to address here. If you use a lineair X axis or plot $ against MVEST or both, you end up obfiscating that whatever S you choose for the orange curve, you either allow orcas and whales to not be incentified to good behaviour, or you end up screwing over new accounts so badly that you basically end up stating that we are full and new accounts are no longer welcome.
But in case you want to play with the scaling equations a bit, here is the code I used to make this graph:
Hope this one helps. Removed the floor function as that one seems to truly confuse you while its sole purpose was to take away confusion for the average user, so if it confuses you it loses its purpose.
The blue line is the current linear reward n -> c.
The brown, pink and gray line are the linear convergent rewards Sn/(1+Sn) -> c/(1+Sn) for different values of S.
The orange, green and purple lines are my nS^log(n)-> S^log(n+c) lines for different values of S.
Again, note that the scale for X is logaritmic, while the Y axis is linear and conveys the reward per unit of influence in order to clearly demonstrate the scaling properties of the reward scaling functions.
Agreed. The big issue with the convergent linear proposal is that it penalises low earning posts heavily to prevent a single entity spreading their stake over many small accounts. However it cannot differentiate between such accounts and actual small accounts. Since 70-75% of accounts earn less than 1 Steem per month, this is a pretty big issue.
For me the cons of the convergent linear are that:
(a) It reduces earnings for new / small accounts, thus harming mass adoption.
(b) It harms engagement by reducing the incentive to make comments, which typically gain low rewards.
Whilst your solution is elegant, it still pushes rewards away from low earners towards higher earners, although to a much smaller extent than convergent linear.
I think the proposal in the EIP to move away from linear is unnecessary. The original issue being raised, that of a large account splitting into smaller accounts, could be tackled through other avenues, such as using data analysis through MIRA to bring such accounts to light.
If I had seen this a week ago, I'd have pushed it to the top of the comments. We all need to listen to miniature -tiger.