Python Playground #1 - Plot Math like a pro
This is a new series of tutorials, in which there will be exercises with real problems and solve using Python language.
Although the language has completed more than 25 years but gained its popularity through Data Science, Artificial Intelligence in recent years.
Currently, tech companies are hiring Python developers in large number. They know the potential of this language i.e. programming-friendly due to its high-level language property.
Software tools
We will be using Jupyter Notebook in Anaconda package manager. Click here for installation guide.
Libraries (used here)
numpy, matplotlib, scipy
Coding
Diffferential
Here, we have to find the comparison b/w numerical derivative and analytical derivative.
Numerical derivative
The mathematical formula is as follows:-
Now, in python code:
# Numerical derivative
def forward_diff(y, x):
"""The function computes the forward differentiation"""
deriv = numpy.empty(y.size-1)
for i in range(deriv.size):
deriv[i] = (y[i+1] - y[i])/(x[i+1] - x[i])
return deriv
deriv = forward_diff(y, x)
Analytical derivative
The mathematical formula is as follows:-
The python code for this: -
deriv_exact = y * numpy.cos(x) # analytical derivative
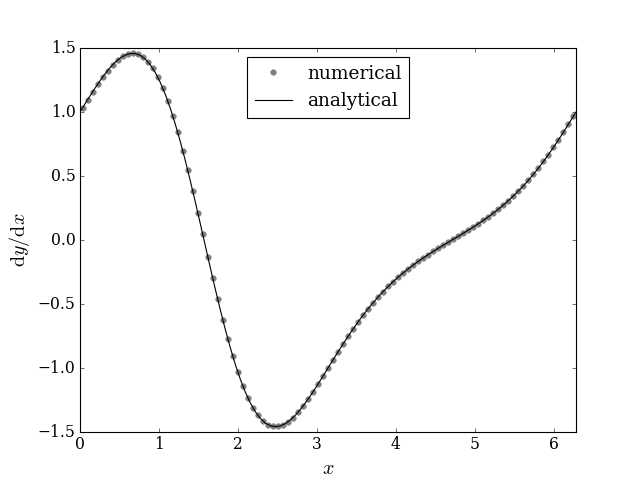
Code for Plots comparison
The complete code for comparison of the plots is as follows:
import numpy
from matplotlib import pyplot
%matplotlib notebook
x = numpy.linspace(0.0, 2 * numpy.pi, 100) # x variable
y = numpy.exp(numpy.sin(x)) # y variable
#numerical derivative
"""The function computes the forward differentiation"""
def forward_diff(y, x):
deriv = numpy.empty(y.size-1)
for i in range(deriv.size):
deriv[i] = (y[i+1] - y[i])/(x[i+1] - x[i])
return deriv
deriv = forward_diff(y, x)
#analytical derivative
deriv_exact = y * numpy.cos(x)
#plot the required derivatives
pyplot.figure() # displays the figure
#plot of numerical derivative
pyplot.plot((x[1:] + x[:-1])/2.0, deriv,
linestyle='None', color='gray', marker='.', label='numerical')
#plot of analytical derivative
pyplot.plot(x, deriv_exact,
linestyle='-', color='k', label='analytical')
pyplot.xlabel('$x$')
pyplot.ylabel('$\mathrm{d}y/\mathrm{d}x$')
pyplot.xlim(0.0, 2 * numpy.pi)
pyplot.legend(loc='upper center', numpoints=1) # numpoints define the no. of dots and length of line
Computation time diff
Whenever building the custom function, it's always better to check if there is an existing function for this.
So, we should compute the time of respective functions - Which is faster?
Now, let's calculate the computing time for numerical derivative by numpy library and deriv (defined above):
The python code for this:
#comparison in computing time
%timeit numpy_deriv = numpy.diff(y)/numpy.diff(x)
%timeit deriv = forward_diff(y, x)
#check whether the code result close?
numpy_deriv = numpy.diff(y)/numpy.diff(x)
print('Are they close? {}'.format(numpy.allclose(numpy_deriv, deriv)))
Integral
The x and y values used above are same in this case:
Numerical Integral
integral_numerical = 2 * numpy.pi * y[:-1].mean() # or 2 * numpy.pi * numpy.mean(y[:-1])
Analytical Integral
Here, we use the Bessel functions for calculating analytical integral:
Comparison
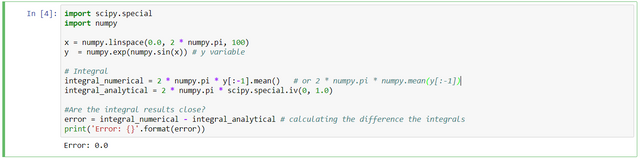
The python code for this is as follows:-
import scipy.special
import numpy
# Integral
integral_numerical = 2 * numpy.pi * y[:-1].mean() # or 2 * numpy.pi * numpy.mean(y[:-1])
integral_analytical = 2 * numpy.pi * scipy.special.iv(0, 1.0)
#Are the integral results close?
error = integral_numerical - integral_analytical # calculating the difference the integrals
print('Error: {}'.format(error))
So, there is no difference between the numerical and analytical integrals.
That's all.
Thanks for going through this tutorial.
Stay tuned for more such tutorials in this series.....
Follow series in Github
View in Steemit
Posted on Utopian.io - Rewarding Open Source Contributors

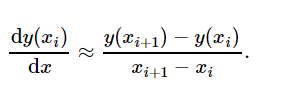
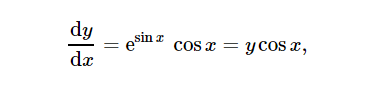

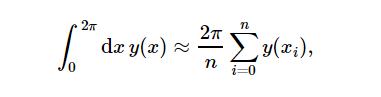
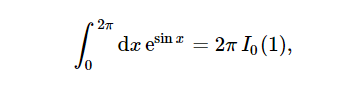
Can you please remove the Gifs? Your post has been approved, but Gifs saying UpVote, Follow and Resteem are not allowed on the post.
Thank you for the contribution. It has been approved.
[utopian-moderator]
nice post, i have resteem for you for free
Resteem by @jossylink
Resteem your post at SBD 0.001
Hey @abhi3700 I am @utopian-io. I have just upvoted you at 3% Power!
Achievements
Suggestions
Community-Driven Witness!
I am the first and only Steem Community-Driven Witness. Vote for my Witness. Lets GROW TOGETHER!
Up-vote this comment to grow my power and help Open Source contributions like this one. Want to chat? Join me on Discord https://discord.gg/Pc8HG9x
Great post.
Follow me and Send SBD 0.001 with your url as memo for Resteem by @jossylink
Oh