Tauchain Advanced Concepts
Tauchain Advanced Concepts
This is an introduction to some of the more advanced concepts in Tauchain. Concepts which make up the foundation of Tauchain such as computational trinitarianism which includes propositions as types, programs as proofs, and the relation between type theory and category theory.
Propositions as Types
Most programmers have an idea of what types are. For example in C/C++ you have types such as int (integer) char (character) bool (true/false) and float (floating point). Through the use of types in C++ a person can do something basic such as:
#include <iostream>
using namespace std;
int main()
{
int a, b;
cin >> a >> b;
cout << a + b << endl;
}
In this rudimentary example we have a C++ program which adds by taking input using cin, to pass to variables a and b, and then a very simple a+b adds them together. The important point here is that the int is the type for integer.
Programming languages have type systems. The C++ type system was used because C++ is a very familiar language but all languages have type systems. The mathematics behind the type system is called a type theory and in particular Tauchain uses a very unique state of the art type theory called intuitionist type theory. An alternative to intuitionist type theory is typed lambda calculus.
Types in a type theory allow for the avoidance of paradoxes for their use in formal logic. What must be noted is that the Curry-Howard isomorphic reveals that computer programs are mathematical proofs.
Simply typed functional programming languages such as Adga are guaranteed to always terminate which completely solves the halting problem. Tauchain in specific utilizes dependent types and there are major benefits to this when you realize the importance of type safety and type checking.
Dependent types depend on values. In Agda which is an example of a dependently typed functional programming language allows you to include values inside types. Dependent types are value dependent. To give an example of a dependent type which anyone can understand I will use a natural language example.
In natural language we have a concept called months. Months contain days and are a group of days. The amount of days in a month varies from year to year and from month to month. Days can be considered a data type. For any month m, there is a type (or set) D(m). D(m) of the days in that month.
So for any month m, we have a type D(m). Of course this is an extremely simplified example because not every month has the exact same number of days but in general a month is a set of days and type D is an example of a data type for days. D is a type which depends on the month and the year because different months have a different amount of days and also there are leap years. Any family of sets indexed by another set is a dependent type and these are everywhere if you look carefully.
Programs as Proofs
Proof by construction is also called a constructive proof. A constructive proof contrasts with existential proofs by demonstrating the existence of the mathematical object.
A proof of a proposition is a judgment. A program as a proof reveals that logic and programming are isomorphic. If you're doing programming then you're doing logic. In Tauchain you will be able to take advantage of the Curry-Howard isomorphism and intuitionist type theory to work with all forms of knowledge and do mathematics.
Martin Lof type theory / intuitionist type theory is at the foundation of the Tau compiler. Tau will be fully compatible with this when completed which will allow a programmer to have all of the fantastic benefits provided by Martin Lof type type / intuitionist type theory. Homotopy type theory is a related idea which may reach a convergence Tauchain.
The relation between type theory and category theory
There are correspondences between type theory and category theory. Cartesian closed category for example corresponds to Martin Lof type theory and to typed lambda calculus. These relations go quite a bit deeper than this but I will not go too deep into it because my background is not in mathematics. At the same time perhaps it could be said that if you're a programmer then you are a mathematician and that hints at the foundation of these correspondences.
Category theory works on several components. In particular a category is a mathematical structure like a group of vector space abstractly defined by axioms, and in category theory there is a concept called morphisms. A morphism is a structure preserving map from one mathematical structure to another. A function is considered to be a morphism for example.
Simplification of Proofs as Evaluation of Programs
How do you evaluate how a program will function prior to running it? In Tau you will be able to reason over the code and evaluate it for a proof of correctness. Languages such as Agda use dependent types which are types which depend on values or terms. More on this topic can be discussed further at a later date.
Conclusion
I hope I provided an introduction to some of the deep concepts behind Tauchain. Computational trinitarianism is propositions as types, programs as proofs, and the relation between type theory and category theory. Curry-Howard isomorphism is what makes computational trinitarianism possible by revealing that programming is logic. Martin Lof type theory/intuitionist type theory is at the heart of Tauchain and allows Tau to deal with any kind of knowledge.
References
- https://ncatlab.org/nlab/show/propositions+as+types
- https://en.wikipedia.org/wiki/Curry%E2%80%93Howard_correspondence
- https://en.wikipedia.org/wiki/Agda_(programming_language)
- https://mathoverflow.net/questions/208091/what-does-simplification-of-proofs-as-evaluation-of-programs-mean
- https://link.springer.com/article/10.1007%2Fs11225-006-6604-5
- http://learnyouanagda.liamoc.net/pages/introduction.html
- https://ncatlab.org/nlab/show/Martin-L%C3%B6f+dependent+type+theory
- https://www.cs.cornell.edu/courses/cs312/2004fa/lectures/lecture9.htm
- https://en.wikipedia.org/wiki/Type_theory#Relation_to_category_theory
- https://en.wikipedia.org/wiki/Morphism
- https://en.wikibooks.org/wiki/Category_Theory#What_is_a_category.3F
- https://golem.ph.utexas.edu/category/2010/03/in_praise_of_dependent_types.html
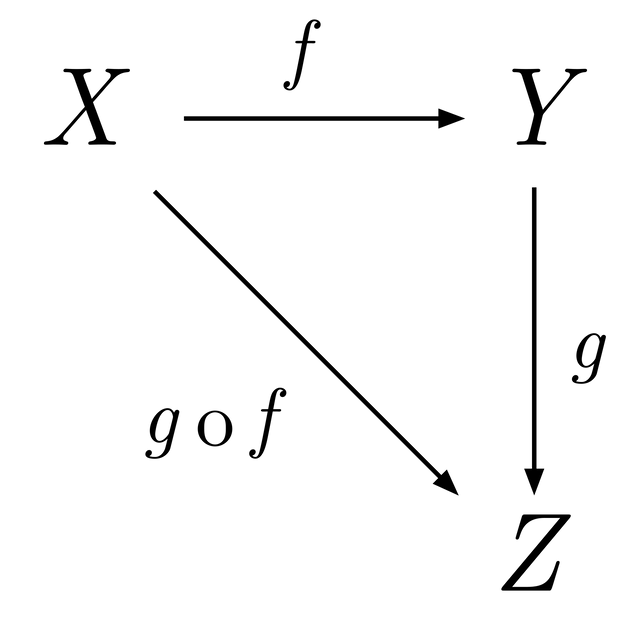
So, does Tau independently implement an automated theorem prover as part of its protocol?
Only as part of the client. It's not part of the protocol itself. Furthermore, Ohad insists the Tau autoprover will be state of the art.
What are the atomic symbols in the autoprover?
Ohad states: "just like notation3 reasoners (see dana's previous post). only on tau rdf's type system is augmented with mltt."
For me, this aspect is the very essence of TauChain . In one of your first posts you wrote:
So Tau offers a guarantee that the code will fulfill the specification - that's great and I understand it. But what will guarantee that my plain English description is translated by a mathematician into a specification without any errors or omissions? Don't we just move the problem one level up?
Also, have you got any example of a formal spec for a piece of code to be written in Tau or any other provable language? it's hard for me to imagine what it looks like.
From my understanding of what is planned there is a developer or two who will be working on a controlled natural language. Attempto Controlled English (ACE) will allow implementation of something like Attempto for example.
and...
So while not straight up English it will be a controlled English which means anyone who can speak English should have no problem dealing with it.
References
I was about to getting excited about this project but then I've found that their Github repo didn't update for about a year. I hope these ideas will come to life some day.
It was last updated in May. I don't know where you see a year but look at the commits: https://github.com/naturalog/tauchain/commits/master
Development is not going to be fast until the compiler is complete and the compiler has to be correct by construction. It cannot have a bug and must be built in the formal way. In addition, it must be as optimized as possible. The developer is working with all of the state of the art concepts and ideas so it's something which can't be developed any faster no matter how much money you throw at it or how many Phds you have.
But I do think once the compiler is complete then anyone will be able to join in and development will be significantly faster. The question of how long it will take to complete the compiler is anyone's guess but only Ohad has any idea. I thought it would be completed by now but the only answer I can give now is as long as it takes to get it done right.