En primer lugar mis saludos respetuosos para toda la comunidad de steemit, continuando con la temática geometría analítica plana, en donde seguimos dando importantes pasos para la comprensión analítica de las matemáticas, en esta oportunidad estudiaremos a la parábola, por lo tanto, conoceremos la determinación de sus ecuaciones, con esto seguimos con el análisis detallado de las ecuaciones y los lugares geométricos de una curva específica, determinando de esta manera sus propiedades particulares.

En la pasada publicación analizamos a la circunferencia, hasta ahora hemos estudiado a la línea recta y circunferencia, representando ambas dos líneas o curvas conocidas por los estudiantes, pero el objetivo es seguir brindando a ellos el aspecto analítico de otras curvas para la mejor interpretación y comprensión de las mismas.

Introducción

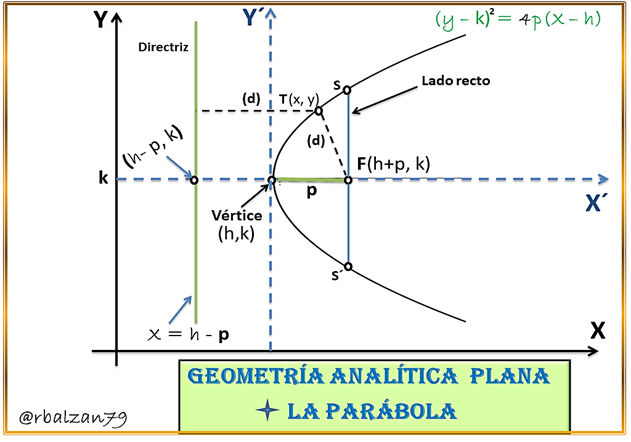
En base a lo desarrollado con anterioridad, el aspecto analítico desde el punto de vista de la geometría plana en cuanto a las líneas o curvas ya analizadas, nos permite expresar que la parábola es aquel lugar geométrico, en donde, un determinado punto tiene movimiento en el plano de tal forma que su longitud a una recta inmóvil (directriz), será siempre la misma a la distancia a un punto fijo (foco) del plano, y este punto no pertenecerá a dicha recta, antes de entrar en mayor detalle mostraremos la siguiente figura para poder tener mayor ilustración sobre el aspecto conceptual de esta curva:

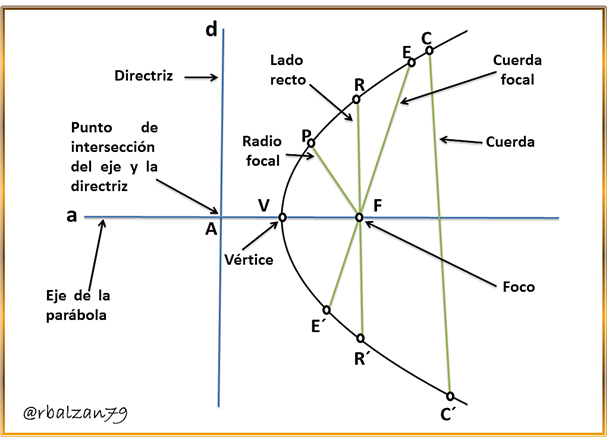
En la anterior imagen se observar los elementos presente en la conformación del lugar geométrico de una determinada parábola, con lo cual damos paso a la determinación de su ecuación.

Ecuación de una parábola con vértice en el origen y su respectivo eje focal, coincide con un eje coordenado

Mediante esta condición, la cual nos indica que el vértice de una determinada parábola está en el origen y el eje de la misma tiene coincidencia con uno de los ejes del plano coordenado, para ello, la ecuación de una parábola tendrá su forma más sencilla o simple, es decir, su forma canónica, como ya determinamos en la pasada publicación sobre la circunferencia, esto se debe a que dicha expresión representa el ejemplar más simple de la ecuación de una determinada curva, que en este caso es para una parábola.

Iniciaremos considerando la siguiente imagen , para realizar nuestro análisis:

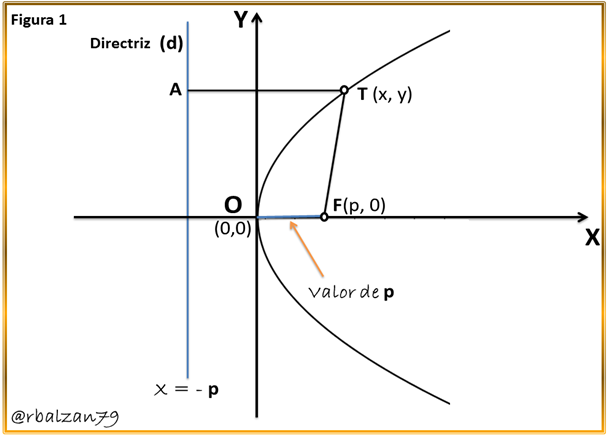
De forma general supongamos una parábola cuyo vértice se encuentre en el origen (0,0) y su eje coincide con el eje X, como observamos en la imagen anterior.

Para este caso tendríamos un tipo de parábola que estaría abriéndose o mirando hacia el lado positivo del eje X, podemos hacer referencia que dicha abertura dependerá del valor de (p), en donde, (p) representa la distancia del vértice al foco de la parábola, y el mismo pudiera ser positivo o negativo, para el presente caso dicho valor (p) es positivo, es por eso que la parábola de la figura 1; abre hacia el lado derecho del eje X, y si (p) es negativo abrirá hacia el lado contrario, es decir, izquierdo del eje X, por lo tanto, tenemos que el foco de dicha parábola se encuentra en el eje X, y sus coordenadas serán (p , 0) recordando la definición antes descrita de parábola, tenemos también que la ecuación de la directriz (d) será x = -p, para el caso expresado en la anterior figura. Observamos un punto cualesquiera de la parábola el mismo es T(x,y), dicho punto puede estar en cualquier lugar de la parábola, pero lo que por definición debe cumplir o satisfacer este punto es la siguiente condición geométrica:

Para lo cual sabemos según la fórmula de la distancia entre dos puntos en el plano F (p, 0) y T(x, y) que:

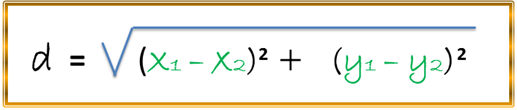
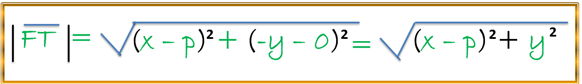
Tenemos que:

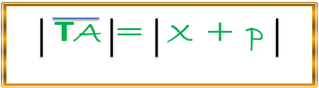
Con esto podemos formular analíticamente la condición antes descrita (FT = TA) de la siguiente manera:

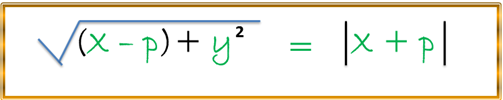
Para poder determinar la ecuación de la parábola en forma más simple, resolvemos en primer lugar elevando al cuadrado ambos miembros para luego simplificar dicha ecuación arriba planteada, por lo tanto, tenemos:

Siempre es importante recordar que si p>0 , la parábola se abrirá hacia la derecha, si por el contrario p<0 dicha parábola se abre hacia la izquierda, si el eje de la parábola coincide con el eje Y y con vértice en el origen tendríamos que la ecuación será:

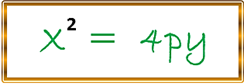
Las coordenadas del foco son ( 0, p ) y la ecuación que representa a la directriz será y= -p, en donde, la parábola abrirá hacia arriba si p>0, pero si p<0 dicha parábola abrirá hacia abajo, para ambos casos mediante el valor absoluto del coeficiente del término de primer grado, es decir, 4p, podemos determinar la longitud del lado recto de dicha parábola.

Ejercicio 1

Hallar la ecuación de una parábola, las coordenadas de su foco, la ecuación de su directriz y la longitud de su lado recto, sabiendo que su vértice se encuentra en el origen y su eje focal coincide con el eje X , la misma pasa por el punto (-1 , 3).

Con los datos antes mencionados ahora lo aplicamos a un plano cartesiano para ir verificando los mismo y poder analíticamente lograr determinar la ecuación de dicha parábola, entonces, tenemos lo siguiente:

Recordemos que el valor de p, nos indicará para donde abrirá la parábola, esto lo podemos observar al momento de graficar dicha curva, con la ayuda de la aplicación GeoGebra realizamos la siguiente imagen:

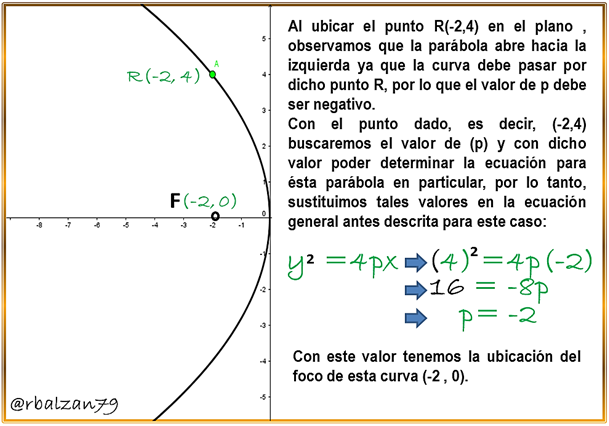
A continuación los elementos solicitados según las condiciones dadas en nuestro ejercicio:

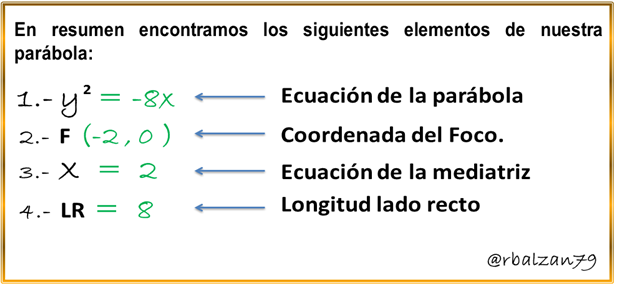
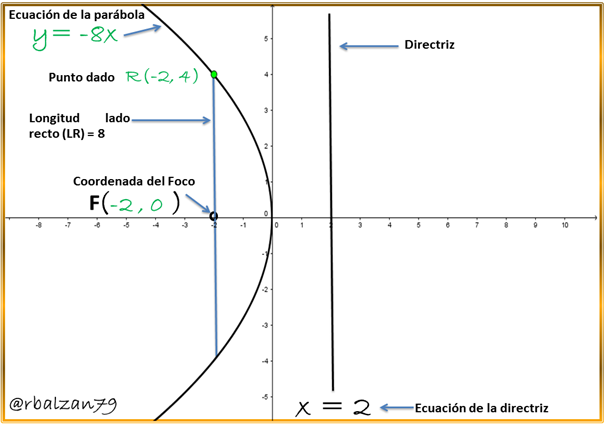
Tales elementos se muestran en la siguiente imagen:

Ecuación de una parábola de vértice (h , k) y eje focal paralelo a un eje coordenado

Ya conocimos la ecuación de una parábola cuyo vértice era el origen del plano cartesiano y su eje focal coincidía con algunos de los dos ejes coordenados, pero por lo general nos podemos encontrar con una parábola cuyo lugar geométrico tenga una ubicación distinta a la antes planteada, por lo que se hace necesario determinar para este tipo de caso la ecuación respectiva de dicha curva, en donde, su vértice sea distinto a la del origen y su eje focal sea paralelo a cualquiera de los dos ejes del plano coordenado, entonces consideremos la siguiente parábola cuyo vértice será el punto (h , k) y su eje focal es paralelo al eje X, como se muestra en la siguiente imagen (apoyada en la aplicación de GeoGebra), para este análisis:

Se observa en la anterior figura el traslado de un nuevo sistema de coordenadas X´ y Y´, en donde, ambos ejes son paralelos a los ejes coordenados originales o patrones, en este nuevo sistema el origen O´ va a coincidir con el vértice (h , k), por lo tanto, utilizando la expresión que ya hemos determinado como primera ecuación ordinaria o canónica tenemos:

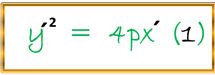
En donde, tomando en cuenta las condiciones para traslación de los ejes coordenados de un plano tenemos, cuando trasladamos los ejes de coordenadas a un nuevo origen, es decir, O´(h , k), y si tenemos que las coordenadas de cualquier punto (P) antes como después de dicha traslación son (x , y) y (x´ , y´) , proporcionalmente, asumimos que las ecuaciones de transformación resultantes del sistema original al nuevo sistema de coordenadas serán:

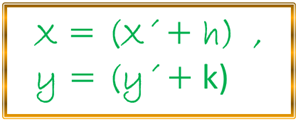
Expresado lo anterior, despejando (x´, y´), luego sustituimos dichos valores en nuestra ecuación (1), nos queda:

Ejercicio 2

Hallar la ecuación de la parábola cuyo vértice lo representa el punto (3 , 2) y pasa por el punto (5 , 4) y su eje focal es paralelo al eje X, encontrar también, la ecuación de la directriz, coordenada del foco y longitud del lado recto.
Debemos recordar el traslado de los ejes originales como se mencionó anteriormente, por lo tanto, la ecuación a utilizar según las condiciones antes descritas es:

Con el punto dado de nuestra parábola T(5 , 4) y las coordenadas del vértices V(3 , 2) sustituimos en la ecuación (2), para poder encontrar el valor de p ( distancia focal):

Ahora con este valor p = ½ y el vértice (3 , 2) sustituimos en (2) para encontrar la ecuación de la parábola planteada:

La ecuación antes descrita la podemos desarrollar y nos queda de la siguiente manera:

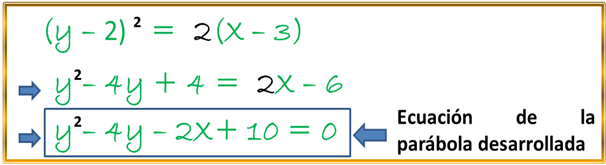
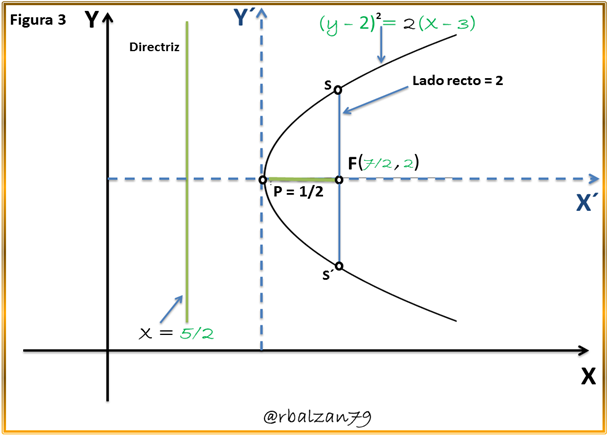
Luego de mostrar la forma desarrollada de la ecuación ordinaria de nuestra parábola, buscamos la ecuación de la directriz, coordenada del foco y longitud del lado recto:

En la siguiente imagen (con apoyo de la aplicación GeoGebra) se muestran cada uno de los elementos encontrados:

Conclusiones

1.- A medida que avanzamos con el análisis de estas curvas bases, podemos observar que es necesario los conocimientos de las pasadas curvas, es decir, vamos logrando una comprensión de forma analítica de manera consolidada, ya que estamos desarrollando las bases necesarios para la comprensión de cualquier tipo de curva y en las distintas dimensiones que se encuentren, hacia allá vamos partiendo de lo más simple a lo más complejo como es el camino para la obtención de cualquier aprendizaje del ser humano.

2.- Para esta publicación analizamos a la parábola mediante la determinación de sus ecuaciones más elementales, con las cuales pudimos encontrar su lugar geométrico y estudiar los elementos que en dicha curva se encuentran, elementos importantes como la longitud o distancia focal (p), la misma nos permite establecer de manera práctica y rápida la abertura de una parábola, en las distintas condiciones que se nos plantee resolver el lugar geométrico de esta curva, por lo tanto, si queremos conocer la orientación de una parábola todo dependerá del valor de p, recordando siempre que este valor (p) representa la distancia del vértice al foco de la parábola, por lo tanto, si (p) es positivo, es decir, p>0, la parábola abrirá hacia el lado derecho del eje X, y si p es negativo abrirá hacia el lado izquierdo del eje X, de la misma forma podemos analizar la orientación de esta curva con respecto al eje Y, bien sea hacia arriba (p>0) o hacia abajo (p<0), tomando en cuenta el análisis del signo de p.

2.- Las ecuaciones de las parábolas cuyos vértices sean el punto (h , k) y ejes focales paralelo a cualquiera de los ejes del plano coordenado, también las conocemos como segunda ecuación ordinaria para este tipo de curvas. Hasta ahora nos hemos dado cuenta que siempre será de vital importancia comprender las raíces de un determinado conocimiento, esto permitirá que cualquier persona sea capaz de intuir la razón de aprender adecuadamente.

Nota: Todas las imágenes fueron elaborados usando las aplicaciones Paint, Power Point y GeoGebra.

Referencias Bibliográficas

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

Autor: @rbalzan79