ARCHIMEDES' PRINCIPLE AND PRINCIPLE OF FLOATATION

The Archimedes' principle and the principle of floatation get people confuse. Are these two principles the same or different? This has been a critical question people do ask. What makes a gigantic structure like a ship to float on the sea is another mystery. I also use to imagine how a ship of hundreds of pounds in weight floats on water considering how heavy the loads it carries while even half weight of the load will sink if thrown overboard.

In Olympic swimming competitions, it is possible to swim across a pool floating if you stretch your body out flat on the water to establish equilibrium, but the same individual will sink if the arms are wrap around the legs and curl up into a ball. The reason for this occurrence is made possible due to the fact that floatation has to do with how much water is pushed against the immersed object. This phenomenon can be simply explained by Archimedes’ principle.

Law of flotation is simply the application of Archimedes' principle. Archimedes made the first hypothesis about the relativity of displacement and density of the matter immersed. It was verified before making it a principle.

Archimedes’ principle referred to as the physical law of buoyancy was discovered by the ancient Greek inventor and mathematician known as Archimedes. The principle states thus; the exerted upward buoyant force on a body fully or partially immersed in a fluid is equal to the weight of the fluid displaced by that the body acting in the upward direction at the center of mass of the displaced fluid. This principle explained that the volume of displaced fluid is equivalent to the volume of an object fully immersed in a fluid or to that portion or fraction of the volume immersed for an object partially submerged in a liquid since the density of the fluid is constant.

This can be illustrated mathematically using the equations below:
Weight = Mg; where M implies mass of an object and g is acceleration due to gravity, g is a constant.
Mass = density x volume
Simply put,
Weight = density x volume x g

Buoyancy; By Khursheed afroz - Own work, CC BY-SA 4.0,

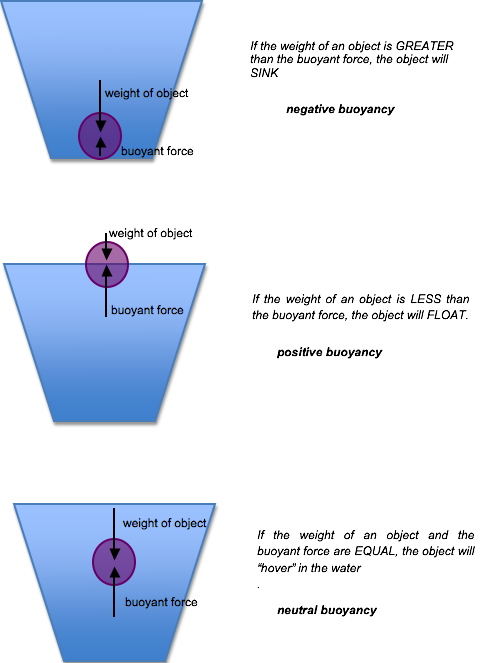
By implication, the difference between the buoyant force and its weight is the net upward force on the object. This net force could be positive, negative or neutral (zero), the object floats if the net force is positive, the object sinks if negative and if zero (neural), the object is neutrally buoyant which makes the object remains in place without either rising or sinking.

The basics of naval architecture for ship design and construction was found in Archimedes’ principle. The weight of a floating object (static) must be equal to the weight of the volume of water that is displaced by the object. This law of buoyancy explains both the draft at which a vessel moves on water and the angles that it assume at equilibrium with the water. When an object heavier than the amount of the fluid it displaces is released in water, it will sinks.

For instance, when a ship is launched, it sinks into the ocean unless the weight of the water it displaces is just equal to its own weight. As more load is added to the ship, it sinks deeper, whereby displacing more water, so, the magnitude of the buoyant force will continually matching the weight of the ship plus its cargo. Literally, the size of that ship is a function of the volume of displaced water by a ship, also, in turn, the ship’s size depends on the weight of water that is to be matched by displacement. Ships are designed to carry a specified weight of cargo, including some needed supplies such as lubricating oil, fuel, crew, and some other first aids and some life aiding equipment.

All these forms of weights are combined to form a deadweight. The deadweight, and all other weight that contributes to the shipping weight are categorized as lightship weight. Displacement is referred to the weight of displaced water which must be equaled to the weight of the ship for it to float is the sum of deadweight and lightship weight.

By MC3 (SW/AW) Casey J. Hopkins

Ship Stability relative to Archimedes’ Principle
To achieve great ship stability, many items contributing to the weight of the ship must be distributed with a considerable precision. Uneven distribution of item weight contributes ship instability and bad inclination, which makes the ship to float in an unwanted angle of heel and trim referred to as sideways and endwise inclination respectively. Archimedes’ principle to the first moments of weights and volumes ensured to avoid such inclinations. The two main problems of stability are attributed to Nonzero heel angle and Nonzero trim angle.

Nonzero heel is considered more dangerous, because of the sideways inclination, it makes all activities and routines on board very difficult, also it enhances the possibility and margin of capsizing. During heavy weather, nonzero trim angles could enhance the possibility that the bow will slam into waves, it may also cause the tips of propeller blades to stay above the water surface.

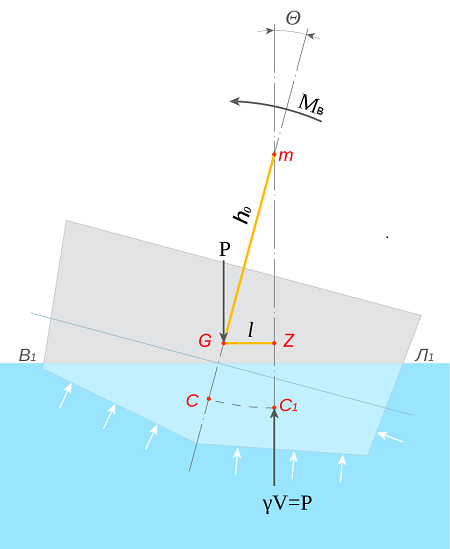
Static stability of ship ;By Maxrossomachin - Own work, CC0,

For a ship at rest in still water, there are two vertical forces always act upon the ship; its weight (W) and displacement (D). The weight acts downwards through the centre of gravity (G), and the displacement (D), acts upwards through the centre of buoyancy B. The magnitude of both the weight and the displacement are always an equal and same line of motion in order to maintain the body at equilibrium. For the ship to be in equilibrium, the sum of their moments must be zero. The moment will act in the stable direction, as long as the point M is above G, point M is the point where the midplane intersects the buoyant force where G is the centre of gravity of the ship and its contents.

The angle of heel tends to increase by the forces of weight and buoyancy, if M is below G, the equilibrium will be unstable. The transverse metacentric height is the distance from G to M, taken to be positive if M is above G. The stability of a ship under most conditions is designed to be able to overcome any form of restriction or resistance that may be encountered during a heavy storm in the sea, nevertheless, ships possess undesirable roll characteristics when the balance of oscillations in roll is twice that of oscillations in heave, thus capsizing is inevitable

Summary

Law of flotation is simply the application of Archimedes' principle. The fundamentals of naval architecture are found in Archimedes’ principle. An extension of Archimedes’ principle to the first moments of weights and volumes is ensured to avoid nonzero trim and nonzero heel inclinations in ship design and construction. The first weight moment of the water displaced must be equal to the collective first moment of all weights for a ship to float.

Thanks for visiting my blog
Note: All Images are from free sources

REFERENCES

https://www.quora.com/What-is-the-difference-between-archimedes-principle-and-principle-of-floatation
https://www.britannica.com/science/Archimedes-principle
https://www.britannica.com/technology/ship#ref528206
https://en.wikipedia.org/wiki/Archimedes%27_principle
https://physics.weber.edu/carroll/archimedes/principle.htm