Transient In Electrical Circuits.

fona (55)in #stemng • 6 years ago (edited)

Transient is a period of disturbance in an electrical circuit, in which the circuit is needed settle from it's disturbed state to a steady state. Transient disturbance is caused as a result of switching on and off of electrical circuits. It usually lasts for about few tenth of a second.
In analysing circuits under transient, the voltage and current level consist of two parts;

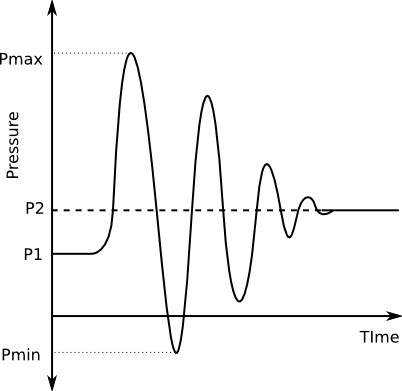
1 The transient part.

2 The steady state part.
I= I1 + I2
where I1= the transient current
where I2= the steady state current.
The steady state value is obtained by ohms law.
The transient solution are usually obtained by solving differential equations.
Transient is common in circuits with energy storing components such as a capacitor, or an inductor. Resistors do not store energy hence it's effect is only damping. Transient begins immediately the switch is turned on or off. This implies that, to obtain the solution to transient is by solving differential equations of the circuit if the given current and voltage are assumed as zero.
E.g
Ldi/dt + Ri......1
From the initial condition obtained from the circuit by ohms law, the steady state solution is obtained.
The general solution for the equation 1 is given as i=Ne^-mt
Where m= root of characteristic equation
N is a constant whose value is gotten by the initial consultations. That is t=~ or t=0.

First Law of Switching

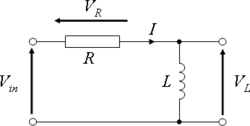
The first law of switching states that, the current flowing in an inductance can not be changed instantaneously. Meaning that the value of current in an inductor at a particular time, is the same as the initial value at the time of transient, which is also the same with the steady state value. Let us consider a circuit with a switch, a resistor, and an inductance. Before the switch is closed, Vr=0 Vl=0 These are the initial steady state condition. Once the switch is closed, the following begins; 1 transient begins. 2 current begins to rise from zero, and the value in Vr and Vl increases. Part of the voltage applied is developed across R and the other part balances the induced EMF in the coil. By kirchoff's law, V=Vr+Vl = Ir+Ldi/dt... (1) After switch is closed, and steady state is achieved, t=~ Rate of change for current di/dt =0, Vl=0 Therefore Vr=V and I2=V/R assuming that no transient and that dt=0 the current reaches maximum. Under this condition Vl=Ldt/dt=Ldi/0=~ thus the induced emf is infinite. This therefore contradicts the given condition where the applied voltage is a definite quantity Thus, after switching t=0, current in the circuit =0. That is; I=0, Vr=Ir=0 the inductance stimulates an open circuit hence the value of the voltage in the inductance can rise instantaneously.

second Theory of switching

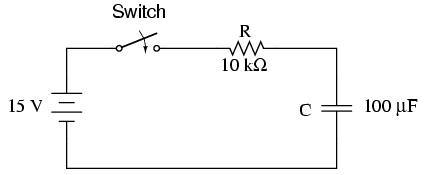
It states that the voltage across a capacitor can not change instantaneously. That is, the voltage of a capacitor at the beginning of the transient period is the same at the preceding steady state. Let us consider an R-C circuit connected to a DC source. Once the switch is closed, transient period begins. During this transient period the capacitor charges up. By kirchoff's law, V=Vc+Vr=Vc+Ir..... (2) In a capacitor I=dq/dt=CdVr/dt V=Vr+Rr(CdVr/dt)...... (3) Part of the applied voltage is on R while the other part helps to balance the voltage in the capacitor. In steady state condition t=~, the capacitor charges up to Vc=V and this means that Vc is constant and I = C.dVc/dt=0 thus voltage drop across the resistor is zero. Hence the applied voltage is on the capacitor. If Vc is to change instantaneously dt=0, I=C.dV/dt=~. When t=0 there would there would be an infinite value of voltage, there by contradicting the finite value of voltage. An instantaneous change in the voltage across the capacitor would mean that the electric field will increase from 0 to another value Wc=CV^2/2. This kind of change can only be possible if an infinite source is connected to the capacitor, which is physically not yet achievable.

Conclusion.

The value of the voltage across capacitor at the beginning of transient period is zero. The capacitor stimulates short circuit, the voltage drop across the resistor is equal to the applied voltage which is the initial condition of the circuit. Thus the current in a capacitor can however change instantaneously.