Mathematical collision on the analysis of Integral

Image elaborated and edited for @centaurox.
A few of these mathematical applications as tool it is the integral, which under the scheme of the theory of integration presents two principal aspects, the calculation of integrals of functions and the second one the measurement of set. From the point of view the calculation of the area, which encouraged the development of the integral calculus, which was used to simplify and to verify equations at level of the physics, chemistry, biology, up to the economic world, which allowed to define equations for the operations, to obtain the integrations of joint equations, under the approach of method of integration.
The definite definition of the integral was consisting of using a process of limit, to assign measurements to quantities as area, volume, etc. For the definition of double integral of a function of two variables in a region of the plane, a similar process will be used, dividing the region in subregions and taking the limit when the number of subregions is infinite.
The previous process of iterated integration, with the correct definition of the limits of integration, as be the enclosure of definition, it will be the one that is used for the calculation of the integral double ones.
Textual appointment of the book, Integral calculus for José Manuel Casteleiro, Rafael Paniagua Gómez-Álvarez
pág .:425.
Analysis across a graph.
The exposition is the following one it is a question of finding tangent in a point of a curve C, considering a function f continues and print, having knowledge the following relation x = to, x = b.
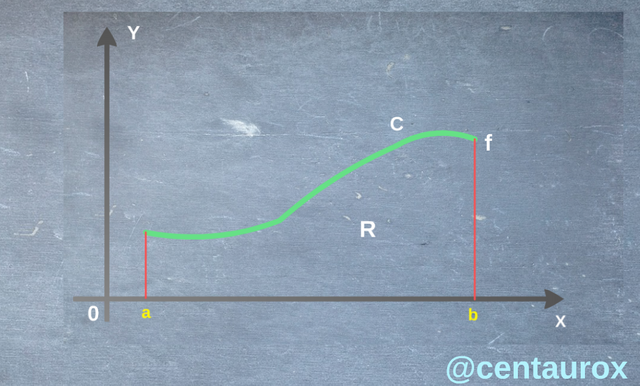
Graph 1 prepared one for @centaurox.
In this graph it shows us that the region R shut up between the curve C, the axis of the abscissas and the straight lines of equations, x = to, x = b possess an area, which measures a number of square units, which are inside the region, when there takes for unit the area of the square of side for the close one, our limitante is the region in R it is limited by a curve. Considering f a function it continues and defined in [to, b] be f> the (x)th 0, taking the axis of the abscissa as a reference 0X and the straight lines of equations, x = to, x = b, in such a way that we divide the segment [to, b], in equal lengths of b-a/n, giving several rectangles it has as base of a segment of length (b - to).
Of such form we have the height of length f (x0), f (x1), f (x2), f (x3), f (x4), f (x5), f (x6), separate we have the following relation in n, the segments of equal length b-a/n, where it is considered to be the distance of to up to b having as segment of ends taking in account the points to of starting point to (b - to)/n up to considering to k (b - to)/n and this one in turn establishes the relation according to the Xth = to (b - to)/n, for every segments, that we consider in a particular division of the segment [to, b], for this case n=6, the obtained rectangles.
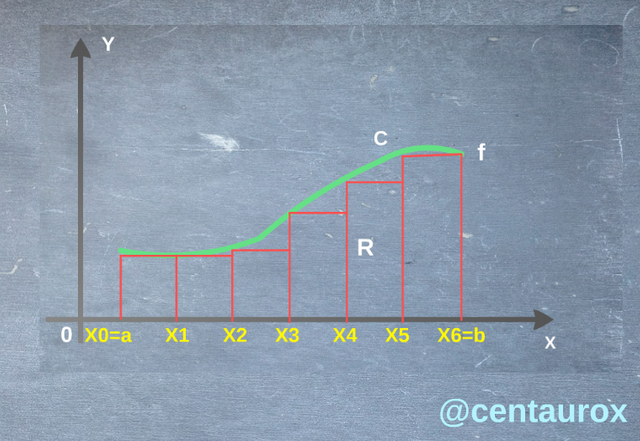
Graph 2. It is possible to appreciate that to measurement, that the breadth of the rectangles comes closer zero, the rectangles more it comes closer the curve, from what the sum of his areas approaches more the area under the curve in C, considering f the (x)th is positive and to <b. (Prepared for @centaurox)
Use for for sum of the areas the letter T6, to have the following resultant one:
T6 = (b - to)/6f (x0) (b - to)/6f (x1) (b - to)/6f (x3) (b - to)/6f (x4) (b - to)/6f (x5) =
Establish the following equation.
(b - to)/6 [f (x0) f (x1) f (x2) f (x3) f (x4) f (x5)] =
Tn = (b - to)/n [f (x0) up to coming to the expression f (Xn-1)]
The resultant one in Tn is the value of the area shut up by the region understood between the graph of f, the axis of the abscissas and the straight lines of equations x = x0, x=xn.
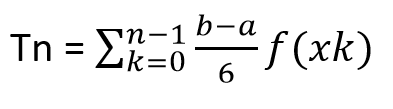
Conclusion.
It is very important to announce the application of the integral as mathematical tool, where it can help us to better it is possible to use to calculate areas between curves, volumes of solid, and the work realized by a variable force. In this case we are going to be emphasises on the calculation of volumes of occurred rarely cylindrical, on the other hand also it allows us in those sciences that it realizes estimations by means of projections, allows us to analyze in a qualitative way and quantitatively the different phenomena that present him to him in his daily environment, as the case of Economy and in Biology.
Consulted bibliography.
Hughes, applied Calculation, Mexico, CECSA, 2004.
Integral calculus - Page 425 for José Manuel Casteleiro? Rafael Paniagua Gómez-Álvarez - 2002.
Differential calculus And Integral - Page 226 - 2007.
Calculus. 1, Tom M. Apostle? Francisco Vélez Cantarell - 2005.
Beginning of mathematical analysis - Page 390 Enrique Linés Escardó - 1991.
