Aplicación de las Derivadas de Funciones de Varias Variables en la Optimización (Modelo de Mínimos Cuadrados)
Saludos estimados miembros de la comunidad científica de #STEM-ESPANOL, #STEM-STEEM y STEEMIT en general, después de cierto período de ausencia debido a problemas técnicos les comparto el día de hoy un artículo que aborda una de las aplicaciones de las derivadas de funciones de varias variables en la solución de problemas de la vida cotidiana.
La ciencia se esfuerza en estudiar y describir la realidad de forma precisa, desde la medicina hasta la física numerosas teorías permiten describir los fenómenos del mundo real y encontrar soluciones a diversas problemáticas mediante el establecimiento de modelos y teorías desde un enfoque científico.
En este orden de ideas, la matemática tiene innumerables aplicaciones en diversos ámbitos de la actividad humana, en las empresas y organizaciones en muchos casos se recolectan datos sobre multitud de variables relacionadas con sus operaciones, muchas veces estos datos son analizados en busca de patrones ¿Existen relaciones notables entre las variables estudiadas?, por ejemplo, al estudiar los datos sobre la demanda de un producto se puede construir una función de demanda en base a la naturaleza de los datos la cual suele expresarse en lenguaje matemático.
Ahora suponga que una empresa desea construir un aeropuerto que debe prestar servicio a 4 ciudades cercanas, estableciendo un eje de coordenadas dichas ciudades se ubican en los puntos (20,5) (0,30) (-30,-10) y (-5,-5) tal que las coordenadas representan los kilometros a partir del origen. ¿Cuál es el punto óptimo en el cual debe ubicarse el aeropuerto?
Gráficamente podemos utilizar la herramienta en línea www.desmos.com para visualizar los puntos en el plano cartesiano que representan las ciudades, para introducir los diversos puntos en esta herramienta se suelen separar con comas:
(20,5),(0,30),(-30,-10),(-5,-5)
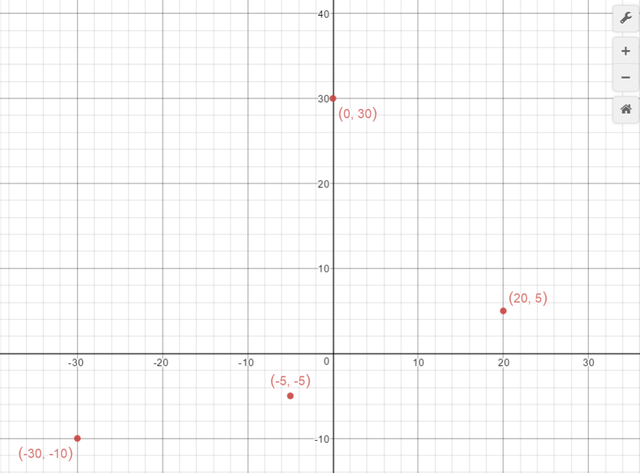
Imagen N° 1. Ubicación de las ciudades representadas en el plano cartesiano. Fuente: Elaboración propia utilizando la herramienta en línea www.desmos.com.
En la imagen N° 1 se puede apreciar la ubicación de los puntos en el plano cartesiano, la solución que se desea obtener será también otro punto en dicho plano.
El problema mencionado anteriormente puede ser resuelto planteándolo en lenguaje matemático para luego aplicar técnicas que permitan obtener su solución, sin embargo, surge la siguiente interrogante ¿Qué se considera el punto óptimo? Un criterio comúnmente usado en este tipo de situaciones es determinar la ubicación (x,y) que minimice la suma de los cuadrados de las distancias entre el aeropuerto y las ciudades.
Analizando el problema se observa que sus incógnitas son x y y debido a que se debe localizar el punto exacto donde ubicar el aeropuerto, se desea encontrar una expresión que represente el cuadrado de las distancias del aeropuerto a cada ciudad, lo cual se puede obtener mediante el teorema de Pitágoras, el cual plantea que:
Si se conocen dos puntos (x1, y1) y (x2, y2) y se desea determinar su distancia la misma se puede calcular mediante la siguiente expresión:
En base al teorema de Pitágoras se encuentran expresiones para el cuadrado de las distancias que separan las ciudades del aeropuerto y al sumar las correspondientes a los 4 aeropuertos se obtiene
Para encontrar los puntos críticos se determinan las primeras derivadas en función de x y de y
Igualando ambas derivadas a cero se obtienen los valores críticos
Luego para determinar la naturaleza del punto crítico se aplica la prueba del punto crítico la cual plantea que:
Si se tiene un punto crítico de f localizado en (x*, y*, z*) en que todas las segundas derivadas parciales son continuas, determine el valor de D(x,y), donde
- Si D(x*,y* )>0
El punto crítico es
a. Un máximo relativo si tanto fxx (x*,y*) como fyy (x*,y*) son negativas.
b. Un mínimo relativo si tanto fxx (x*,y*) como fyy (x*,y*) son positivas.- Si Si D(x*,y*)<0 El punto crítico es un punto en silla de montar.
- Si D(x*,y*)=0, se necesitan otras técnicas para determinar la naturaleza del punto crítico.
Se calculan las segundas derivadas en función tanto de x como de y
Se calcula el discriminante
Como D(x*,y* ) es mayor que cero y
Se trata de un mínimo relativo, gráficamente se puede observar la existencia de este mínimo relativo utilizando el Software Matemáticas de Microsoft
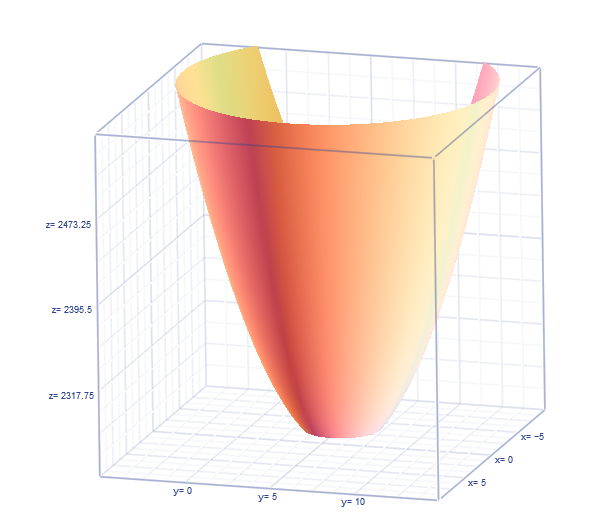
Imagen N° 2. Función Sumatoria de los cuadrados de las distancias mínimas de las ciudades al aeropuerto. Fuente Elaboración propia utilizando la herramienta Matemáticas de Microsoft.
En la Imagen N° 2 se puede observar la existencia del mínimo relativo el cual representa la solución buscada. Es decir, el aeropuerto debe ser ubicado en las coordenadas (-15/4, 5), este punto puede ser observado en la imagen N° 3
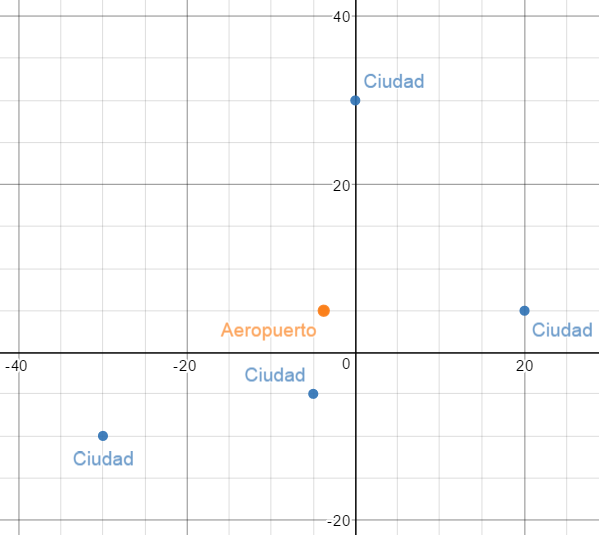
Imagen N° 3. Ubicación del aeropuerto y las ciudades en el plano cartesiano. Fuente Elaboración propia utilizando la herramienta en línea desmos.com.
En este punto la suma de los cuadrados de las distancias del aeropuerto a las ciudades es de
Es decir, la sumatoria de los cuadrados de las distancias de las ciudades al aeropuerto es de 2218,75.
De esta forma se puede apreciar como utilizando las herramientas del cálculo diferencial en varias variables se puede abordar este tipo de problemas de optimización.
CONCLUSIONES
Las funciones de varias variables pueden ser utilizadas para modelar fenómenos referentes a la ubicación de puntos en un plano con el fin de encontrar el punto óptimo desde el cual se puedan alcanzar los demás puntos de forma eficiente.
La prueba del punto crítico es de gran utilidad en problemas de optimización, sin embargo, en el caso de que el discriminante sea cero se requieren otras técnicas para resolver el problema, las cuales serán abordadas en futuros artículos.
Los Softwares Matemáticos permiten visualizar mejor los resultados obtenidos de forma analítica, mejorando el proceso de aprehensión del conocimiento.
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editoria Limusa Willey.
Budnick (2007) Matemáticas aplicadas para administración, economía y ciencias sociales. 4ta edición Editorial Mc Grall Hill.
Si deseas leer contenido científico de calidad en habla hispana te invito a revisar la etiqueta #STEM-ESPANOL donde podrás encontrar diversidad de temas, Matemática, Física, Química, Biología, Medicina, entre otros.
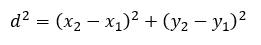
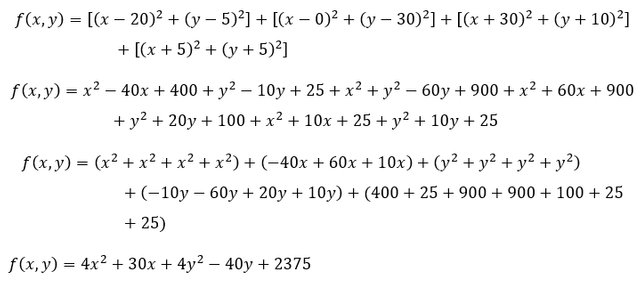
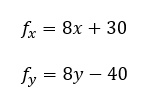
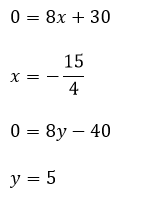
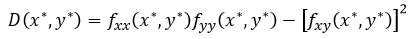
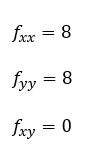
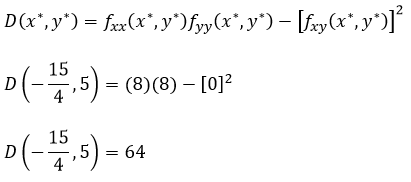
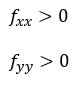
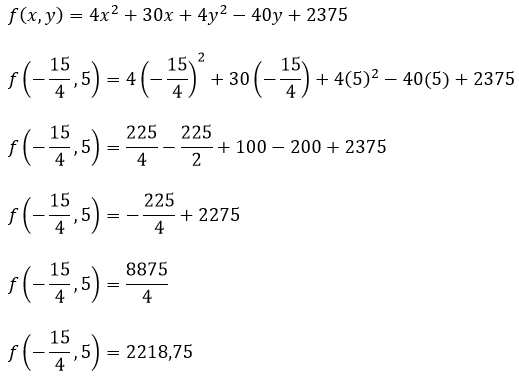
Excelente artículo. Te felicito también por las imágenes, que ayudan mucho al lector a tener una visión general del problema y solución.
Gracias @jga, así es, sobre todo en el caso de funciones en varias variables, te agradezco el apoyo que siempre me brindas.
Yes, the optimal point can be achieved, the trick is always how few points are needed. Of course, if you have data with stochastic noise, then exactly how accurately you can determine the optimal point is also in question. This all becomes much trickier when your surface has odd textures, or a long valley structure within it.
Muy buen artículo sobre la aplicación de las derivadas @ydavgonzalez, muy didáctico y muy bien presentado. Gracias por compartirlo. En mi blog tengo un post sobre La Definición de El Tiempo, podría interesarte. Saludos.
Gracias por el apoyo, ya lo revise, tienes mi upvote, Saludos @tsoldovieri.
Usted es genial en su área, lo felicito sinceramente @ydavgonzalez
Muchas gracias @morita.
Gracias por compartir este artículo, interesante e ilustrativo..
Gracias a usted por el apoyo, saludos @xeliram.
Excelente contenido. Gracias !
Gracias por apoyarme @carybe1969.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @ydavgonzalez!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Excelente material, te aplaudo.
Gracias @dcamachopt por tomarte el tiempo de leerlo.