APLICACIÓN DE LA INTEGRACIÓN DEFINIDA EN EL CÁLCULO DEL TRABAJO REALIZADO POR UNA FUERZA VARIABLE (PERSPECTIVA ANALÍTICA Y NUMÉRICA)

Imagen de Dominio Público Licencia CC0. Autor: Gerd Altmann
Disponible en el siguiente enlace.
Hola apreciados lectores de #stem-espanol, #steemstem y de Steemit en general, en mis artículos previos he abordado algunos de los modelos matemáticos que pueden ser aplicados en la ciencia, en el presente artículo me enfocaré en explicar una de las aplicaciones de la matemática en el estudio de los fenómenos físicos, de esta forma se podrá evidenciar como se conjugan estas dos ciencias para ir de lo abstracto a lo concreto.
La matemática es la ciencia de lo abstracto, de los modelos formales, de las realidades idealizadas, de las estructuras algebraicas definidas mediante un lenguaje muy preciso que poseen cierta belleza estética en sus planteamientos, sin embargo, sin la aplicación a realidades concretas la verdad matemática sería solo estructuras formales en la mente de los individuos.
En este orden de ideas, muchas veces los estudiantes del cálculo infinitesimal suelen preguntarse cual es la razón de aprender los procesos de derivación, integración, resolución de ecuaciones diferenciales y muchos otros procedimientos matemáticos; por esta razón la aplicación de los conceptos matemáticos a fenómenos del mundo real permite una mejor comprensión de estas estructuras abstractas al relacionarlas con situaciones que sean significativas para las personas.
Uno de los conceptos más importantes en el cálculo infinitesimal es la noción de integral definida la cual posee un gran número de aplicaciones en la ciencia e ingeniería, en el presente artículo se estudiará una de estas aplicaciones desde dos perspectivas que permiten abordar este tipo de problemas la perspectiva analítica y el enfoque numérico.
La física es una de las ciencias que provee gran cantidad de fenómenos en los cuales la matemática puede ser aplicada, tal es el caso del concepto físico de “Trabajo” y sus implicaciones en la dinámica del movimiento, en primer lugar haremos uso de la definición de trabajo planteada por Resnick, Halliday y Krane(1993), los cuales definen al trabajo W efectuado sobre una partícula como:
“El producto de la magnitud de la fuerza F y la magnitud del desplazamiento s a través del cual actúa la fuerza”
Es decir:
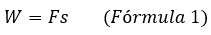
Básicamente lo que esta definición quiere decir es que el trabajo W es equivalente a la fuerza necesaria para desplazar una partícula multiplicada por la distancia a la que se ha desplazado dicha partícula, en el Sistema Internacional de Unidades (SI), la fuerza se mide en newtons (N) y la distancia se mide en metros (m), debido a esto la unidad en la que se mide el trabajo es el newton-metro (N·m), la unidad newton-metro también suele denominarse joule (J).
La fórmula 1 permite calcular el trabajo efectuado por una fuerza sobre un objeto, esta expresión es de gran utilidad, sin embargo, solo puede ser utilizada cuando la fuerza que realiza el trabajo es constante a lo largo de todo el desplazamiento del objeto, debido a esto si queremos determinar el trabajo realizado por una fuerza variable, debemos deducir un procedimiento que permita calcular el valor del trabajo W en función de la fuerza variable.
En este orden de ideas, si la fuerza es variable en lugar de usar una constante la expresaremos como una función de x, es decir, la fuerza se expresa como:
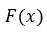
Supongamos que un objeto se mueve en dirección positiva a lo largo de un eje de coordenadas mientras actúa sobre él una fuerza variable F(x) que es aplicada en la misma dirección del movimiento, se desea determinar una expresión que permita calcular el trabajo efectuado por la fuerza necesaria para desplazar el objeto desde x=a hasta x=b.
Asumiendo que se descompone el intervalo [a,b] en pequeños subintervalos en los cuales la fuerza no varía mucho. De esta forma la fuerza en cada subintervalo puede ser considerada como una constante y se puede utilizar la fórmula 1 para calcular el trabajo en cada subintervalo, luego se realiza la sumatoria de los trabajos realizados en cada subintervalo, obteniendo como resultado el trabajo total realizado.
Matemáticamente podemos expresar este hecho dividiendo el intervalo [a,b] en n subintervalos insertando los puntos x1, x2 ,…, xn-1 entre a=x0 y b=xn.

Partición del intervalo [a,b] en n subintervalos. Fuente: Elaboración propia.
Ahora si se asume que cada subintervalo es muy pequeño se puede suponer la fuerza en cada uno de ellos como constante y aproximar el trabajo en cada subintervalo mediante la fórmula 1 tomando cualquier punto xk* en este subintervalo y considerando la fuerza como constante f(xk*), teniendo en cuenta que la distancia se corresponde con el ancho de cada subintervalo x1-x0=△x, el trabajo será igual a:
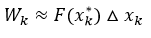
Luego si se suma la aproximación del trabajo realizado en cada subintervalo se puede estimar el trabajo total realizado por la fuerza variable
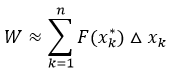
En este punto teniendo en cuenta que mientras menor sea el tamaño de los subintervalos más cercana es la aproximación, si se toma un valor de n que tienda a infinito y se asumen los subintervalos infinitamente pequeños por lo cual la aproximación del trabajo realizado en cada uno de ellos tenderá a ser exacta, es decir:
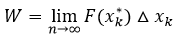
Cuando n tiende a infinito el máximo valor del tamaño de los subintervalos debe aproximarse a cero, es decir
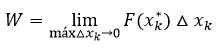
Convenientemente la fórmula anterior es la misma fórmula de la Suma de Riemann en un intervalo la cual se corresponde con el concepto de Integral Definida, es decir, se puede establecer que
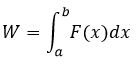
En resumen, se ha llegado al siguiente resultado
Si un objeto se mueve en la dirección positiva a lo largo de un intervalo [a,b], mientras es sometido a una fuerza variable F(x) aplicada en la misma dirección que el movimiento, entonces, el trabajo W efectuado por la fuerza sobre el objeto equivale a
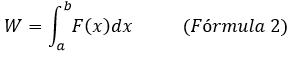
Existen diversos casos en los que la fuerza que actúa sobre un objeto es variable, por ejemplo, la vibración de un resorte actuando sobre un objeto que se desliza bien sea horizontalmente (en una superficie sin fricción) se describe como un movimiento armónico simple en el cual la fuerza es variable, este tema ha sido estudiado desde la perspectiva de la dinámica del movimiento armónico simple en un artículo anterior. En relación la variación de la fuerza en este tipo de movimiento el físico inglés Robert Hooke (1635-1703) estableció una ley que actualmente lleva su nombre, en términos generales la Ley de Elasticidad de Hooke plantea que:
Si un resorte se estira (o se comprime) L unidades respecto de su posición natural, entonces el resorte jala (o empuja) con una fuerza de magnitud
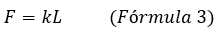
En esta ley k es una constante con valor positivo, la cual se denomina constante del resorte y se mide en unidades de fuerza por longitud, el valor de la constante del resorte depende de diversos factores (grosor del resorte, composición, entre otros).

Resorte en posición de equilibrio. Imagen elaborada por @ydavgonzalez utilizando el editor de imágenes GIMP.
En el artículo anterior se analizó el movimiento armónico simple realizado por el objeto situado en el extremo del resorte, el presente artículo se centra en la determinación del trabajo realizado por el resorte mientras desplaza al objeto de un punto a otro.
Al realizar el análisis del trabajo efectuado en el movimiento del resorte se utilizará la fórmula 2 para el cálculo del trabajo realizado por una fuerza variable en combinación con la ley de elasticidad de Hooke (fórmula 3).
Ejemplo de aplicación:
Un resorte ejerce una fuerza de 50 newtons cuando se estira 10 metros más allá de su punto de equilibrio.
A) Determine la constante del resorte.
B) Calcule el trabajo requerido para estirar el resorte 18 metros más allá de su punto de equilibrio.
Solución: Parte A)
Como el resorte está en su punto de equilibrio antes de ser estirado se puede determinar el valor de la constante del resorte utilizando la ley de Hooke y los datos del problema:
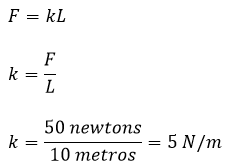
Solución: Parte B)
Si se quiere alargar el resorte x metros se debe aplicar una fuerza equivalente a:
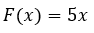
Ahora, debido a que se desea calcular el trabajo requerido para estirar el resorte 18 metros, es decir, alargarlo de 0 a 18 metros (asumiendo el punto de equilibrio como x=0) se cumple que
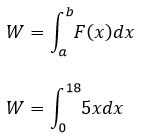
Esta integral definida puede resolverse utilizando el teorema fundamental del cálculo, es decir, encontrando una antiderivada a 5x
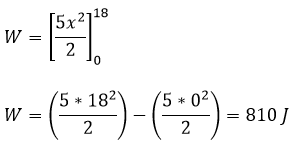
Por lo tanto el trabajo requerido es de 810 joules.
En el ejemplo mostrado anteriormente se resolvió la integral definida aplicando el teorema fundamental del cálculo, es decir, para determinar el valor de la integral definida se procedió a calcular la antiderivada de la función y a evaluarla en los límites de integración. Sin embargo, algunas integrales no pueden ser resueltas por este procedimiento debido a que existen funciones de las cuales no puede encontrarse una antiderivada. Entonces ¿Cómo se resuelven este tipo de integrales?
Resolver una integral definida consiste básicamente en encontrar el valor numérico de dicha integral, lo cual no implica necesariamente resolver la integral indefinida (encontrar una antiderivada de la función), para encontrar el valor numérico en los casos en que no se puede encontrar la antiderivada se utilizan una serie de métodos numéricos, en el problema presentado en este artículo se utilizará la regla de Simpson.
Regla de Simpson
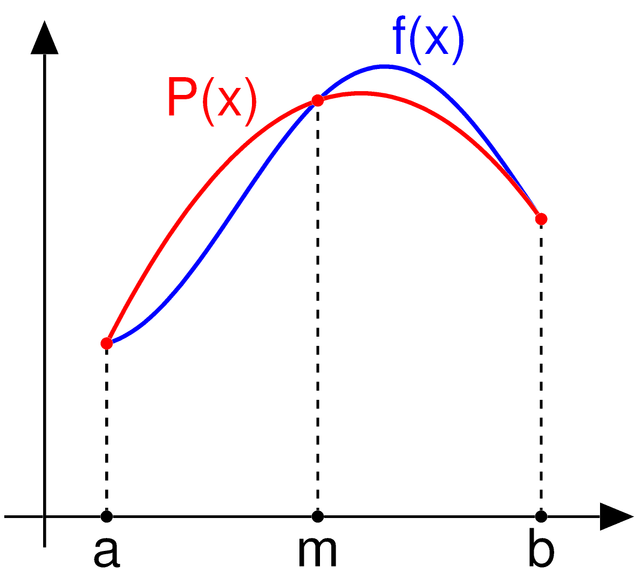
Imagen de Dominio Público Licencia CC0. Autor: Oleg Alexandrov, Año 2005.
Disponible en el siguiente enlace
Entre los métodos numéricos utilizados para resolver integrales definidas uno de los más precisos es la denominada regla de Simpson la cual se basa en aproximar la integral definida mediante áreas de regiones encerradas por parábolas.
De esta forma calculando cada una de estas áreas y realizando la sumatoria de todas ellas se puede aproximar el valor de la integral definida.
Supongamos que se quiere aproximar el valor de la integral definida en [a,b], tomando una partición regular del intervalo [a,b] determinada por los puntos:
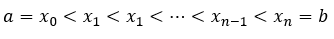
Y sean P0, P1, P2, … Pn-1, Pn puntos correspondientes sobre el gráfico de f(x), con la restricción de que n sea par, se pueden construir una serie de curvas en las cuales P0, P1 y P2 formen una parábola; P2, P3 y P4 formen otra parábola y así sucesivamente.
Ahora bien recordando que la definición de la integral definida corresponde con el área bajo la curva de f(x) en el intervalo [a, b] se puede aproximar su valor utilizando la sumatoria del área de cada una de las parábolas, es decir, mediante el procedimiento que se detalla a continuación.
Asumiendo a n como un número par, si se toma una partición del intervalo [a,b] en la que
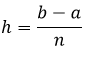
La partición vendrá dada por
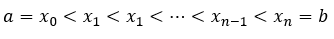
Los puntos en la gráfica según esa partición serian:
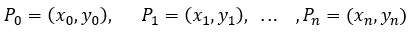
Ahora asumiendo que cada tres de estos puntos forman una parábola (El último punto de cada parábola es el primero de la siguiente), P0, P1 y P2 forman una parábola; P2, P3 y P4 forman otra parábola y así sucesivamente. Se debe determinar el área de cada parábola y luego realizar la sumatoria total.
Con el objetivo de simplificar las operaciones para la primera parábola se asume que x1=0, esto implica que:
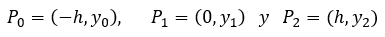
Como la forma general de una parábola se corresponde con una ecuación cuadrática se cumple que viene dada por la función:
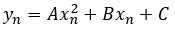
Sustituyendo los valores de los 3 puntos de la primera parábola se cumple que
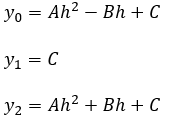
Con lo cual se puede observar que
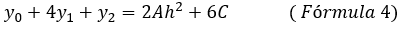
Por definición se sabe que el área de la parábola viene dada por la integral definida evaluada en los extremos del intervalo, es decir
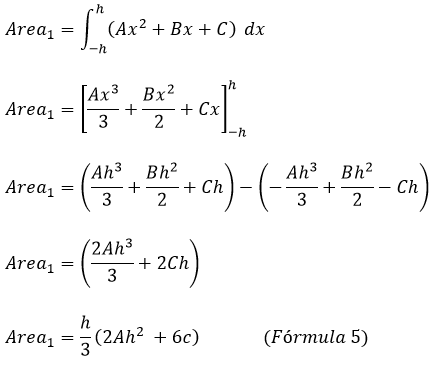
Sustituyendo la fórmula 4 en la fórmula 5 se obtiene:
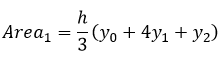
Para la segunda parábola (formada por los puntos P2, P3 y P4) se cumple que
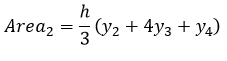
Y en general
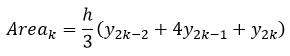
Para calcular el valor de la integral definida se debe realizar la sumatoria de las áreas de cada parábola, obteniendo como resultado
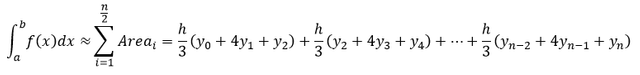
Es decir
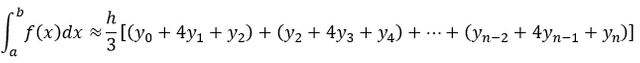
Que puede simplificarse como
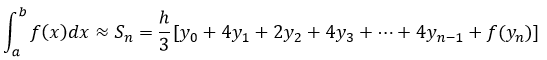
Finalmente teniendo en cuenta que f(xi)=yi y que
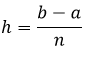
Se llega a la forma general de la Regla de Simpson
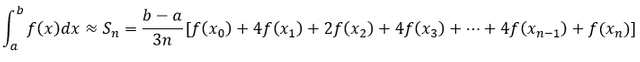
Donde n es un número par.
Observe como cambian los coeficientes:
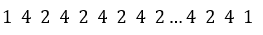
Esta regla permite obtener una aproximación muy precisa al valor de la integral definida sin necesidad de encontrar la antiderivada, ahora se aplicará esta regla al problema de trabajo presentado en este artículo (Fórmula 3).
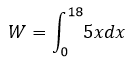
Utilizando n=4 particiones se obtienen los siguientes valores para xi y f(xi)
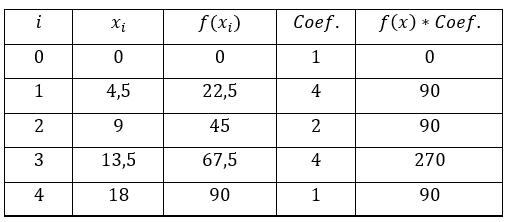
Tabla N° 1 Valores obtenidos al aplicar la regla de Simpson para calcular la integral definida de forma numérica. Fuente: Elaboración propia.
Aplicando la regla de Simpson
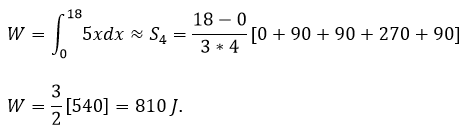
Como se puede apreciar el resultado obtenido utilizando la regla de Simpson coincide exactamente con el que corresponde al aplicar el teorema fundamental del cálculo mediante la integral indefinida, esto pone de relieve la gran precisión de este método numérico, en ambos casos se concluye que se requieren 810 joules para estirar el resorte 18 metros más allá de su punto equilibrio.
Conclusiones y Observaciones
La integración numérica puede ser utilizada como una alternativa a la integración analítica y es la única vía de solución para diversos problemas en los que no se puede encontrar una antiderivada a la función original.
La regla de Simpson tiene una gran precisión sobre todo cuando se aproxima el valor numérico de integrales definidas de funciones polinómicas de bajo grado.
La ley de elasticidad de Hooke permite calcular la fuerza que experimenta un material elástico asumiendo que no interviene la fuerza de fricción ni la resistencia del aire.
En el caso de la ley de elasticidad de Hooke se realizó el análisis del trabajo en base a una función lineal, sin embargo, la variación de la fuerza que realiza el trabajo puede estar expresada en términos de una función no lineal (por ejemplo, una función trigonométrica).
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editoria Limusa Willey.
González (2018), LEY DE HOOKE APLICADA AL MOVIMIENTO ARMÓNICO SIMPLE DE UN RESORTE EN VIBRACIÓN Y SU RESOLUCIÓN MEDIANTE UNA ECUACIÓN DIFERENCIAL ORDINARIA DE SEGUNDO ORDEN. Disponible en el siguiente enlace.
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Saenz (2009), Cálculo Integral con Funciones Trascendentes Tempranas para Ciencias e Ingeniería. 2da edición Editorial Hipotenusa.
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.

Imagen de Dominio Público. Elaborada por @carloserp-2000 y @iamphysical.
No recuerdo haber visto la Regla de Simpson, pero sí la teoría sobre el trabajo, fuerza y energía. Es un buen lugar para aprender cosas nuevas.
Así es en Steemit hay mucho contenido sobre el cual aprender, saludos @azulear.
Hola, me encanto tu articulo, muy interesante... Un gusto, soy nueva en esta plataforma y tu articulo es un de los primeros que veo, te invito a visitar mi perfil alli me presento, saludos
Bienvenida @kkxara12 me alegra que leyeras mi artículo.
Me encanta la pasión que muestras por las matemáticas y los cálculos numéricos. Saludos.
Gracias por el apoyo @elvigia, saludos.
Mi dolor de cabeza jejeje la Regla de Simpson tenía un profesor que le gustaba muchísimo ese metodo y todo la integrales la quería hacer respecto a ese método , excelente post amigo siempre sorprendes con tus publicaciones
Gracias @gerardoalfred es uno de los métodos más eficientes para resolver este tipo de problemas.
Felicidades. Buenos artículos matemáticos, y la coherencia que llevaste entre uno y otro usando el mismo ejemplo. Es de mucha ayuda para nosotros puestp que nos permite ver más allá en el razonamiento. Éxitos.
Gracias, estimada amiga @isgledysduarte.
Me gustó mucho el artículo @ydavgonzalez, en Física I una de las cosas que me parecían curiosas era cuando el profesor nos decía: “muchachos, el trabajo realizado por una persona que carga a otra de forma perpendicular mientras camina es nulo”, supongo que en futuras entregas compartirás este razonamiento visto desde la fundamentación numérica.
Buenos análisis como de costumbre !
Sin lugar a dudas que la regla de Simpson, es una demostración del poder de los métodos numéricos, en la resolución de problemas donde la solución analítica es complicada o simplemente no se puede obtener. El concepto de integral definida es de grandes aplicaciones en la ingeniería, y me gustó la forma como lo adaptaste al concepto de trabajo. Felicidades @ydavgonzalez y muchos éxitos!
Gracias por el apoyo @eliaschess333, saludos.