ONDAS - PARTE 2: PULSO, TREN DE ONDAS, FRENTE DE ONDA, RAYO, DESCRIPCION DE LA PROPAGACION DE UNA ONDA Y ECUACION DE ONDA.
Saludos Steemians. Continuamos con la parte 2 (de 3) de los posts dedicados a las ondas. A diferencia del anterior, en este estará involucrado el inevitable uso de las matemáticas. Se necesita un conocimiento básico del cálculo integro-diferencial.
La parte 1 la pueden conseguir en:
En el presente post:
Definiremos Pulso, Tren de Ondas, Frente de Onda y Rayo.
Estudiaremos cómo se describe la propagación de una onda.
Mostraremos cuál es la ecuación diferencial que describe a un movimiento ondulatorio, es decir, la Ecuación de Onda.
1. PULSO, TREN DE ONDAS, FRENTE DE ONDAS Y RAYO
1.1. PULSO
Estimados Steemians. Es posible producir una Pulso (una Pulsación) que viaje por una cuerda estirada aplicándole un único movimiento lateral en su extremo, como lo muestra la figura 1 y la figura 2a. Cada partícula permanece en reposo hasta que la pulsación llega hasta ella, luego se mueve durante un tiempo corto y posteriormente permanece nuevamente en reposo.
Un Pulso es una perturbación aislada, no periódica, que tiene lugar en un movimiento ondulatorio de algún tipo. |
|---|
1.2. TREN DE ONDAS
Ahora, mis muy estimados Steemians, si se continúa moviendo el extremo de la cuerda en vaiven como lo muestra la figura 2b, se originará un Tren de Ondas que viajará a lo largo de la cuerda. Entonces podemos decir en este momento que:
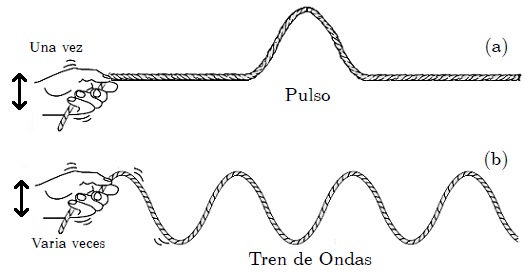
Un Tren de Ondas es una colección de pulsos. |
|---|
Si el movimiento es periódico, entonces se originará un tren de ondas periódico (donde cada partícula de la cuerda tendrá un movimiento periódico). El caso especial más sencillo de una onda periódica es una onda armónica, donde cada partícula experimenta un movimiento armónico simple.
1.3. FRENTE DE ONDA
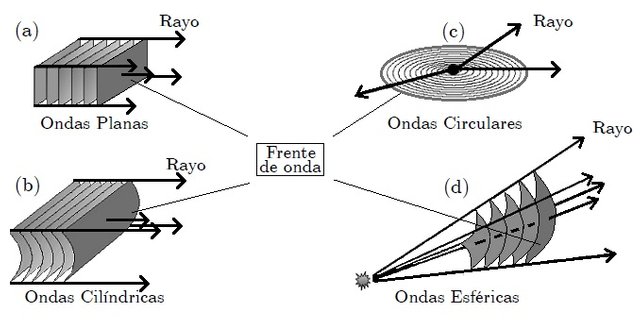
Steemians, imagínense ahora que se lanza una piedra a una piscina tranquila. Ocurrirá que los rizos circulares se esparcen hacia afuera desde el punto en que la piedra entró al agua, como lo muestra la figura 3(c). A lo largo de un rizo circular dado, todos los puntos están en el mismo estado de movimiento. Esos puntos definen una superficie llamada Frente de Onda,
Un Frente de Onda se define como el conjunto de puntos del medio (en el que viaja la onda), alcanzados por el movimiento ondulatorio en el mismo instante. También es posible definirlo como el lugar geométrico que une todos los puntos tal que, en un instante dado, se encuentran en idéntico estado de vibración. |
|---|
1.4. RAYO
Si el medio donde se propagan las ondas es de densidad uniforme, la dirección del movimiento de las ondas está en ángulo recto al frente de la onda y es posible indicar esta dirección mediante los llamados Rayos.
Los Rayos son líneas rectas perpendiculares a los frentes de onda en cada uno de sus puntos que indican, mediante una flecha, la dirección y sentido de propagación de la onda. |
|---|
Pero, estimados Steemians, los frentes de onda pueden tener muchas formas. Una fuente central en la superficie del agua produce ondas bidimensionales con frentes de onda circulares y rayos que salen hacia afuera a partir del punto de la perturbación como en la figura 3c. En cambio, un barra muy larga arrojada horizontalmente al agua originaría (cerca de su centro) perturbaciones que viajan como lineas rectas y cuyos rayos serían líneas paralelas. La analogía tridimensional, en la cual las perturbaciones viajan en una sola direccion, es la onda plana. En un instante dado, las condiciones son las mismas en todas partes de cualquier plano perpendicular a la dirección de propagacion. Los frentes de onda son planos y los rayos son líneas rectas paralelas como lo muestra la figura 3a. La analogía tridimensional de las ondas circulares son las ondas esféricas. Aquí, la perturbación se propaga hacia afuera en todas direcciones desde una fuente puntual de ondas. Los frentes de onda son esferas y los rayos son líneas radiales que salen de la fuente puntual en todas direcciones como lo muestra la figura 3d. Lejos de esta fuente, los frentes de onda esféricos tienen una curvatura muy pequeña y dentro de una región limitada pueden considerarse, a menudo, como planos. Por supuesto, existen otras muchas formas de frentes de onda posibles, entre ellas las cilídricas como lo muestra la figura 3b.
2. DESCRIPCION DE LA PROPAGACION DE UNA ONDA
Supongamos, mis estimados Steemians, que tenemos una cuerda en la cual se hace propagar una perturbación o pulso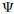 
. Su representación matemática ser una función de la posición y el tiempo, es decir,
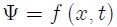
que denominaremos Función de Onda. La forma de la perturbación se obtendrá mediante una "fotografía" o instantánea de la misma. Así, la forma en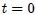 
será 
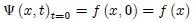. Generalmente su forma variará al moverse.
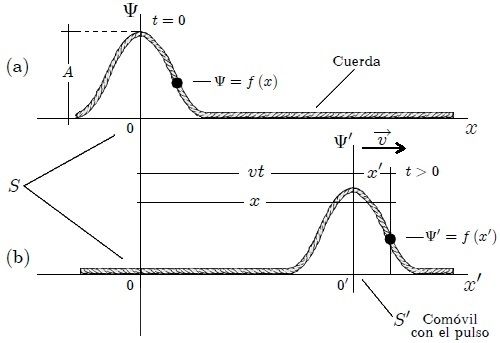
Steemians, como siempre se procede al estudiar algún fenómeno físico, consideremos la posibilidad más simple: que la perturbación se propague, sin variar su forma, mientras avanza hacia la derecha (sentido positivo de las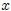 
a velocidad constante 
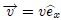. En la figura 4 se muestra un pulso en una cuerda en el instante 
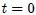en un sistema 
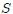inercial (es sistema que puede estar en reposo o en movimiento rectilíneo y uniforme con respecto a otro lo cual, como se sabe, no modifica la física del fenómeno). La forma de la cuerda en este instante puede representarse por una función,
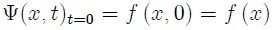
Establezcamos ahora un nuevo sistema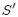 
tal que 
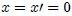en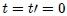 
(es decir, en 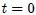ambos orígenes coinciden), que viaje junto con el pulso a velocidad constante 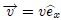(lo cual significa que 
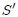es comóvil con el pulso). Por lo tanto, un cierto tiempo después (ver figura 4b), el pulso se habrá desplazado por la cuerda pero permanece estacionario en este nuevo sistema y, para cualquier valor de 
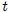en 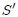, tiene la misma forma que tenía en 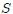para 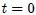(ya que por hipótesis la forma del pulso no varía), por tanto la forma de la cuerda en 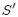vendrá dada por,
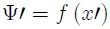
Ahora bien Steemians, de la figura figura 4b es fácil determinar que las coordenadas de los sistemas 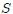y 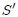están relacionadas mediante,
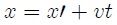
de aquí que,
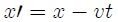
por lo cual, al sustituir este resultado en el argumento de (3), es posible escribir hora que,
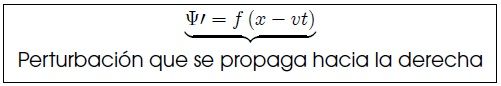
Mediante un razonamiento análogo al anterior es posible determinar que, para una perturbación que se propague hacia la izquierda (sentido negativo de las 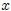) la forma de la cuerda vendrá dada por,
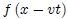que se mueve en sentido 
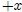y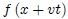 
que se mueve en sentido 
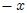(Esta imagen fue elaborada por mi persona @tsoldovieri, usando las aplicaciones PAINT y MAPLE 18).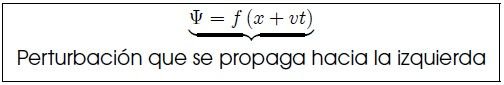
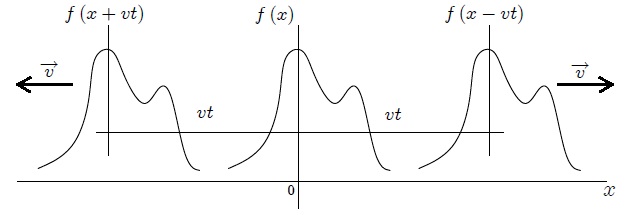
Es posible ahora decir que, independientemente de la forma de la perturbación, las variables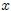 
y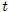 
deben aparecer en la función como una variable simple de la forma 
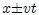. En la figura 5 se muestran los dos casos.
La función (6) puede expresarse también como una función de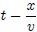 
,
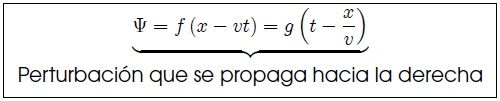
si la forma de la perturbación en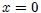 
viene dada por 
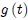, indicando que todo punto 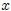sufre la misma perturbación que ha sufrido el origen pero con un retraso de 
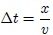. De la misma manera, una onda que se propague en el sentido negativo de las 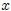se describirá mediante la función,
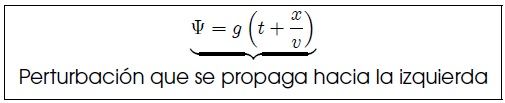
3. ECUACION DE ONDA
Ya a este nivel, estimados Steemians, tenemos los conocimientos básicos para poder profundizar un poco más en el tema de las ondas. Hagámosnos la ahora la siguiente pregunta: ¿cómo se determina la función de onda?. En principio y como es natural que ocurra, la aplicación de las leyes conocidas a algún problema físico da origen a una ecuación diferencial de movimiento (así como ocurrió, en el capítulo anterior, para el caso de los osciladores) cuya solución, para el caso de los problemas aquí abordados, debe conducir a la aparición de una función de onda. Una perturbación ondulatoria u onda puede describirse mediante una función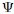 
de la posición y el tiempo, como se vio en las anteriores secciones. Como 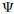es de dos variables entonces la ecuación diferencial de movimiento tiene que ser, para este caso, en derivadas parciales.
Ahora bien, no plantearemos aquí la anterior forma de llegar a la ecuación de onda, sino que el problema se tratará en forma inversa y desde un punto de vista estrictamente matemático: ¿qué tipo de ecuación diferencial en derivadas parciales tiene por solución funciones del tipo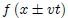 
?. Hay una relación sencilla entre las derivadas parciales respecto a 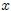y respecto a 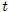de la función 
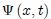. Con la finalidad de encontrar lo anterior, escribamos 
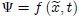de tal forma que 
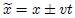(para involucrar ambos sentidos de propagación). Al hacer lo anterior resulta que,
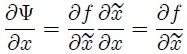
ya que,
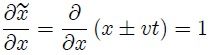
y además,
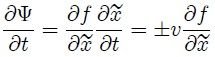
puesto que,
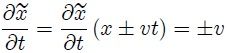
entonces, al sustituir (9) en (11),
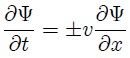
Así pues, para ondas unidimensionales que se propaguen en uno y otro sentido en la dirección 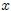, la rapidez de cambio de 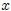con respecto a 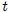y la de 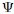con respecto a 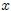son iguales salvo una constante. La ecuación (13) es el primer ejemplo de ecuación de onda. Su solución general 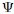representa una perturbación de forma arbitraria, pero que permanece invariable (rígida) propagándose a lo largo del eje 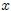con velocidad 
.
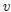Para evitar los signos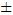 
de la ecuación (13) se toman las segundas derivadas de (9) y (11). De esta manera,
y,
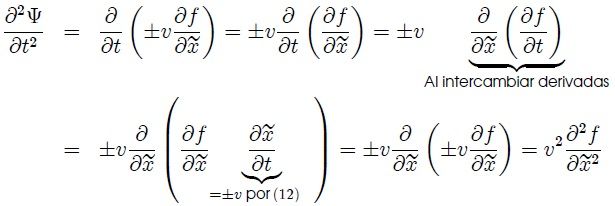
Entonces, al sustituir (14) en (15) resulta finalmente,
Steemians, esta ecuación diferencial recibe el nombre de Ecuación de Onda y la función 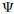recibe el nombre de Función de Onda, como ya se había mencionado antes. Para llegar a la ecuación de onda se ha partido de una onda progresiva y se ha visto que las derivadas respecto 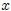a y a 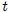guardan esa relación sencilla. De manera inversa, si se sabe que la derivada segunda respecto a 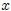de una cantidad 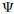es proporcional a la derivada segunda respecto al tiempo 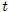de la misma cantidad, entonces 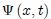es una onda o una superposición de ondas. Además, el cuadrado de la velocidad de propagación debe ser igual al cociente constante entre las segundas derivadas, temporal y espacial.
BIBLIOGRAFIA RECOMENDADA
Soldovieri, Terenzio. FISICA GENERAL - Una introducción a los Fluidos, Vibraciones y Termodinámica. 1era edición (borrador), 2017. Puede descargarse desde mi web http://www.cmc.org.ve/tsweb/
Resnick, R. & Halliday, D. FISICA, volume 1. CIA Editorial Continental, SA de CV, México, 1984.
Serway, R. A. FISICA, volume 1. McGraW-Hill, Mexico, 4ta edition, 1997.
Giancoli, D. C. FISICA GENERAL, volume 1. Prentice-Hall Hispanoamericana, SA, México, 1988.
Alonso, M. & Finn, E. J. FISICA - MECANICA, volume 1. Fondo Educativo Interamericano, S.A., 1970. pp. 21 - 23 51 - 53.
Resnick, R.; Halliday, D. & Krane, K. S. FISICA, volume 1. Grupo Patria Cultural, S. A. de C. V., México, 2000.
Sears, F. W.; Zemansky, M. W.; Young, H. D. & Freedman, R. A. FISICA UNIVERSITARIA CON FISICA MODERNA, volume 1. Pearson Educación de México, S.A. de C.V., México, 11er edition, 2004.
Tipler, P. A. & Mosca, G. FISICA PARA LA CIENCIA Y LA TECNOLOGIA - MECANICA, OSCILACIONES Y ONDAS, TERMODINAMICA, volume 1. Editorial Reverté, S. A., 5ta edition, 2005.
Espero que la anterior información les sea de mucha utilidad. El siguiente post (y último) tratará sobre el Principio de Superposición y Ondas Armónicas.
Hasta mi próximo post. ¡Saludos a todos! 😁.
Si deseas leer más artículos científicos de buena calidad, no pierda el tiempo, visite la etiqueta #steemstem. Es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete al canal de @steemstem. También puedes visitar el blog @steemstem y obtener mas información.
Muy buena tu explicacion sobre las ondas
Gracias @jesusvarela. Saludos!.
Estimado @tsoldovieri este artículo resulta muy didáctico para comprender un fenómeno físico que percibidos a cada instante, porque estamos rodeados de ondas de todos los tipos!
Muchas gracias por tu comentario y apoyo @iamphysical. Muy cierto, estamos rodeados de fenómenos ondulatorios. Gracias nuevamente. Saludos.
Saludos colega. Muy bello tu post. Te espero de visita por mi blog. Saludos
Gracias por su comentario y apoyo mi muy hermosa colega @emily61. Claro, ya me paso por allá. Saludos.
Te felicito @tsoldovieri me hubiese encantado que me dictaras clases de física, porque tus presentaciones son muy didácticas. Abrazos
Gracias @viagaby. Es para mi gratificante que te gusten mis presentaciones. Saludos! 😁
Muy buena explicación y fácil de aprender. Saludos.
Gracias amiga @maeugenia. Saludos.
Hermano perijanero @tsoldovieri, gracias por compartir de forma didáctica y amena los principios relacionados con las ondas. ¡Saludos!
Gracias por tu comentario y apoyo mi perijanero hermano @hugobohor. Trataré siempre de hacerlos así. Saludos.