Continuando con la temática química, en esta oportunidad relacionada al ajuste o igualación de reacciones químicas por medio de sistemas equivalentes triangulares utilizando el método de Gauss en forma matricial, antes de entrar en el desarrollo de dicho ajuste, necesario es, realizar un breve repaso sobre sistemas de ecuaciones lineales, recordar una ecuación lineal, identificar también los sistemas de ecuaciones lineales 2x2 y 3x3, es decir, sistemas con dos y tres ecuaciones y/o incógnitas respectivamente, así como algunos métodos utilizados para solucionarlos, de igual manera sistemas con elevados números tanto de ecuaciones como de incógnitas, las formas de los sistemas triangulares tanto inferior como superior en notación matricial, los métodos utilizados para llegar a este tipo de sistemas triangulares.

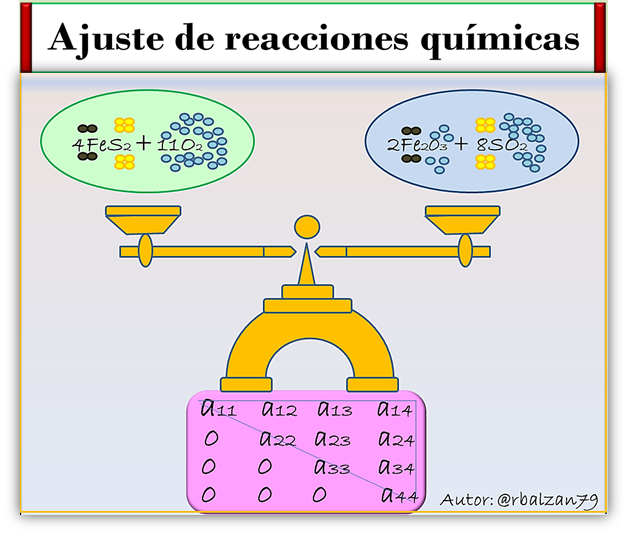
También recordar o conocer algunos conceptos importantes sobre las reacciones químicas como los átomos y moléculas los cuales son los elementos y compuestos que intervienen en dichas reacciones, las mismas requieren de un ajuste o balance adecuado de su ecuación para un óptimo resultado en cuanto a la composición de los productos finales, todo esto nos permitirá calibrar adecuadamente nuestra herramienta algebraica de notación matricial, partiendo siempre del principio elemental para las resoluciones de problemas complejos en cualquier ámbito, iniciar desde lo más simple para consolidar las soluciones para lo más complejo, por lo tanto, podemos iniciar nuestro interesante recorrido recordando lo siguiente:

Por lo tanto, podemos decir que un sistema de ecuaciones lineales está representado por un conjunto de ecuaciones las cuales comparten las mismas incógnitas, es importante tener muy claro algunos fundamentos esenciales tales como despejar una incógnita, saber reconocer una expresión de primer grado, así como recordar que una ecuación no es más que una igualdad la cual solo se cumple para un determinado valor el cual satisface dicha igualdad, por lo tanto, estas igualdades que se cumplen siempre representaran identidades.

Cuando estamos en presencia de un determinado sistema de dos ecuaciones de primer grado con dos incógnitas, para resolverlo tenemos que hallar dos números, debido a que tenemos dos condiciones independientes (incógnitas), las cuales dichos números deben cumplir, de esta misma forma ocurre al tener que resolver un sistema de tres ecuaciones con tres incógnitas y así sucesivamente, lo que generalmente puede variar serán los métodos a utilizar y este será uno de nuestros principales objetivos en esta publicación, poder identificar algunos de estos importantes métodos, y aplicarlos a las reacciones químicas para lograr su ajuste atómico.

Por ahora vamos a describir los distintos métodos que podemos utilizar para solucionar un sistema de ecuaciones lineales 2x2, los mismos son:

Sustitución:

Este práctico método consiste en despejar una incógnita de una de las ecuaciones que conforma dicho sistema, para después sustituir el valor en la otra ecuación, luego procedemos a desarrollar las operaciones pertinentes, convirtiendo esta ecuación en una expresión de primer grado pero ahora con una sola incógnita, por ejemplo:

Despejada la variable procedemos al siguiente paso el cual consiste en sustituir este valor de (y) en la otra ecuación, es decir, en la ecuación 2.

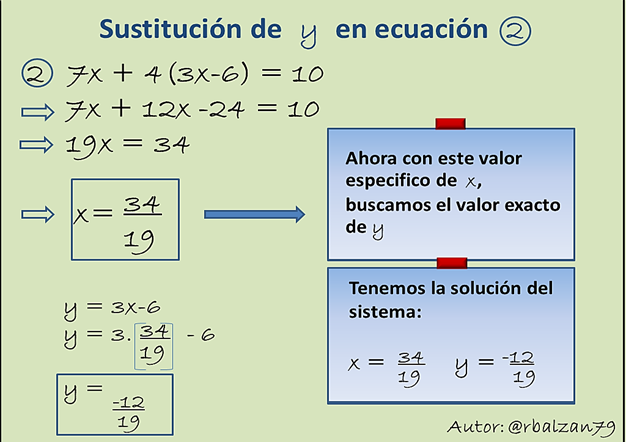
Entonces solo nos queda comprobar sustituyendo los dos valores encontrados en cada una de las ecuaciones del sistema para poder ver si se cumplen las igualdades respectivas:

Igualación:

Este método algebraico consiste en despejar una de las variables de las ecuaciones que conforman el sistema, donde la incógnita a despejar debe ser la misma en ambas ecuaciones, por ejemplo:

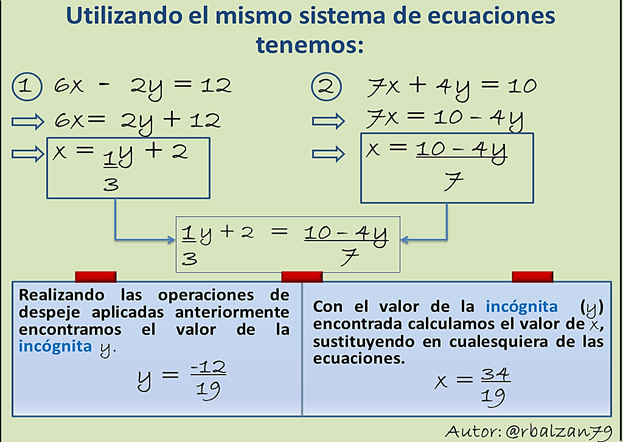
La comprobación la realizamos en el método anterior, solo utilizamos otro tipo de método el cual nos permitió obtener los mismos resultados, por lo tanto, comprobamos que el método algebraico a utilizar para resolver un determinado sistema de ecuaciones no influye en la solución.

Método de Reducción:

Este método consiste en multiplicar algún miembro de cada ecuación por un determinado número conveniente, todo esto con la firme finalidad de que las incógnitas tengan coeficientes iguales pero con signos diferentes en las dos ecuaciones relacionadas, de esta manera obtendremos una ecuación con una sola incógnita. Por ejemplo:

La comprobación será igual que las realizadas con los otros métodos, lo que podemos resaltar nuevamente es que hemos comprobado que sea cual sea el método que seleccionemos, el resultado o solución será siempre el mismo.

Es importante resaltar los tipos de soluciones que podemos tener de un determinado sistemas de ecuaciones de primer grado, ya que puede llegar a tener una única solución, por lo tanto, diremos que estamos en presencia de un sistema compatible determinado como el que acabamos de resolver; pero también puede ocurrir que no tenga ninguna solución, y le daremos el nombre de sistema incompatible, pero también podemos estar en presencia de un sistema con infinitas soluciones, al que denominaremos sistema compatible indeterminado.

Sistemas de ecuaciones 3x3:

Ahora tenemos un sistema de tres ecuaciones con tres incógnitas, para solucionar el mismo estaremos implementando el método de sustitución, ya que despejaremos una de las incógnitas de cualesquiera de las ecuaciones presente en dicho sistema, para luego sustituir la expresión que hemos obtenido en las otras dos ecuaciones, por lo tanto, vamos a obtener dos ecuaciones con las incógnitas restantes, es decir, un nuevo sistema que para este caso quedará de 2x2, dos ecuaciones y dos incógnitas, y este tipo de ecuaciones ya lo sabemos resolver, aplicando cualquier método algebraico antes desarrollado se obtendrán dos soluciones ( si las tiene), para luego sustituir en la ecuación conseguida mediante el despeje de una de sus variables, conseguiremos el valor de la incógnita eliminada inicialmente, por ejemplo:

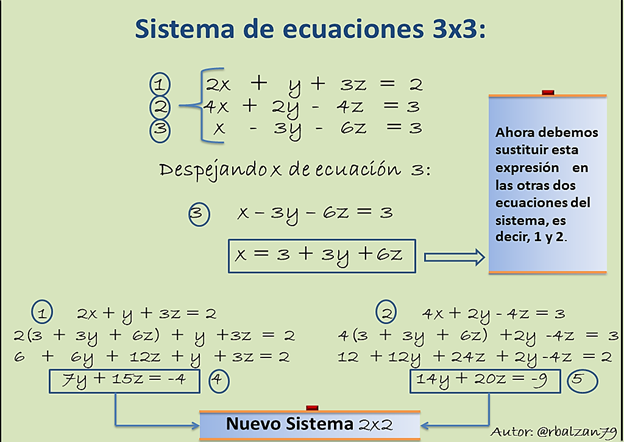
Observamos que al efectuar las operaciones correspondientes, obtenemos nuestro nuevo sistema ahora formado por las ecuaciones 4 y 5, los cuales son de dos incógnitas, y como hemos desarrollado este tipo de sistema es posible realizarlo a través de los métodos ya estudiados (sustitución, igualación y reducción). Pueden escoger el método de su preferencia para este caso escogeremos el de reducción:

Los métodos antes desarrollados podemos aplicarlos generalmente en sistemas lineales que cuentan con pocas ecuaciones e incógnitas, por lo tanto, es importante conocer la aplicación de otros métodos los cuales nos permitan resolver sistemas de ecuaciones lineales muchos más complejos, es decir, con un número elevado tanto de ecuaciones como de incógnitas, entonces, nos basaremos en conocer métodos más adecuados para poder resolver estos tipos de sistemas con mayor grado de dificultad, estos métodos son los que logran la construcción de un sistema equivalente al sistema lineal dado, en pocas palabras con la misma solución, el objetivo principal que sea mucho más fácil de resolver, en resumidas palabras la conformación de sistemas triangulares, tanto superior como inferior, debido a su práctica estructura escalonada, es posible darnos cuenta que podemos calcular dichas incógnitas una a una, iniciando de arriba abajo o de abajo hacia arriba según sea el caso del sistema que deseamos conformar, en nuestro caso estudiaremos o aplicaremos los sistemas triangulares superiores en notación matricial, primeramente conoceremos estos sistemas triangulares para luego ubicar el método que nos permita llegar a estos tipos de sistemas, que para nuestro caso sería en notación matricial.

Sistemas triangulares:

Poder estructurar cualquier sistema de ecuaciones en uno equivalente triangular (si es posible) bien sea inferior o superior dicho sistema será más fácil de resolver, debido a que cada una de las incógnitas las vamos despejando de una en una para ir sustituyéndolas en las otras ecuaciones, por ejemplo:

Sistema triangular inferior:

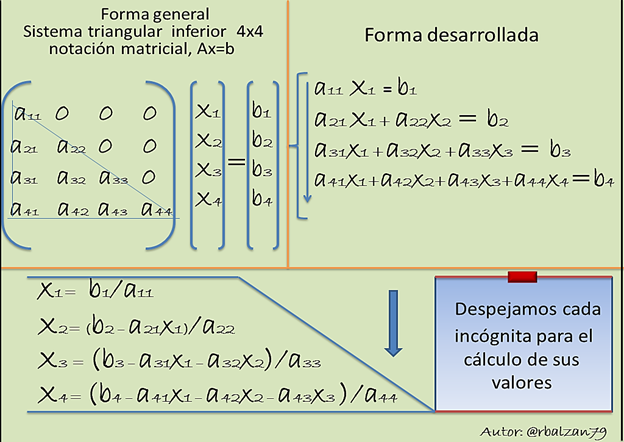
El procedimiento llevado a cabo la denominamos algoritmo de bajada, debido a que las incógnitas la vamos buscando por recurrencia, para este caso de arriba hacia abajo, esta estructura la podemos encontrar en cualquier sistema de elevado número tanto de ecuaciones como de incógnitas, pero el inconveniente se presenta cuando tengamos que llevar dicho sistema a la forma triangular ya que el mismo no posea está determinada estructura, ese es el objetivo de esta publicación, poder encontrar los métodos siempre y cuando el sistema permita convertirlo en triangular inferior o superior, para nuestro caso particular aplicaremos la estructura triangular superior.

Sistema triangular superior:

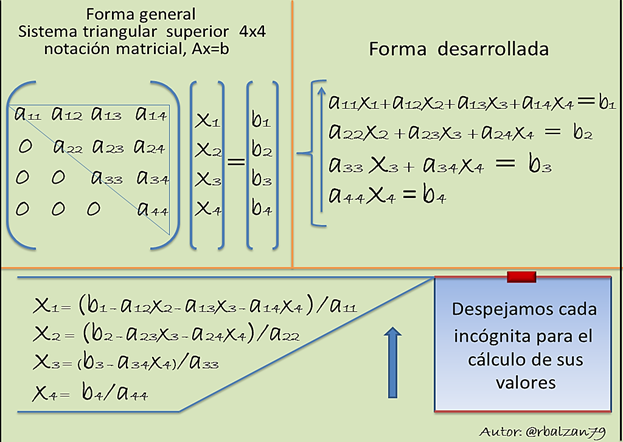
En este procedimiento llevado a cabo la denominamos algoritmo de subida, debido a que las incógnitas la vamos buscando por recurrencia, para este caso sería entonces de abajo hacia arriba.

Con estos sistemas triangulares (superior e inferior), podemos llegar a la estructuración de nuestros sistemas equivalente, con la principal finalidad de poderlo solucionar lo más práctico y fácil posible.

Sistemas equivalentes:

Podemos decir que dos sistemas pueden considerarse equivalente si ambos tienen las mismas soluciones, por lo tanto, ciertas operaciones o propiedades nos permiten poder transformar un determinado sistema en otro equivalente, para ello debemos considerar lo siguiente:

1.- Podemos cambiar el orden de las ecuaciones de un determinado sistema dado.

2.- También podemos multiplicar dos miembros de una de las ecuaciones lineales por el mismo número el cual debe ser distinto de cero.

3.- Podemos eliminar una determinada ecuación de nuestro sistema, la cual veamos que sea combinación lineal de las otras.

4.- Dentro del mismo sistema podemos cambiar una de las ecuaciones por una combinación lineal de sí misma, así como de algunas de las otras.

Tenemos entonces identificadas las propiedades para poder transformar un determinado sistema lineal en otro equivalente pero con mayor facilidad de resolución, pero es importante resaltar la vía o el método a utilizar para llegar a tal propósito, es decir, convertir al sistema lineal en uno equivalente de forma triangular superior que es nuestro propósito, por lo tanto, el reconocido método de Gauss nos permite obtener el objetivo antes planteado haciendo uso de las propiedades mencionadas anteriormente para la obtención de sistemas equivalentes de forma triangular superior el cual lo aplicaremos en notación matricial para el ajuste de reacciones químicas.

Método de Gauss:

Este método consiste en procedimientos sucesivos tales como:

• Vamos a tener una serie de etapas las cuales nos van a permitir llegar a nuestro objetivo, por lo tanto, en cada una de las etapas, debemos tratar de sustituir por cero cada coeficiente que se encuentra por debajo de la diagonal del sistema.

• Al realizar lo antes planteado, es decir, las transformaciones elementales, vamos sustituyendo cada ecuación correspondiente del sistema por otra la cual haga a dicho sistema equivalente y que a su vez tenga nulos tales coeficientes por debajo de la diagonal principal.

• De esta manera llegaremos a nuestro sistema triangular equivalente, el cual, lo resolveremos mediante el algoritmo de subida.

Es importante hacer referencia sobre las transformaciones de este método, las cuales se llevan a cabo directamente sobre cada ecuación del sistema, pero es posible hacer dichas transformaciones de manera más práctica en notación matricial del determinado sistema, que es nuestro caso estudiarlo desde ese punto de vista, por lo tanto, debemos proceder de la siguiente manera:

1.- Debemos escribir nuestro sistema en forma matricial, es decir, Ax = b, en donde A es la matriz, la literal x será el vector de nuestras incógnitas y por ultimo b será el vector de los términos independientes de dicho sistema.

2.- Construimos la matriz ampliada que corresponda, la cual será una matriz que denotaremos [AIb], la misma la formamos con la inclusión del vector b que será la última columna de la matriz A.

3.- Debemos aplicar todas las operaciones elementales que nos permita construir la matriz triangular superior.

Ya calibrado el método algebraico en notación o forma matricial, la cual utilizaremos para nuestro ajuste en reacciones químicas, nos introducimos entonces al breve recorrido en el área de la química, específicamente en sus reacciones, para conocer algunos conceptos importantes dentro de esta área, por lo tanto, tenemos:

Átomo:

Este representa la unidad más pequeña o de menor cantidad de un determinado elemento químico el cual posee existencia propia y que a su vez puede entrar en combinación, destacando que está compuesto por un núcleo de protones y neutrones con una cubierta de electrones, el átomo se mantiene eléctricamente neutro, debido a que el número de protones de su núcleo es igual al número de electrones presentes en la corteza del mismo, por lo tanto, llamamos número atómico a la cantidad de protones que se encuentran presente en un determinado núcleo de un átomo que forma parte de un elemento.

Un determinado átomo puede ganar o perder uno o más electrones, convirtiéndose su carga en positiva o negativa, dando origen a la aparición de un ion, estos iones son los que denominamos cationes si su carga es positiva y si su carga es negativa lo denominamos aniones.

Molécula:

Está constituida por una determinada agrupación de dos o más átomos los cuales se encuentra unidos mediante enlaces químicos, la molécula representa para una sustancia lo que el átomo representa para un elemento cualesquiera, es decir, una molécula es la mínima cantidad presente en una determinada sustancia la cual tenga la capacidad de existir en estado libre, conservando además todas sus propiedades químicas, Las moléculas presentes en los elementos ( sustancia la cual no es posible dividirlas en otras más simple por medios químicos) están constituidas por uno o más átomos idénticos, es decir, de la misma clase, pero las moléculas presentes en los compuestos químicos están constituidas por al menos dos átomos de diferente clase.

La materia la cual constituye o da origen a cualquier cosa o entidad de nuestro entorno la podemos encontrar en dos distintas formas, homogénea y heterogénea, dependerá de sus propiedades y composición, sean iguales en cualquier punto (homogeneidad) o que las mismas cambien al pasar de un punto a otro (heterogeneidad).

Compuestos químicos:

Cuando hablamos de compuestos químicos nos estamos refiriendo a sustancias puras (fase homogénea de composición constante), formados por más de un tipo de átomos, estos compuesto generalmente los podemos descomponer, por medio de la acción de la corriente eléctrica (Electrolisis), por medio de la acción del calor y por supuesto por medios químicos, resaltando que en ninguno de los casos por medios físicos únicamente, también existen sustancias puras que no es posible descomponerlas, las mismas están representadas por los elementos químicos que están presentes en nuestra naturaleza, existen algunos elementos con características artificiales inestables, como sabemos estos elementos se dividen o clasifican en metales; aluminio(Al), hierro(Fe ), cobre(Cu), níquel(Ni), plata(Ag) entre otros, y no metales; hidrogeno(H), flúor(F), cloro(Cl), iodo(I), oxigeno(O) entre otros, quedando algunos pocos con características de intermedios conocidos como semimetales o metaloides; arsénicu(As), teluriu(Te), antimoniu(Sb), entre otros.

Reacción Química:

Cuando estamos en presencia de nuevas sustancias a partir de la transformación de una o más sustancias decimos que este proceso es denominado reacción química, en las que las sustancias iniciales se llaman reactivos, y las que se obtienen las denominamos productos de la reacción, cuya formulación general es la siguiente:

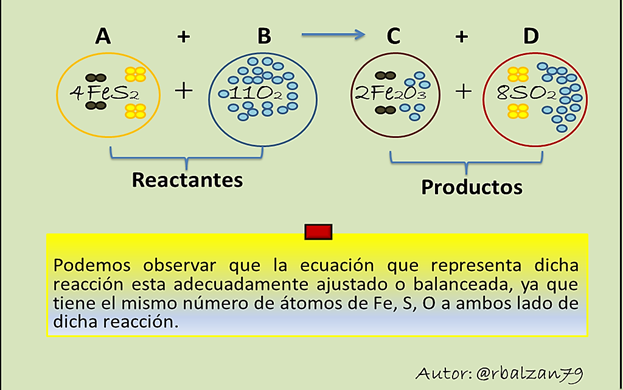
Recordando que A y B, son las sustancias reaccionantes, C y D representan los productos de la reacción. Anexo enlace de mi publicación anterior. Química así de natural.

Como ya hemos expresado en las reacciones químicas se relacionan diferentes tipos de elementos como compuestos dando origen a otros nuevos de composición distintas, esta relación debe llevar una adecuada proporción a ambos lados de dicha reacción, por lo tanto, estas reacciones la representamos a través de ecuaciones las cuales nos informan de todas las condiciones en que ocurre un determinado cambio químico, entonces, para poder tener el éxito requerido necesitamos ajustar, igualar o balancear toda ecuación que representa cualquier reacción química.

Tipos de reacciones químicas:

Podemos decir, que la inmensa mayoría de las reacciones químicas pertenecen a los siguientes tipos de reacciones:

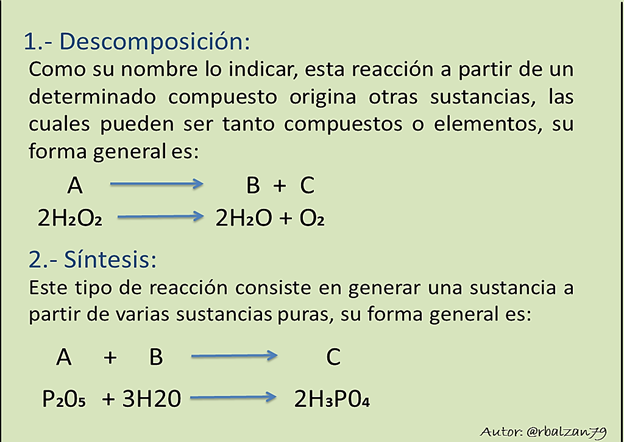
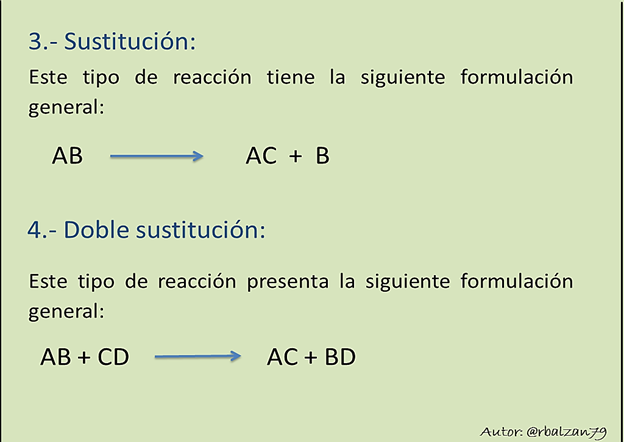
Ahora podemos proceder a realizar el ajuste de una reacción química, recordando que en proporciones adecuadas un conjunto de sustancias las que llamamos reactivos se convierten o transforman en otras diferentes que denominamos productos, estas reacciones deben de estar ajustadas, tanto las sustancias reactantes como las que se originan de ellas, generalmente estas cantidades vienen expresadas en números enteros.

Procedemos ajustar los coeficientes (a, b, c, d, e, f) de la siguiente reacción química mediante la aplicación de un sistema equivalente de forma triangular superior constituido mediante el método de Gauss en notación matricial:

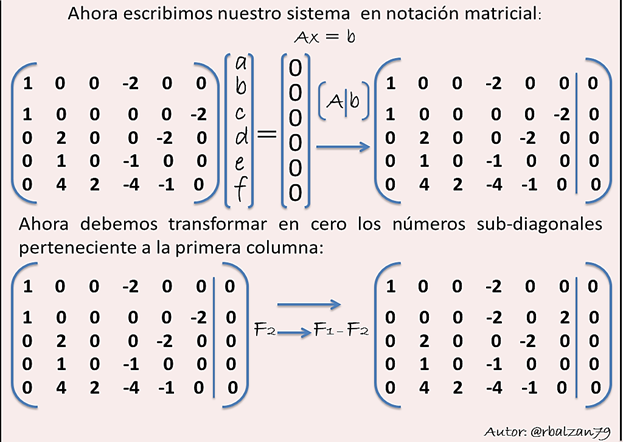
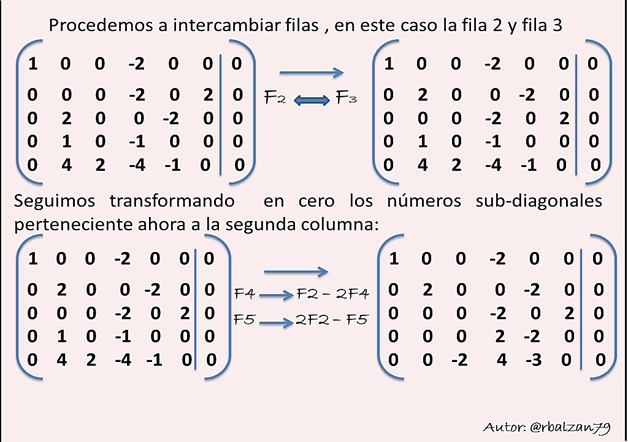
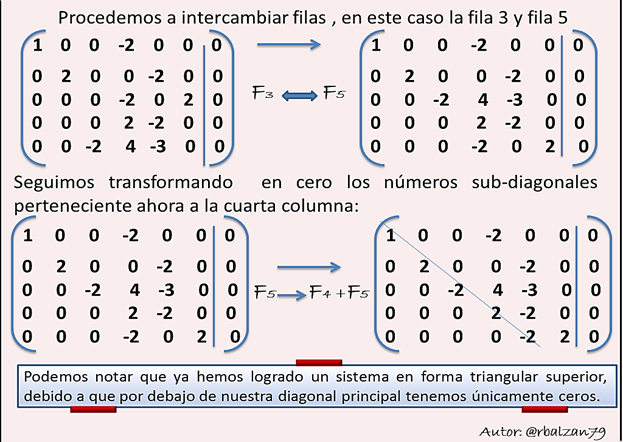
Ahora procedemos a verificar si los valores de cada uno de los coeficientes encontrados nos permiten ajustar o balancear la ecuación de nuestra reacción química planteada, procedamos:

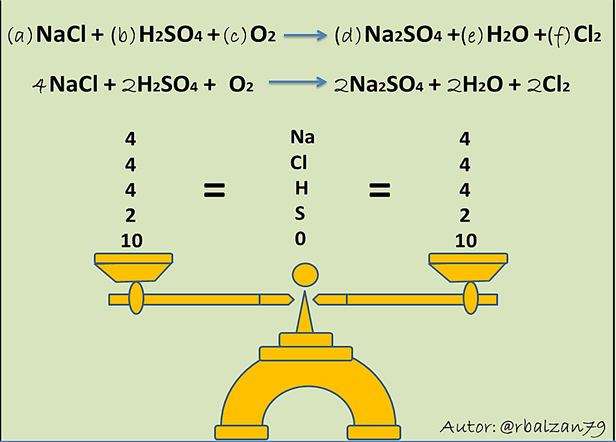
En conclusión, podemos decir, que la ecuación de la reacción química planteada esta adecuadamente en equilibrio, es decir, ajustada o igualada, a través de un sistema equivalente de forma triangular superior mediante la aplicación del método de Gauss en notación matricial, una herramienta muy útil para reforzar gratamente a los métodos ya existente en esta área como los son; método por tanteo, Aritmético y método redox.

Comprobamos además que la química es una ciencia con fuertes lazos de hermandad con numerosas ramas científicas, en este caso una sub-rama de las matemáticas, el álgebra, el lenguaje abstracto por excelencia, por lo tanto, más universal y general con la que cuenta la humanidad en todos sus aspectos.

Agradeciendo de ante mano por su acompañamiento en este placentero y nutrido recorrido, hasta la próxima publicación amigos de steemit.com

Nota: Todas las imágenes fueron elaboradas en paint y PowerPoint 2010 para Windows7.

Referencias Bibliográficas Consultadas:

• Raymond Chang, Williams College. Química. Séptima Edición. Editorial McGrawHill. México, 2002.

• Morrison y Boyd. Química Orgánica. Quinta edición. Versión en español. Addison Wesley Longman de México S.A. 1998.

• Stanley I. Grossman( 1983) . Álgebra Lineal. Grupo Editorial Iberoamérica.

• A. Baldor, Álgebra. Edición 1992. Editora y distribuidora de textos americanos, copyright compañía cultural .

• Universidad de Sevilla. Departamento de Ecuaciones diferenciales y Análisis Numérico. Curso Año 2015-2016.

Autor: @rbalzan79