En primer lugar mis saludos respetuosos para toda la comunidad de #stem-espanol, #steemstem, #utopian-io y #proconocimiento, así como para el resto de la prestigiosa comunidad de steemit, continuando con la temática geometría analítica plana, en donde hemos dado importantes pasos para la comprensión analítica de las matemáticas, así como la utilización de esta características en innumerables áreas tanto académicas como profesionales, en esta oportunidad desarrollaremos inicialmente como en las pasadas publicaciones el aspecto conceptual de los puntos a estudiar para luego poder tener las bases teóricas necesarias para aplicarlas en la resolución de planteamiento o problemas de dichos puntos, los cuales serán los siguientes:

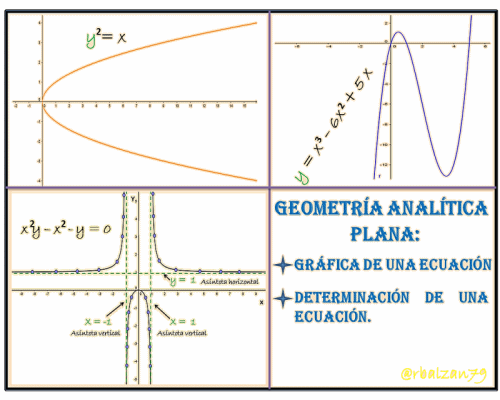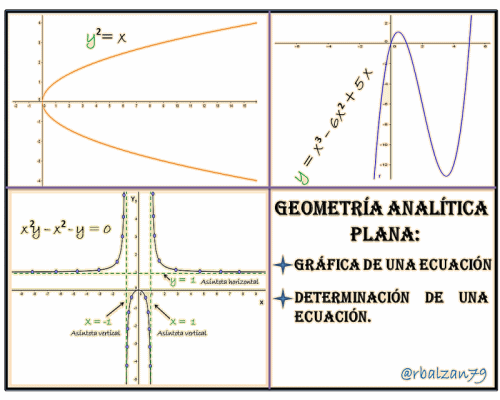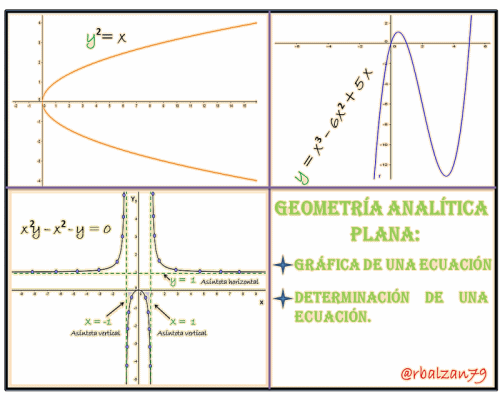
1.- Gráfica de una ecuación

En donde estudiaremos su ecuación mediante los siguientes puntos:

• Intercepción con los ejes.
• Simetría con los ejes y el origen en el plano.
• Extensión de una curva.
• Asíntotas.
• Construcción de curvas.

2.- Determinación de la ecuación de una gráfica o lugar geométrico

Introducción

Todo sabemos la importancia de poder comprender a través de una ecuación o expresión algebraica la conformación e interpretación de una determinada gráfica pero igualmente de la condición inversa donde mediante una figura geométrica o por medio del conocimiento de las condiciones que deban cumplir los puntos que las conforman, podamos determinar su ecuación. De esta manera enfocamos los dos principales planteamientos o problemas fundamentales de la geometría analítica en su versión plana, la cual a través de tales planteamientos seguiremos dándoles características de comportamiento analítico a las matemáticas en general.

Iniciemos con el desarrollo conceptual de los referidos puntos a tratar, por lo tanto, analizaremos el primer planteamiento:

Gráfica de una ecuación

Como seguimos con el comportamiento de figuras geométricas en el plano, debemos suponer que tenemos una ecuación dada de dos variables, es decir, (x , y) las cuales podemos representarla de la siguiente manera:

En términos generales sabemos que podemos encontrar una cantidad infinita de valores para este par de variables y que dichos valores satisfacen la ecuación dada, ya sabemos que en un plano cada par de números reales lo tomaremos como las coordenadas (x , y) de un determinado punto en dicho plano. Entonces podemos apoyarnos en esta importante característica para expresar que cuando un determinado conjunto de puntos, y únicamente aquellos puntos donde sus coordenadas puedan satisfacer la ecuación dada (1), entonces de esta manera a este conjunto de punto se les denomina la gráfica de la ecuación o también la representación de su lugar geométrico que para este caso será en el plano, por lo que también podemos expresar que cualquier punto donde sus coordenadas satisfagan dicha ecuación dada (1) pertenecerá a la gráfica de dicha ecuación. Debido a que cada una de las coordenadas de los puntos los cuales representan un determinado lugar geométrico o gráfica están restringidos por su ecuación, entonces, dichos puntos estarán localizados o ubicados, en términos generales podemos tomarlos en conjunto, es decir, en un trazo definido el cual podemos denominar curva, gráfica o bien su lugar geométrico.

Hasta ahora habíamos estudiado el lugar geométrico de un punto tanto en un sistema unidimensional como en uno bidimensional, pero también el lugar geométrico de una línea recta a través del estudio de la distancia entre dos puntos dados o también a través de una función afín en el plano del tipo y=mx+b, pasos importantes antes de poder llegar a este planteamiento de la representación gráfica de una ecuación de dos variables.

En las matemáticas la representación gráfica de una determinada ecuación es muy común, sin embargo, la geometría analítica en general para este caso en el plano, es la que ofrece mayor capacidad de análisis a una ecuación para tener mayor precisión en la conformación gráfica de dicha ecuación, los estudiantes requieren de una serie de herramientas para poder lograr el mejor entendimiento al momento de poder plasmar o trazar una determinada ecuación en términos gráficos, esto es debido a que el comportamiento lineal de la curva no es la misma para todo tipo de ecuación, es aquí en donde la geometría analítica desde la visión plana nos ofrece una mayor profundidad al estudio de una determinada ecuación antes del proceso del trazado de su curva, ya que mediante un análisis más profundo de dicha ecuación tendremos mejor dominio al momento de poder determinar su lugar geométrico.

Entonces para iniciar con el estudio en profundidad de una determinada ecuación debemos tomar en cuenta lo siguiente:

1.- Intercepción con los ejes

Es muy importante poder iniciar el análisis de una determinada ecuación con la intercepción de su curva con cada uno de los ejes de coordenadas del plano, ya que cuando esto sucede tendremos que el valor de una de las coordenadas será igual a cero (0) esto dependerá del eje que se intercepte, por lo tanto, si tenemos la intercepción de una curva con el eje de las X esto estará representado por la abscisa del punto de intercepción de dicha curva con el referido eje X, pero de la misma forma podemos definir la intercepción con el eje Y, la cual representa la ordenada del punto de intercepción de dicha curva con tal eje, en palabras más practicas podemos decir, como tenemos la intercepción con el eje de las X esto es la abscisa de un punto que esta sobre dicho eje, y que por lo tanto, la ordenada de dicho punto será igual a cero, esto nos lleva a manifestar para este caso, que cuando hacemos y=0 en la ecuación de la curva analizada vamos a obtener las soluciones reales de dicha ecuación resultante en términos de X, dándonos así las intercepciones con el eje de las X, esto podemos utilizarlo para el caso cuando el punto de intercepción se encuentre sobre el eje Y, y en donde x=0 , obtendríamos las soluciones reales de dicha ecuación en términos de Y dándonos así las intercepciones con el eje ante descrito, es decir, Y.

Ahora mostramos la representación gráfica de dicha ecuación o expresión algebraica de tipo polinómica, con la ayuda de la aplicación de GeoGebra 5.0, en donde podemos observar las intercepciones con cada uno de los ejes coordenado del plano:

2.- Simetría con los ejes y el origen en el plano

Luego de analizar la intercepción de la curva de una determinada ecuación con los ejes coordenados en el plano, ahora estudiaremos el comportamiento de simetría de dicha curva con respecto a los ejes coordenados en el plano, así como con el origen de dicho sistema bidimensional.

Por lo tanto, podemos decir, que dos puntos los cuales conforman un segmento serán simétricos con relación a una línea recta si dicha recta es perpendicular a dicho segmento que los une en su punto medio, llamaremos entonces eje de simetría a la recta perpendicular al segmento entre los dos puntos ahora simétricos por dicho eje.

Entonces podríamos establecer que dos puntos son simétricos a un determinado punto T si T representa el punto medio del segmento que los une, por lo tanto, dicho punto T lo llamaremos centro de simetría, con esto logramos establecer las bases necesarias para poder extenderlas hacia la aplicación de una curva en el plano con respecto a una línea recta o punto.

Por lo tanto, podemos expresar que una curva cualesquiera es simétrica con respecto a un eje de simetría cuando cada uno de los puntos de esta curva tiene un punto correspondiente, también en dicha curva, entonces, estos dos puntos serán simétricos con respecto al eje de simetría, también podemos decir, que una curva será simétrica en relación a un centro de simetría O cuando a cada punto de dicha curva tenga un punto correspondiente también de la misma curva, en donde estos dos puntos serán simétricos en relación al origen (O). Hasta ahora hemos podido realizar una conceptualización desde el punto de vista de la geometría elemental, ya hemos conocido y conformado analíticamente un sistema bidimensional estructurado por dos ejes coordenados perpendiculares entre sí, por lo que podemos utilizarlos como ejes de simetría y cuyo origen (O) de dicho sistema como centro de simetría, con esto le inyectaremos características analítica a las definiciones de simetría antes descritas ahora en el plano.

a.-) Simetría con respecto al eje X

Si tenemos un punto cualesquiera T (x,y) de una determinada curva, esta curva es simétrica en relación al eje de las X, si existe otro punto T´(a , b) sobre dicha curva, tal que origine el segmento TT´ el cual quedará perpendicularmente bisecado por el eje X, en donde un punto al cual llamaremos N por colocarle una literal (puede ser cualquiera de su preferencia), represente el punto medio de dicho segmento TT´, por lo tanto, las coordenadas de este punto N claramente serán (x , 0),ejemplo:

Por lo tanto, mediante la fórmula del punto medio tenemos:

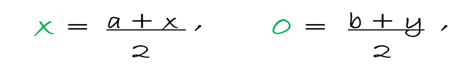
Para esto a = x y b = -y, esto hace que las coordenadas del punto T´ sean ( x , -y), recordemos que todo punto que se encuentre sobre la curva sus coordenadas deben satisfacer a la ecuación de dicha curva, por lo tanto, debido a que T´ se encuentra sobre la curva sus coordenadas deben satisfacer la ecuación de la curva o gráfica que lo contiene, en resumidas palabras, las coordenadas del punto T (x , y) que satisface a la ecuación f (x , y) = 0, también las coordenadas del punto T´(x , -y) deben satisfacer dicha ecuación siempre y cuando la gráfica o curva sea simétrica con relación al eje de las X, es decir, si tenemos que una ecuación de una gráfica o curva no experimenta cambio cuando reemplazamos la variable (y) por (–y), entonces tendremos que dicha curva será simétrica con respecto al eje X. Por ejemplo, si queremos buscar la simetría de la siguiente ecuación con el eje X:

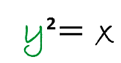
Tenemos que sustituir y por –y, para observar si dicha ecuación experimenta cambio:

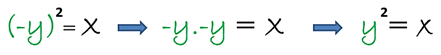
Por lo tanto, al no experimentar cambio la ecuación de dicha curva, la misma es simétrica al eje X, a continuación la gráfica de dicha ecuación con la ayuda de la aplicación GeoGebra 5.0:

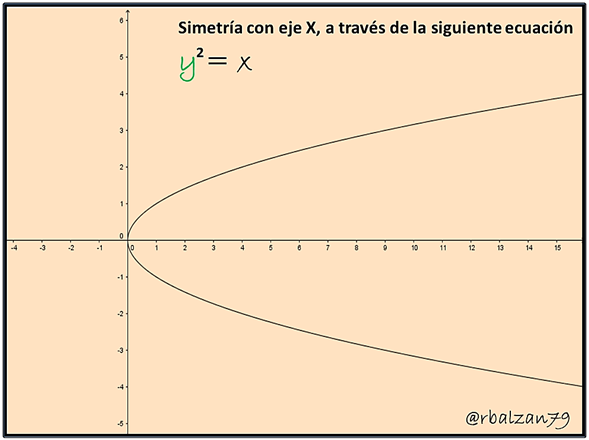
b.-) Simetría con el eje Y

Al desarrollar la simetría con respecto al eje de las X, podemos determinar, que si una determinada ecuación no experimenta cambios cuando sustituimos la variable X por –X, entonces para este caso dicha curva será simétrica ahora al eje de las Y.

c.- Simetría con respecto al origen

Si tenemos un determinado punto P(x, y) perteneciente a la curva, entonces para que dicha curva sea simétrica con respecto al origen (O) de las coordenadas del plano, debe existir otro punto P´ (a,b), sobre esta curva, de manera que (O) represente el punto medio del segmento PP´, en donde mediante las formulas:

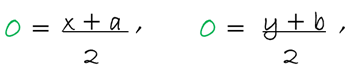
En donde a= -x y b = -y, por lo tanto, las coordenadas de P´(-x, -y) y debido a que dicho punto P´ se encuentra sobre la curva, sus respectivas coordenadas deben satisfacer la ecuación de dicha curva, es decir, para que pueda existir simetría entre la curva y el origen, la ecuación de la gráfica no debe experimentar alteraciones al momento de reemplazar tanto las variables x por –x , así como y por –y.

3.- Extensión de una curva

Mediante este análisis podemos expresar o determinar los intervalos de variación para (x , y), para los cuales tomen valores reales, así podríamos obtener la localización de manera general de dicha curva en el plano, además podemos saber si la curva es cerrada o si por lo contrario se extiende indefinidamente.

Para nosotros poder determinar los intervalos para los cuales los valores de (x , y) sean reales, debemos simplemente resolver la ecuación dada tanto para y, en términos de x, así para x en términos de Y.

4.- Asíntotas

Si tenemos una curva en el plano, y para la misma existe una recta de manera que un punto de dicha curva se aleja indefinidamente del origen de dicho plano coordenado, y la distancia de este punto de la curva con respecto a la recta decrece continuamente hasta tender a cero, entonces, esta recta la llamaremos o denominaremos asíntota de la referida curva, por lo tanto, una curva cualesquiera que pueda tener una asíntota la misma no es cerrada o de extensión finita, por lo contrario se extenderá indefinidamente aproximándose a la asíntota cada vez más a medida que la misma se extienda más y más a través del plano coordenado.

La línea recta denominada asíntota puede ser paralela o coincidir con el eje de las X, cuando esto ocurre la llamaremos asíntota horizontal; pero cuando coincida con el eje de las Y, será nuestra asíntota vertical, y si por el contrario no es paralela a ninguno de los ejes del plano coordenado tendremos una asíntota oblicua. Es importante resaltar que una curva puede no tener ningún tipo de asíntotas, es decir, no todas las curvas pueden llegar a tener asíntotas, pero lo importantes es, que si una determinada curva pueda llegar a tener una o mas asíntotas, esto sería de gran ayuda en el momento de poder dibujar o construir la gráfica o espacio geométrico de dicha curva, en el ejercicio de construcción de una curva observaremos las asíntotas presente en dicha curva.

5.- Construcción de curvas

Con anterioridad hemos podido desarrollar varios aspectos mediante el estudio de una ecuación, con la finalidad de poder estudiar el comportamiento de la misma mediante su representación gráfica, ahora tomaremos cada uno de los pasos antes señalados con algunos otros que desarrollaremos a continuación con el propósito de poder construir la curva de una determinada ecuación o expresión algebraica dada, por lo tanto, tenemos:

1.- Poder determinar las intercepciones con cada uno de los ejes del plano coordenado.

2.- Determinar la simetría de la curva tanto con cada uno de los ejes como el origen del plano coordenado.

3.- Determinar la extensión de la referida curva.

4.- Debemos determinar las ecuaciones de las asíntotas tanto verticales como horizontales de la curva, si las tiene.

5.- Para poder tener una gráfica adecuada debemos calcular las coordenadas de una cantidad de puntos suficientes para tal fin.

6.- Por último, debemos realizar el trazado de la respectiva curva en el plano coordenado.

Ejercicio 1

Construir la curva de la siguiente ecuación:

5.- Calcular las coordenadas de algunos puntos de la curva:

Para buscar algunas coordenadas de ciertos puntos para constituir la gráfica de la curva, podemos utilizar la ecuación de Y en función de X , debido a que nos suministra la mayor información con respecto a los intervalos para los cuales los valores de (x , y) deberían ser números reales.

6.- Construcción de la curva: con la ayuda de GeoGebra 5.0 , PhotoScape, PowerPoint y Paint, el siguiente gif animado:

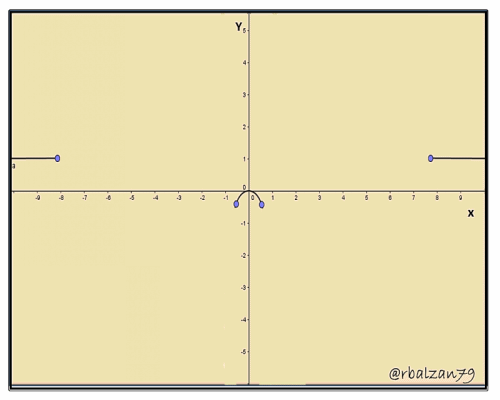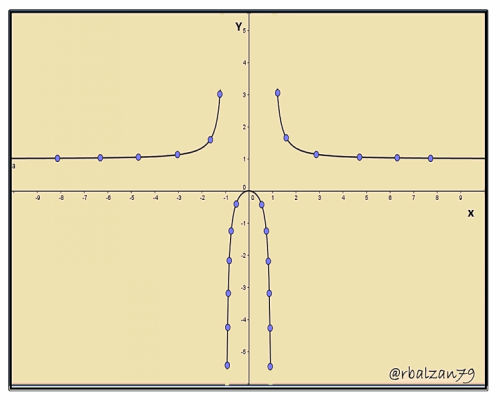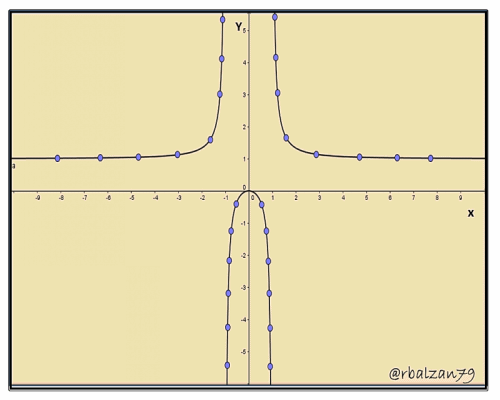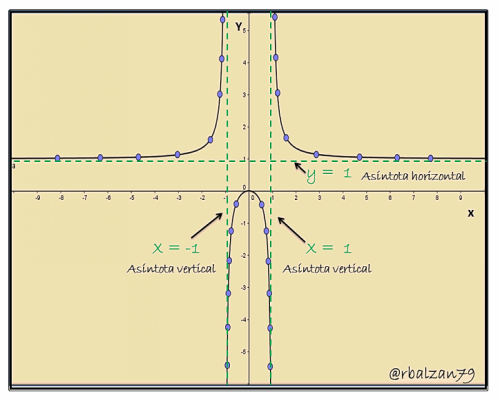
Ahora analizaremos el segundo planteamiento fundamental antes descrito:

Poder dar condiciones para los puntos de una determinada curva es como dar una ley la cual deben cumplir a cabalidad los puntos de dicha curva, en pocas palabras, tales puntos deben satisfacer la ley particular de la curva a la cual ellos pertenecen, por lo tanto, una curva la definimos como el lugar geométrico de todos aquellos puntos que puedan satisfacer una o más condiciones geométricas dadas.

Ecuación de una gráfica o lugar geométrico

Para iniciar debemos tener en cuenta que denominamos ecuación de un lugar geométrico en el plano coordenado a una ecuación del tipo:

Analíticamente para poder obtener la ecuación de un determinado lugar geométrico o gráfica, debemos seguir el siguiente procedimiento:

1.- Si tenemos un punto cualesquiera P de coordenadas (x,y), el mismo debe satisfacer la condición o condiciones dadas, entonces, el mismo debe pertenecer al lugar geométrico de la ecuación que queremos establecer.

2.- Debemos expresar de forma analítica, la condición o condiciones dadas a través de una ecuación(es) evidentemente en las coordenadas variables (x,y).

3.- Observamos la ecuación obtenida, si es necesario, la simplificamos para que pueda tomar la forma (*).

Ejercicio 2

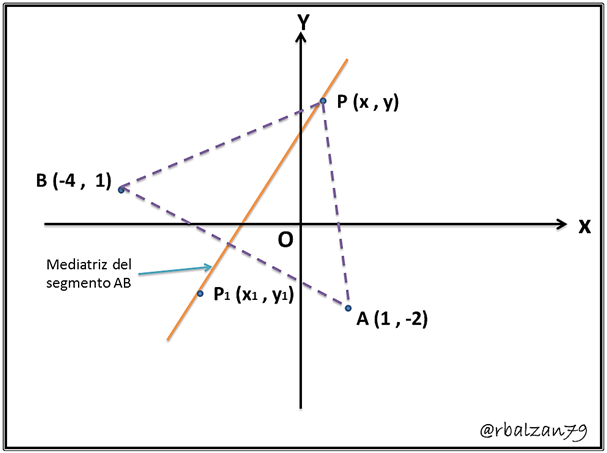
Ahora encontraremos la ecuación del lugar geométrico de un determinado punto el cual se mueve de tal forma que el mismo siempre equidiste de dos puntos conocidos o dados, los cuales son: A(1, -2) y B(-4, 1).

Como expresamos anteriormente, donde P(x,y) representa un punto cualesquiera del lugar geométrico, por lo tanto, podemos decir, que este punto P, debe cumplir o satisfacer la condición geométrica en donde los segmentos originados por PA y PB tengan la misma longitud, es decir:

Por medio de la fórmula para determinar la distancia o longitud entre dos puntos en el plano, analizada en la pasada publicación tenemos:

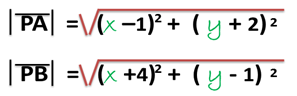
Por lo tanto, la condición geométrica antes descrita (A), la cual analíticamente la podemos expresar mediante la siguiente ecuación:

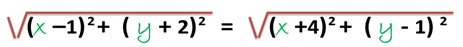
Al observar la ecuación obtenida, debemos realizar una serie de procedimiento (conocimientos previos) con la finalidad de simplificarla, entonces elevando al cuadrado ambos lados de la igualdad iniciamos con el desarrollo de la reducción de dicha ecuación:

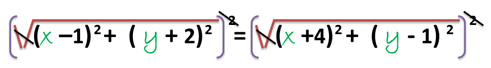
En la figura que a continuación se muestra notamos el lugar geométrico, el cual es una perpendicular a nuestro segmento AB en su centro o punto medio, por lo tanto, el punto que equidista entre ambos punto A y B, es decir, la mediatriz de dicho segmento AB.

Conclusiones

1.- La geometría analítica plana es nuestro fundamento o base principal para la comprensión de las distintas figuras geométricas presente en nuestro entorno, por lo tanto, para las matemáticas representa el lenguaje práctico y analítico que aporta a innumerables áreas del conocimiento y saber humano, es importante siempre resaltar este aspecto, ya que nuestros estudiantes deben tener muy claro el objetivo principal por el cual se formar, se educan, para continuar con la gran tarea de transmitir conocimientos a futuras generaciones, y la enseñanza de la geometría analítica estará por siempre entre nosotros.

2.- La representación gráfica en el amplio campo tanto de las matemáticas como en distintos campos del intelecto de la humanidad es muy valiosa, pero en ocasiones olvidamos las raíces de sus fundamentos, así como lo importante que es para cualquier estudiante o persona poder comprender o interpretar una determinada gráfica o lugar geométrico de una ecuación, sin embargo, la geometría analítica en general pero en particular la plana, nos brinda y nos brindará las herramientas necesarias para ir fortaleciendo tal importante comprensión y aprendizaje, ya que poder realizar el estudio de una ecuación o expresión algebraica con la finalidad de perfeccionar nuestro trazado al momento de realizar una gráfica es importante, conocer puntos como la intercepción, simetría, extensión, asíntotas de una curva con los ejes coordenados en el plano, nos permite poder realizar un estudio particular y comprobar que la gráfica y su ecuación estén en la más cercana armonía posible.

3.- Es importante destacar que nos encontramos con ecuaciones las cuales no poseen gráfica, dentro de un sistema coordenado real, también podemos encontrar que una determinada curva puede poseer más de una asíntota tanto vertical como horizontal, como también puede no tenerlas (asíntotas), esto por colocar algunos importantes ejemplos de los conocimientos obtenidos, también podemos resaltar nuevamente el hecho del engranaje de los conocimientos previos con los nuevos, en el recorrido de esta publicación nos encontramos con varios procedimientos necesarios para poder adquirir nuevos conocimientos, por ello el docente debe siempre estar atento para que nuestros estudiantes no se queden arrezagados al momento de seguir avanzando en el desarrollo de un determinado aprendizaje geométrico o matemático.

4.- La determinación de la ecuación de un lugar geométrico, nos ayuda a comprender la reciprocidad gráfica-ecuación, por lo tanto, para nuestros estudiantes es de gran ayuda conocer esta reciprocidad ya que le permitirá un mejor análisis y comprensión al momento de poder trazar una determinada curva o comprender el significado algebraico de la ecuación que da origen a un determinado lugar geométrico.

5.- La sociedad moderna de la ciencia y del saber humano en general, han encontrado en la gráfica y en la determinación de su ecuación, desde el punto de vista analítico toda la versatilidad posible para poder ampliar sus estudios con respecto a una determinada área de interés y desarrollo en pro de la humanidad, sigamos expandiendo los conocimientos matemáticos desde nuestras aulas de clases para que el futuro de las próximas generaciones sea lo más sólida posible en cuando a sus conocimiento, esto le garantizara sin dudas, su permanencia en este tan complejo universo.

Nota: Todas las imágenes y gifs fueron elaborados usando las aplicaciones Paint, Power Point, GeoGebra y Photoscape.

Referencias Bibliográficas

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

Autor: @rbalzan79.