Movimiento de un proyectil con simulación Phyton

Figura elaboración propia en Microsoft Word
En esta oportunidad voy a presentar un código realizado con el software libre Python, que puede caracterizar la trayectoria de un proyectil, en condiciones ideales.

Introducción
El propósito es presentar algunas instrucciones y sugerencias cortas para mejorar el aprendizaje del movimiento de un proyectil, al cualquier nivel educativo. Este tema, es parte de la cinemática y es bastante común en los cursos de física clásica, y también es visto por muchos estudiantes de cualquier nivel de estudios que están cursando física en las carreras de ciencias o ingenierías.
La propuesta es emplear el desarrollo de un código aplicado y ejecutado en el software Phyton. Es oportuno destacar que dicho software es una herramienta de libre acceso y se puede descargar desde Internet, aunado a una cantidad de información que puede ayudar al programador a crear cualquier actividad o programa. Se espera que esta idea sea de utilidad, para los profesores de Física a cualquier nivel de estudio.

Fundamentación teórica

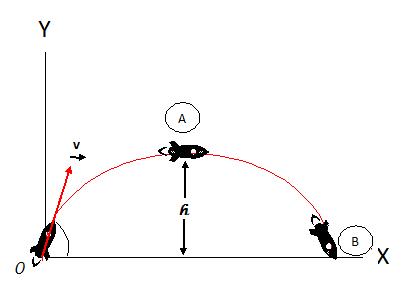
Se considera un proyectil (pelota de beisbol, balón de futbol, bala de cañón, bala de pistola, etc), que sale desde el piso en campo plano, que es disparado con una velocidad inicial Vi y regresa al mismo nivel (Serway, 2008). La trayectoria del proyectil siempre es una parábola como se muestra en la figura 1.

Figura 1 Proyectil lanzado sobre una superficie plana. Serway (2008). Imagen escaneada del texto
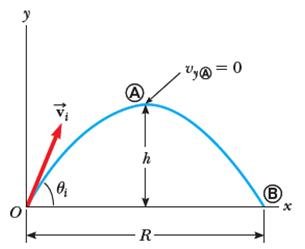
Por consiguiente se tienen unos parámetros que son necesarios para describir el movimiento de proyectil y son los siguientes; la altura máxima (ecuación 1), el alcance (ecuación 2) y el tiempo máximo (ecuación 3):
(1)
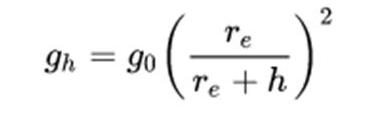
(2)
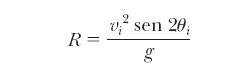
(3)

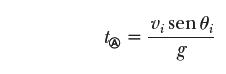
La trayectoria de un proyectil es parabólica y la ecuación de la trayectoria del proyectil que describe este movimiento (no se consideran el roce con el viento ni otras fuerzas adicionales asociadas con el movimiento de la tierra) es dada por: referencia: Alonso (1970):

(4)
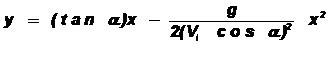
O bien
(5)

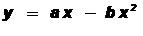
Donde los puntos notables en la trayectoria de un proyectil son los siguientes:

1. La altura máxima que alcanza.
2. El tiempo de vuelo de la partícula. Sería el tiempo máximo ecuación (3) multiplicado por 2. Tv= 2*tmax
3. La distancia máxima o el alcance máximo horizontal que recorre.

Ventajas del uso del software
En la actualidad el uso de software libre, abarata los costos de inversión en educación, investigación y desarrollo de las ciencias. referencia: García (2008). En la enseñanza de las ciencias unas de las herramientas más usadas es la programación, debida a que con ella se facilita el proceso de teorización, ya que modela fenómenos y se recogen información que después será analizada y procesada para construir teoría o verificar el comportamiento de un fenómeno en particular (Lab!).
Por esta razón, el profesor de física, debe desarrollar destrezas y habilidades en el uso de software, que le permitan la elaboración de códigos computacionales para relacionar los principios teóricos con la práctica de los fenómenos físicos estudiados. La programación facilita el proceso de conceptualización por medio de simulación de modelos físicos para la resolución de problemas.

Características preliminares del Python

Esta introducción consta de dos partes:

1. Preparar tu ordenador para que puedas escribir los códigos. Aprender a programar en códigos Python.

2. Disfruta haciendo tus propios códigos-programas.

Para empezar, se necesita instalar el programa, Python y sus librerías o módulos necesarios. Python es un lenguaje de programación fácil de aprender y poderoso. Se trata de software libre (freeware) y existe para todos los sistemas operativos.

Tiene estructuras de datos de alto nivel eficientes y un enfoque simple pero efectivo para la programación orientada a objetos. La elegante sintaxis y el tipado dinámico de Python, junto con su naturaleza interpretada, lo convierten en un lenguaje ideal para el desarrollo de scripts y de aplicaciones rápidas en muchas áreas en la mayoría de las plataformas.www.python.org

Existen muchas versiones de Python. Puede ser complicado escoger las versiones adecuadas y que luego trabajen juntas. El código desarrollado en este trabajo fue ejecutado en la versión de Python 3.4. Python viene con su propio editor y entorno de trabajo para desarrollar código.

Se pueden enlistar muchas características del lenguaje de programación Python. De manera particular se enumeran algunas que permiten a los estudiantes comenzar a programar de manera inmediata y sencilla: [www.python.org]

• Se trata de un lenguaje interpretado, de modo que se puede usar de modo interactivo o bien a través de la construcción de un script.
• Cualquier script puede ser utilizado como un módulo, es decir, una función u objeto que ya se construyó en algún archivo puede ser importada desde cualquier otro.
• Cuenta con librerías o módulos para cálculo numérico (Numeric, numpy) y aplicaciones científicas (scipy) así como para hacer aplicaciones interactivas así como animaciones gráficas (Tkinter, VPython, wxPython) cuya sintaxis es simple (como la del lenguaje en general)
• Existen en internet una gran cantidad de módulos, librerías, aplicaciones, documentación, etc.
• El lenguaje está orientado a objetos, los cuales se implementan de manera muy sencilla.
• No requiere declaración de variables: se declaran cuando se les asigna un valor que, obviamente, puede cambiar durante la ejecución.
• Los apuntadores son algo natural en Python y están asociados a los datos que tienen estructura interna (listas o arreglos).
• Las listas, son objetos muy flexibles que pueden contener simultáneamente cualquier tipo de dato escalar, nombres de funciones (apuntadores), otras listas, cadenas de caracteres, etc. Las librerías de uso numérico, como numpy, utilizan las listas y muchas de sus propiedades.
• Existen en internet una gran cantidad de módulos, librerías, aplicaciones, documentación, etc.

Aplicación con Python
Ahora bien se desarrolla el script en Python de este lanzamiento de proyectiles, sin tomar en cuenta el roce con el aire, ni los efectos que pueda influir la rotación de la Tierra. A continuación se muestra un código describiendo los pasos para generar la simulación del movimiento parabólico:

#Importamos todas las librerías necesarias
from matplotlib.pylab import *
import matplotlib.pyplot as plt
import numpy as np
from math import *
from sympy import *
from sympy.plotting import *
from time import *
from scipy import *
asctime()
clock()
#introducimos los datos
while True:
    try:
        β=float(input("introduzca el ángulo en grados β = "))
        except ValueError:
        print ()
        print("Cantidad Incorrecta")
        print ()
        continue
    break
while True:
    try:
        vi=float(input("introduzca la velocidad inicial en (m/s) vi = "))

    except ValueError:
        print ()
        print("Cantidad Incorrecta")
        print ()
        continue
    break
print ()
θ=((β*pi)/180)
print ("θ=",θ)
g=9.81 # m/s**2
print ()
a=tan(θ)
b=((g)/((2*vi**2)*cos(θ)**2))
print ()
ymax=(vi**2)*(np.sin(θ)*sin(θ))/(2*g)
xmax=(vi**2)*(np.sin(2*θ))/(g)
print ("................................................................................")
print ("................................................................................")
tmax=(vi*sin(θ))/(g)
tv=2*(tmax)
# Salidas de los datos calculados
print (str("La altura máxima  alcanzada por el proyectil es: Ymax")+" = "+str(ymax)+" m")
print (str("El alcance máximo horizontal  del proyectil es: Xmax")+" = "+str(xmax)+" m")
print ("................................................................................")
print ("................................................................................")
print ("La altura máxima (m) alcanzada por el proyectil es: Ymax =",format(ymax,".2f"))
print ("El alcance máximo horizontal(m) del proyectil es: Xmax =",format(xmax," .2f"))
print ("................................................................................")
print ("................................................................................")
print ("El tiempo máximo t1max (s) que alcanza el proyectil para el ángulo β es: t1max =",format(tmax,".2f"))
print ("El tiempo de vuelo t1v(s) que alcanza el proyectil para el angulo β es: t1v =",format(tv,".2f"))
print ("................................................................................")
print ("................................................................................")

# Definimos la ecuación de la trayectoria
def f(x):
    return(a*x-b*x**2)
x=np.linspace(0,xmax,500)
#creamos la figura
plt.figure("FISICA APLICADA",figsize=(10,8),dpi=80,facecolor="y",edgecolor="c")   
plt.axes(axisbg="orange")
# añadimos el titulo
title("LANZAMIENTO DE PROYECTILES", 
fontsize=15,color="blue",verticalalignment="baseline",horizontalalignment = "center")  
# añadimos el subtitulo
plt.suptitle("CINEMATICA",fontsize=20,color="red")

#añadimos las etiquetas de los ejes
xlabel("xmax",fontsize=20,color="red")                                      
ylabel("ymax",fontsize=20,color="blue")
#añadimos texto
plt.text(((np.argmax(f(x)))/2),np.max(f(x))+1,"vi=",fontsize=10)
plt.text(((np.argmax(f(x)))/2)+11,np.max(f(x))+1,(str(vi)+"m/s"),fontsize=10)
#mostrar la fecha y la hora actual formateadas :",asctime()
#mostrar el tiempo real de ejecucion de este proceso :",clock()
plt.text(2,np.max(f(x))+1,("fecha/hora:"+str(asctime())),fontsize=10,color="green")
plt.text(2,np.max(f(x))-1,("tiempo(s):"+str(clock())),fontsize=10,color="blue")

# Añadimos la rejilla en la gráfica
plt.grid(True)                                                              
plt.grid(color = '0.5', linestyle = '--', linewidth = 1)
# Añadimos los ejes 
# plt.axis("tight")                                     
                 
# dibujamos y ponemos etiquetas a la gráfica
plt.text(3,1,β,fontsize=10)
plt.plot(x, f(x), "red", linewidth = 2, label = (str(β)+"º"))   
# añadimos la leyenda
plt.legend(loc = 4,fontsize=10)                                                         
#anotaciones en el gráfico
plt.annotate('Altura Máxima',
xy = (xmax/2, ymax),
xycoords = 'data',
xytext = (-70, -50),
textcoords = 'offset points',
arrowprops = dict(arrowstyle = "->",
connectionstyle = "arc, angleA = 0,armA = 30,rad = 50"),
# dibujar tabla dentro del gráfico
valores = [[format(np.max(xmax),".2f"),format(np.min(ymax),".2f")]]
etiquetas_col = ["xmax (m)", "ymax (m)"]
plt.table(cellText=valores, colLabels = etiquetas_col, colWidths = [0.15]*len(f(x)),loc='upper right')
# guarda la gráfica con 300dpi (puntos por pulgada)en python34-ejemplos curso python
#plt.savefig("figura_Lanzamiento Proyectiles_1.pdf", dpi = 300)            
# mostramos en pantalla la gráfica
plt.show()

En la figura 2, se muestra el resultado arrojado por el código presentado anteriormente. En esta se observa claramente la trayectoria parabólica de un proyectil para una velocidad inicial de 50 m/s y un ángulo de disparo de 45°.

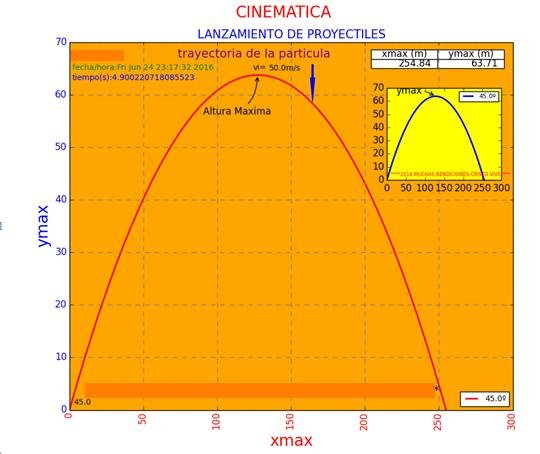
Figura 2. Representación grafica mostrado. Ejemplo de funcionamiento con valores de la velocidad vi = 50 m/s, β = 45º

Conclusiones
El enfoque propuesto consiste en que, además de la posibilidad de ver los fenómenos desde otro punto vista, los estudiantes cuenten con el apoyo tecnológico adecuado, con el manejo de software libre (Python)en el laboratorio o en cualquier lugar donde tenga un computador.

Las simulaciones que se realizan en Python, tienen la ventaja de reproducir con gran exactitud la mayoría de los fenómenos físicos que se estudian en las aulas. Esto permite que el estudiante se familiarice con el fenómeno estudiado, desarrolle sus propios modelos, para simulaciones o solución de problemas que se proponen en los cursos de física y por supuesto a bajo costo.

Referencias

1. Alonso M, Finn E. (1970). Física Mecánica. Vol. 1. Fondo educativo interamericano S.A
2. García Corzo, Pablo (2008). «Proyecto Physthones». Simulaciones Físicas en Visual Python (0.1). Un libro libre de Alqua.
3. Lab!, Laboratorio de innovación educativa (2012). «Aprendizaje cooperativo: Propuesta para la implantación de una estructura de cooperación en el aula». [Consultada Agosto 2017].
4. Página de Python, http://www.python.org
5. Serway Raymond A. y Jewett Jr. John W. (2008). Física para ciencias e ingeniería. Editorial Cengage Learning Editores S.A. de C. Volumen 1. Séptima edición.
   Otras referencias de interés
   J.F. Rojas y M.A. Morales. Física computacional: una propuesta educativa. Facultad de Ciencias Físicas y Matemáticas, Benemérita Universidad Autónoma de Puebla, Edif. 190 18 sur y Av. San Claudio, C.U., Col. San Manuel, 72570 Puebla, Pue.
   A. Bake, Computational physics education with python. Computing in Science y Engineering (2007).
   Newman, Mark (2013). Computational Physics. CreateSpac