Hola estimada comunidad de stem-espanol, les envío un gran saludo. En esta oportunidad coloco la segunda fase de este post, que está comprendida en dos etapas. La segunda etapa que viene a continuación del primer post, explicará el uso del software Traker y una tercera etapa que explicará el uso del software libre Python para esta fenomenología. Finalmente se hará un análisis comparativo de las tres herramientas de estudio.

Imagen Propiedad de @germanmontero

Etapa II: Uso del Tracker

En este caso, al mismo tiempo que se realizaba la experiencia con el uso del sensor, el analizador de datos y la calculadora, se capturaron videos del balón de fútbol en caída libre, sin y con velocidad inicial, mediante una cámara digital de 14.0 Mega-pixels, Marca SANYO modelo VPC-T1496.

Cabe destacar, que Tracker es un software libre disponible en la internet, de fácil manejo y debe ser instala en la plataforma Java. Primero se debe descargar el Tracker en la computadora. Luego de grabar un vídeo del movimiento del balón, se procede a mover el vídeo dentro del programa al área de trabajo, que consiste en una ventanilla, la cual puedes acercar o alejar la imagen del vídeo, utilizando la tecla de control y el scroll.
Aquí dejo unos pequeños pasos:

• El vídeo se puede seleccionar una parte para analizar lo más importante de la trayectoria.
• Seguido de esto se toma una masa puntual disponible en la barra de herramienta.
• Se calibra la medida
• Se ajusta el sistema de coordenadas en el objeto, colocando el cero en el balón.
• Se captura los datos y se registran de manera sencilla, mostrando inmediatamente la gráfica en el programa

Para instalar el Tracker, pueden acceder a este link Tracker. Aquí pueden instalar el programa, ademas de poseer un excelente tutorial para analizar vídeos y presentaciones de conferencias sobre el uso de experiencias en Tracker.

Después de la grabación, se procedió a analizar el vídeo utilizando el software Tracker versión 4.87, así pues se logró digitalizar el movimiento de la caída libre del objeto. Este software computarizado dispone de una función avanzada que permite realizar el seguimiento del objeto, denominada Auto-Tracker, además de registrar su posición y su tiempo de manera secuencial sólo pulsando clic con el ratón conectado a la computadora, en nuestro caso una PC de medianas prestaciones. Una vez capturados los datos del vídeo, se grafican con el mismo programa y se analiza el comportamiento de la posición en función del tiempo. Se destaca la posibilidad de este software analizador de vídeos de disponer de la data resultante para ser utilizada con otros programas de capacidades gráficas más avanzados como los mencionados en la Etapa I de este estudio

Etapa III: Simulando la caída libre del objeto con el software Python

En esta etapa se realiza la modelación experimental que se desarrolló utilizando el software Python Python, conectado con algunas de sus librerías disponibles para realizar los códigos. En este caso se genera la gráfica de la altura versus el tiempo del movimiento en caída libre del balón de fútbol con su respectivo ajuste polinomial cuadrático y la simulación de los ensayos realizados anteriormente. Para esto, se tomaron en cuenta los datos adquiridos por el sensor de movimiento, a fin de calcular el valor de la aceleración de la gravedad terrestre. Por consiguiente, se presentan a continuación una breve descripción de los scripts correspondientes realizados con este software libre:

Descripción del algoritmo de cálculos y gráficas

En la línea 2 del código, se activa la librería matplotlib para que estén disponibles las funciones gráficast.
En la 3, se importa la librería numpy. En la siguiente línea se activa de la librería scipy el ajuste polinomial el cual se va a utilizar en el ajuste cuadrático de los datos.
Luego, en la línea 5 se abre el archivo que contiene los datos de tiempo y altura que alcanza el objeto en caída libre. En las líneas 6 y 7 se inicializan los arreglos que almacenan los datos del tiempo (x1), y la posición del objeto en caída libre (y1).
Después en el bucle for de las líneas de la 8 a la 11 se lee línea a línea los datos separados por una coma (,) tal como se hace en la línea 9. El resultado es que se almacena el tiempo y la altura en las variables x1 y y1 respectivamente. Al terminarse la lectura del archivo, finaliza el bucle for y en la línea 12 se cierra el archivo.
En la línea 13 se almacena en la variable sol (solución) el ajuste cuadrático de los datos almacenados en el archivo. En la línea 15 se imprime en pantalla la solución del ajuste cuadrático que regresa la función polyfit() de la librería scipy y en las líneas de la 16 a la 18 se imprime los valores de a, b y c de la ecuación: ax2+bx+c.
Ahora bien, en las líneas de código de la 22 a la 26 se define la función que grafica la función con los valores del ajuste cuadrático. En la línea 27 se utiliza linespace() de la librería numpy con la finalidad de suministrar datos entre un valor inicial y un valor final, en este caso se tomó 0.3 que es menor que el menor tiempo del archivo que contiene los datos y 1.1 que el mayor que el mayor de los tiempos en el mismo archivo.
En las líneas de la 29 a la 33 se muestra en el gráfico, el título con: plt.title(), la etiqueta del eje x con: plt.xlabel(), y la etiqueta del eje y con: ylabel(). Seguidamente, se activa la rejilla con plt.grid() y finalmente se enciende la visualización de varios gráficos en uno sólo con plt.hold(True). Todas estas funciones de la librería matplotlib.
La gráfica de los datos ajustados se realiza con la instrucción de la línea 34. Y en las líneas de 36 a la 41 se muestran todos los datos, tal como están en el archivo de datos. En la línea 42 se utiliza la instrucción plt.show(), de matplotlib, con la finalidad de que se muestren los gráficos (ver cuadro 1)

Cuadro1

1  # Regresión cuadrática para la experiencia de Caída Libre
2  import matplotlib.pyplot as plt
3  import numpy as np
4  from scipy import polyfit # Activa de la libreria scipy la función ajuste polinomial
5  mi_archivo = open("caida1.txt") # Abre el archivo caida1.txt que contiene los datos
6  x1=[]
7  y1=[]
8  for line in mi_archivo:
9   x, y = line.split(',')
10  x1+=[float(x)]
11  y1+=[float(y)]
12 mi_archivo.close()
13 sol=polyfit(x1,y1,2) # Agui se calculan los coeficientes del ajuste cuadrático
14 print("La ecuación de la regresión cuadrática es: ax**2+bx+c")
15 print("Sol=",sol)
16 print("a=",sol[0])
17 print("b=",sol[1])
18 print("c=",sol[2])
19 print("Los datos son:")
20 print("x1=",x1)
21 print("y1=",y1)
22 def f(x2): # Función que devuelve el valor de la altura con los datos del ajuste
23         a=sol[0]
24         b=sol[1]
25         c=sol[2]
26         return a*x2**2+b*x2+c
27 x2=np.linspace(0.3,1.1)
28 # Se traza la gráfica correspondiente a la ecuación de los datos ajustados
29 plt.title("Gráfica de Altura vs tiempo para caída libre")
30 plt.xlabel("Tiempo (s)")
31 plt.ylabel("Altura (m)")
32 plt.grid()
33 plt.hold(True)
34 plt.plot(x2,f(x2))
35 # Se grafican los datos del archivo
36 i=0
37 num_ele=np.size(x1)
38 print("Num Ele=",num_ele)
39 while i<=num_ele:
40        plt.plot([x1],[y1],"rv")
41        i+=1
42 plt.show()

Descripción del algoritmo de simulación

1. Se deben aperturar las librerías necesarias para comenzar el programa. Para este caso se utilizará el matplotlib en la línea 2
2. En la línea 3 del código, se activa la librería matplotlib para que estén disponible las funciones gráficas y se guarda en el alias plt.
3. Luego, en la línea 4 se abre el archivo que contiene los datos de tiempo y altura que alcanza el objeto en caída libre. Seguidamente, en las línea 5 y 6 se inicializan los arreglos donde se almacenarán los datos del archivo: en x1 se almacenarán los tiempos y en y1 las posiciones en el “eje y” del objeto en caída libre.
4. Después, en las líneas de la 7 a la 10 de código Python se ejecuta un bucle for que lee línea a línea los datos en el archivo los cuales están separados por una coma (,), ver línea 8. El resultado de este bucle es almacenar el tiempo y la altura en las variables x1 y y1 respectivamente. Al terminarse la lectura del archivo, es decir que no se consiguen más datos, se sale del bucle for y en la línea 11 se cierra el archivo.
5. En las líneas de la 12 a la 16 se inicializa el contador del bucle while, en la 13 se asigna a la variable alfa el número de datos que hay dentro del arreglo de alturas y1[ ]. En las líneas 14, 15 y 16 se dibuja el rastro de caída libre del objeto utilizando la función scatter de la librería matplotlib con todos los datos. Es notable destacar que aquí se mantiene la posición en el eje x=0 y el signo en el arreglo de y1[ ], se debe a que el objeto se mueve hacia abajo. En las líneas de la 17 a la 19 se definen las etiquetas del gráfico y finalmente en la línea 20 se muestra el arreglo de tiempos y en la 21 el de alturas. (ver cuadro 2).

Cuadro 2

1   # Programa que gráfica la posición de un objeto en caída libre
2   #
3   import matplotlib.pyplot as plt
4   mi_archivo = open("caida1.txt")                 
5   x1=[ ]                           
6   y1=[ ]                           
7  for line in mi_archivo:
8   x, y = line.split(',')
9   x1+=[float(x)] 
10  y1+=[float(y)] 
11 mi_archivo.close() 
12 i=0 # Se inicializa i
13 alfa=len(y1) 
14 while (i<alfa):
15      plt.scatter(0,-y1[i]) 
16      i+=1 
17 plt.title("Gráfica de Altura vs tiempo para un objeto en caída libre")
18 plt.ylabel("Altura (m)")
19 plt.xlabel("Posición en el eje x")
20 print ("t=",x1) 
21 print ("y=",y1)  
22 plt.show()

En La figura 5, se muestra el comportamiento del movimiento de la caída libre simulado con el programa Tracker. Los resultados obtenidos muestran que el balón tuvo un movimiento rectilíneo uniformemente acelerado, obteniéndose un valor de la gravedad de 9.9934 m/s^2 con velocidad inicial 0 m/s.

FIGURA 5. Gráfica experimental Tracker de la posición en función del tiempo con velocidad inicial=0. Imagen Propiedad de @germanmontero
La comparación entre la gravedad experimental de 9.934 m/s^2 con la gravedad aproximada de 9.806 m/s^2, arrojo un error experimental de 1.30 %.
En La figura 6, se muestra el comportamiento del movimiento de la caída libre simulado con el programa Tracker. Los resultados obtenidos muestran que el balón también posee movimiento rectilíneo uniformemente acelerado, obteniéndose un valor de la gravedad de 9.886 m/s^2 con velocidad inicial 0.3461m/s es decir de 34,61 cm/s.

FIGURA 6. Gráfica experimental Tracker de la posición en función del tiempo con velocidad inicial. Imagen Propiedad de @germanmontero

Para este caso, la comparación entre la gravedad experimental de 9.886 m/s^2 con la gravedad aproximada de 9.806 m/s^2, arrojo un error experimental de 0.80 %. En el mismo sentido, los resultados obtenidos con Python se muestran en las figuras 7 para el movimiento en caída libre vo=0 y la figura 8 para el movimiento vertical con velocidad inicial probable. En este caso se puede observar que el comportamiento de los dos movimientos es semejante a los obtenidos con las técnicas anteriormente explicadas.

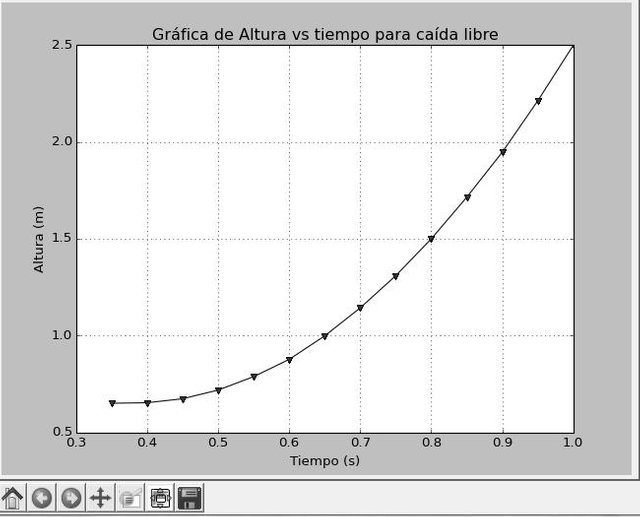
FIGURA 7. Gráfica obtenida del código Python correspondiente a la caída libre vo=0, Datos experimentales y ajuste cuadrático. Imagen Propiedad de @germanmontero

Resultado experimentales arrojados por el ajuste cuadrático
La ecuación de la regresión cuadrática es: ax^2+bx+c
Sol= [4.81367033 -3.65965626 1.34481765]
a= 4.81367032967
b= -3.65965626374
c= 1.34481764835

Estos valores dan como resultado un valor de la gravedad de 9,627m/s^2 teniendo como error experimental con la gravedad promedio de 9,806 m/s^2 un valor de 1.825%, lo cual se considera muy bajo y aceptable para este procedimiento.

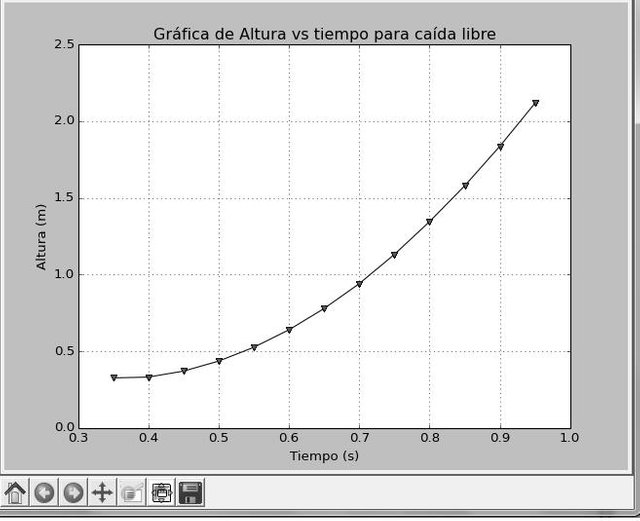
FIGURA 8. Gráfica obtenida del código Python correspondiente a la caída libre vo=inicial, datos experimentales y ajuste cuadrático. Imagen Propiedad de @germanmontero
Resultado experimentales arrojados por el ajuste cuadrático
La ecuación de la regresión cuadrática es: ax^2+bx+c
Sol= [4.91498362 -3.38395442 0.9016239 ]
a= 4.91498361638
b= -3.38395441558
c= 0.901623904096

Estos valores dan como resultado una magnitud de gravedad de 9,829 m/s^2 teniendo como error experimental con la gravedad promedio de 9,806 m/s^2, un error porcentual de 0.234%.
Por otro lado, se observa la simulación tipo fotográfica (de las exposiciones) del comportamiento en caída libre y con velocidad inicial del balón de fútbol. En la figuras 9 y 10 se muestra tales comportamientos, donde se ven más separados, al inicio del movimiento, los puntos cuando existe un impulso de velocidad inicial que incrementa la separación de desplazamientos entre los intervalos de tiempos iguales. Esta simulación tipo fotografía instantánea del movimiento en caída libre, lo realiza la función scatteer de las librerías del matplotlib.

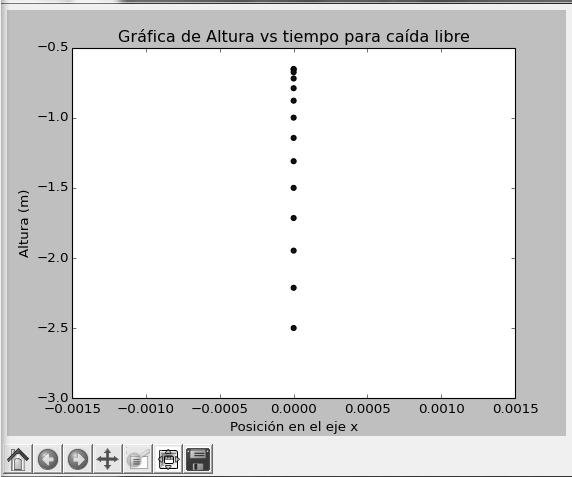
FIGURA 9. Diferentes posiciones del objeto en caída libre, utilizando la simulación con Python. Imagen Propiedad de @germanmontero

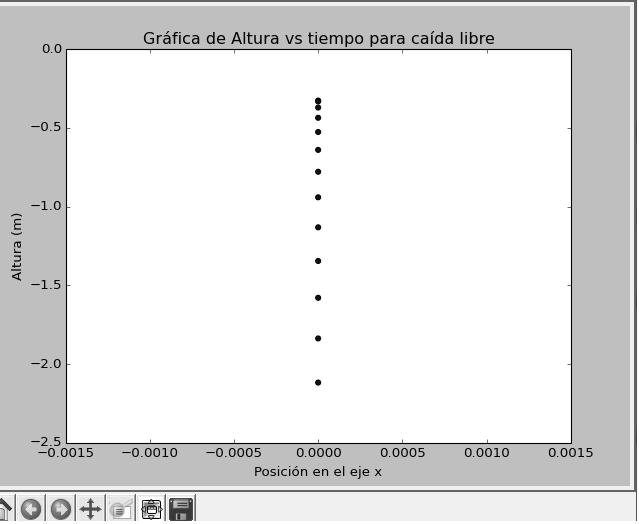
FIGURA 10. Resultados de diferentes posiciones del objeto con velocidad inicial utilizando la simulación con Python. Imagen Propiedad de @germanmontero

Se analiza que para los métodos experimentales e informáticos, utilizados en esta investigación, arrojaron errores muy bajos, confirmando la eficiencia para la adquisición y procesamiento de datos de estos métodos.
Así mismo la ventaja que tiene el programa Tracker, es que tiene la virtud de hacer sencilla la adquisición de los parámetros del movimiento en caída libre, por ejemplo se procesa en el mismo programa y se obtiene un ajuste cuadrático, cuyos resultados son excelentes. La comparación de resultados se presenta en la tabla II.

TABLA II. Comparación de resultados de los tres métodos. Imagen Propiedad de @germanmontero

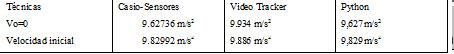
CONCLUSIONES

Un análisis comparativo, se realiza al saber que la calculadora Casio con sus sensor es más versátil para la adquisición de los datos y la graficación instantánea de ellos, en cambio utilizando el Traker tienen una opción llamada Auto-Track, que realiza automáticamente la recolección de datos pero depende de la calidad del video, que se debe grabar previamente. Por otro lado, en el software libre Python se pueden incorporar una serie de librerías que permiten mediante la elaboración de scripts, el ajuste matemático y simulación de los datos experimentales.
Ahora bien, al comparar los resultados obtenidos con la calculadora científica Casio ClassPad 300, y los software Tracker y Python, se comprobó que la selección del analizador de vídeo Tracker, además del software Python, pueden ser buenas herramientas didácticas para hacer experimentos y simulaciones de este fenómeno físico como es la caída libre de los cuerpos, con bajos recursos económicos.

REFERENCIAS

M. Sánchez. Siete cuestiones para divulgar y comprender aspectos de la caída libre. Latin American Journal Education. Vol 5. No.3 (2011).
E. Begeler. Experiment showing the motion of a falling object and the influence of air drag. Latin American Journal Education. Vol 3. No.1 (2009).
R. Serway y J. Jewwet. Física para Ciencias e Ingeniería. 7ma. Edición. Editorial Cengage-Learning. Volumen 1. (2009),
P. Tipler, y G. Mosca Física para la Ciencia y la Tecnología. (7ma. Edición. Reverte S.A). Vol 1. (2005).
Tracker. https://physlets.org/tracker/
Python. https://www.python.org/
H. Ohanian y J. Market Física para Ciencias e Ingeniería. 3 ra Edición. Editorial McGraw Hill / Interamericana. Vol 1. Mexico. (2009).