➿ El NÚMERO DE GRAHAM como el más grande entero aplicado en una demostración matemática: descripción y comentarios para especialistas y no-especialistas
3️⃣ ⮅▪️▪️▪️⮅ 3️⃣ El número más grande jamás usado en una demostración matemática seria 💻
En este artículo se hace una descripción del número que ostenta el Record Guinness de ser la mayor cantidad entera jamás usada en una demostración matemática en toda la historia de la humanidad [1]. El artículo introducirá información necesaria para comprender la representación matemática de este número usando el tecnicismo requerido en el área, aunque procurando también dosificarlo para público no matemático a través del uso de analogías y/o ilustraciones, sin sacrificar el formalismo necesariamente.
De entrada, hay que señalar que históricamente se han descubierto y acuñado cantidades asombrosamente grandes, bien sea a partir de objetos naturales y artificiales del intrincado mundo físico, o a partir del abstracto mundo de las matemáticas. Algunas de esas cantidades pudieran ser comunes y corrientes, mientras que otras pudieran representar toda una novedad. Por ejemplo:
| 1) Un millón | 1.000.000 | 106 |
| 2) Un billón | 1.000.000.000.000 | 1012 |
| 3) Un trillón | 1.000.000.000.000.000.000 | 1018 |
| 4) Un cuatrillón | 1.000.000.000.000.000.000.000.000 | 1024 |
| 5) Un quintillón | 1.000.000.000.000.000.000.000.000.000.000 | 1030 |
6) El número estimado de átomos que hay en el universo conocido: 10^82 = 10⁸². Se sabe que esto puede imaginarse como un 1 seguido de ochenta y dos ceros , y ello representa la cota máxima de átomos existentes en el universo observable. Al juzgar por el tamaño del espacio exterior y los objetos celestes, podría conjeturarse con esa cantidad 'parece poca', pero lo cierto es que es una cantidad extremadamente vasta [2].
7) El Gúgol ("Google", en inglés ) = 10^100 = 10¹⁰⁰. Es de este número de donde los fundadores de la famosa corporación transnacional "Google" se inspiraron para su nombre, quizá haciendo alusión metafórica a la cantidad de resultados que su motor de búsqueda puede generar [3].
8) La complejidad del árbol del juego de ajedrez: 10^123 = 10¹²³. En otras palabras, se refiere al número de partidas distintas que hay en el ajedrez. El valor presentado es un refinamiento reciente del número original, conocido como "Número de Shannon", que es 10¹²⁰ [5] [6]. La complejidad de este juego trae de relieve una magnitud gigantesca.
9) El Gúgolplex ("Googleplex", en inglés) = 10^gúglol = 10^10¹⁰⁰.... Demasiado grande... Considerando el hecho que el número de átomos del universo observable ronda los 10⁸², lo cual ya constituía una inmensa cantidad a la escala de todo nuestro mundo físico conocido, el gúgolplex es un 1 seguido, no de 80, sino de ¡gúgol ceros! (10¹⁰⁰), es decir, una cantidad indescriptiblemente grande:
10^10¹⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰
Esto implica que ¡no hay suficientes átomos en todo el universo conocido para que sea físicamente posible escribir los ceros que este número tiene!
No obstante, al juzgar por la magnitud del número que protagoniza este artículo, va a ser válido y necesario esforzar un poco el lenguaje para destacar su diferencias...
Y es que el gúgolplex sería poco más que cero, prácticamente un sinónimo retórico de la nada, una triste y remota insignificancia, una cantidad infinitesimalmente más microscópica si se le compara con el número que ostenta el record de ser el más grande entero jamás usado en matemáticas serias: el número de Graham, llamado así en honor a su descubridor, el matemático estadounidense Ronald Graham, quien aún vive, y lo calculó y publicó en 1977 [1].

(Ronald Graham, 1935-actualidad. Matemático estadounidense acreditado por la Asociación Matemática de los Estados Unidos, autor del "Número de Graham", obtenido tras años de revisión de su propio trabajo. Fuente: Googology.wikia.com)
El número es una solución a un problema matemático complejo de la teoría de Ramsey, una rama de las matemáticas, cuyo enunciado se cita a continuación [7]:
Considérese un hipercubo n-dimensional, y conéctese cada par de vértices para obtener un grafo completo con 2^n vértices. Posteriormente, coloréese cada una de las aristas de negro o de rojo. ¿Cuál es el menor valor de n para el cual toda manera de colorear las aristas necesariamente da lugar a un subgrafo completo de un solo color con 4 vértices que forman un plano?
Para propósitos didácticos, se provee a continuación una explicación más dosificada:
Un cuadro es un objeto bidimensional y un cubo es el objeto análogo al cuadro, pero en tres dimensiones. Un hipercubo, por su parte, es un objeto análogo al cuadro y al cubo, es decir, éstos dos últimos también son hipercubos, pero el término "hipercubo" puede aplicar a cualquier cantidad de dimensiones, por lo que se dice que puede ser de n-dimensiones.
Se trata de descubrir la cantidad máxima de dimensiones en las cuales el hipercubo mantiene la propiedad de permitir que sus aristas puedan ser coloreadas de un modo particular ("un subgrafo completo de un solo color con 4 vértices que forman un plano").
Dado que en el mundo tridimencional y bidimensional es posible comprobar su solución fácticamente, y en el mundo algebraico también se puede obtener la solución para muchas dimensiones, inicialmente se podría suponer que no existe una dimensión en la cual no aplique la propiedad. Tal razonamiento es erróneo, pues no parte de un proceso deductivo y requiere de una demostración matemática.
De allí el planteamiento del problema. La solución es que sí existe un límite de dimensiones para ello y el resultado es el Número de Graham, que es la cota superior de la solución, esto es, el valor máximo del conjunto de valores que solucionan el problema.
El asunto es que no hay adjetivos para describir de manera única lo grande que es este número ya que es prácticamente un axioma el hecho de que sobrepasa todos los límites físicos conocidos y la capacidad del cerebro humano para procesar tamaña magnitud. Su autor a veces se refiere a él como "ridículamente grande".
Incluso para representarlo, hay que usar una notación menos convencional a la habitualmente usada, debido a las limitaciones de esta última para lograr ese cometido. Se usa la notación de Knuth, la cual se explica a grosso modo a continuación, junto con una explicación lógica de su aplicación en el cálculo del colosal número. He aquí el razonamiento:
-Se sabe que 10³ puede escribirse como 10^3, es decir, 10 x 10 x 10 que es 1.000.
-Análogamente, 3^3^3 se puede traducir a 3^27, lo que calculado da: 7.625.597.484.987 (siete billones, seiscientos veinticinco mil, quinientos noventa y siete millones, novecientos ochenta y siete unidades).
- Probablemente ya es imposible para una persona escribir 3^27 trazas de algo (ejemplo: escribir 7.625.597.484.987 cantidad de guiones), dado que es un número muy elevado, mayor a 1.000 veces la cantidad de seres humanos habitando La Tierra.
-Aunque sea imposible dibujarlo o detallarlo, por lo menos es posible tener el concepto de lo que son siete (7) billones y mantener su representación con torres de exponentes.
-Cuando estos aspectos se combinan, es posible usar la notación de flechas inventada por Knuth.
-En este sentido, 3^3 puede ser reescrito usando la notación de flechas así: 3 ↑ 3, donde el primer valor es la base y el segundo el exponente, siendo la flecha sola un operador de potencia.
-No obstante, cuando se introduce una segunda flecha, estas se vuelven un operador de potenciación iterada, por lo cual 3 ↑↑ 3 quiere decir que el tres a la izquierda es el valor de la base y también de los exponentes, mientras que el tres a la derecha es la cantidad de torres de exponentes, contando también a la base. Ejemplos:
5 ↑↑ 4equivale a5^5^5^5en notación convencional y se lee "5 a la 5 a la 5 a la 5". En notación Knuth también equivale a5↑(5↑(5↑5)).3 ↑↑ 3equivale a3^3^3en notación convencional, y se lee "3 a la 3, a la 3". En notación Knuth también equivale a3↑(3↑3).
-Si añadimos una flecha más (↑), la expresión quedaría así: 3 ↑↑↑ 3, lo que algebraicamente se puede expresar como 3↑↑(3↑↑3), es decir, una torre de 3↑↑3 veces 3. En otras palabras, es igual a la serie "3^3^3 ... 3^3^3", que posee un total de 7.625.597.484.987 términos.
-Podría visualizarse esto imaginando un torre de 3 con más de siete billones de pisos (este cálculo es ya una increíble barbaridad).
-¿Y qué si se pudiera hacer ese hipotético cálculo e imaginar una torre de 3 que contenga esa cantidad de pisos, es decir 3 ↑↑↑ 3 términos!?
-Esto es lo que significa la expresión 3 ↑↑↑ 4.
-¿Y una torre de 3 que contenga 3 ↑↑↑ 4 pisos?
-Pues, simplemente 3 ↑↑↑ 5.
-¿Y qué tal si repetimos este mismo proceso un total de 3 ↑↑↑ 3 veces?
-La respuesta es la (inconcebible) cantidad de 3 ↑↑↑↑ 3.
...Pero eso no es todo...
-Imagínese ahora una serie de 3 ↑↑....↑↑ 3 donde hay 3 ↑↑↑↑ 3 cantidad de flechas.
-Ahora, tómese ese resultado y úselo para representar la cantidad de flechas de una nueva serie 3 ↑↑....↑↑ 3
-Repita ese proceso 62 veces.
-Se ha llegado al número de Graham.
Esta cantidad indescriptiblemente grande es una función recursiva, en realidad. Toma el valor calculado como nuevo argumento para la misma función, lo cual provoca un crecimiento exponencial y explosivo cada vez que se evalúa y obtiene un nuevo valor o serie.
Formalmente, su definición se inserta a continuación (véase imagen siguiente):
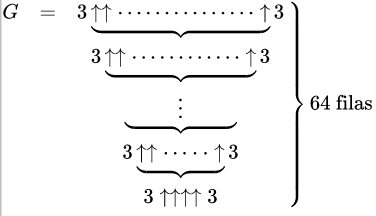
(Definición formal del Número de Graham en notación Knuth. Fuente)
Cada expresión horizonal es una serie de la función recursiva G cuya profundidad se denota con un subíndice. Se parte desde la expresión G0 al fondo del la gráfica cuyo valor es 3 ↑↑↑↑ 3. Esta se utiliza para representar el valor de potenciación iterada (número de flechas) de la siguiente serie G1, y el valor de esta se aplica, a su vez, a la siguiente serie G2 y así sucesivamente (...) hasta alcanzar la serie G64 que obtiene finalmente el valor del Número de Graham.
Pues éste es resultado de la función. El valor puede no ser tan relevante por sí mismo como por el proceso matemático implicado para su obtención que revela la inmensa dificultad para conseguir soluciones exactas a los problemas de la teoría de Ramsey. Se muestran ahora algunos de sus últimos dígitos, para el alcance de la finitud humana: ...2.464.195.387, aunque también existen fuentes que difunden cerca de 500 dígitos de este número [8].
Se ha sugerido que tras este hallazgo se han descubierto otros números o funciones incluso más grandes, tal como el así llamado "número Árbol(3)" [9], lo cual recuerda lo asombrosas que pueden ser las matemáticas y lo difícil que es para el humano entender el concepto de la infinitud. El autor de este icónico número lo explica mejor:
"El Número de Graham realmente no está más cerca del infinito que el número uno. Simplemente no has empezado todavía. Incluso aunque te tomara muchos pasos para llegar al Número de Graham, se lleva muchísimo más, infinitamente más, llegar al infinito"
Roland L. Graham
Con todo, como se ha se ha reiterado, el Número de Graham ganó el conocido record mundial por ser el más alto valor con aplicación matemática, y probablemente continuará como 'el más grande' en el imaginario popular, una clase de benchmark o un estándar dorado que inspirará a matemáticos por muchas generaciones.
REFERENCIAS
[1] Registro de record Guinness de 1980 en el área de matemáticas, publicado en math.ucds.edu
[2] How Many Atoms Are There in the Universe? publicado en universetoday.com
[3] Información de la compañía Google, información recuperada desde web.archive.org
[4] Kasner, Edward; Newman, James Roy (1940). Mathematics and the Imagination. Penguin.
[5] Claude Shannon (1950). Programming a Computer for Playing Chess. Philosophical Magazine 41 (314).
[6] Victor Allis (1994). Searching for Solutions in Games and Artificial Intelligence (PDF). Ph.D. Thesis, University of Limburg, Maastricht, The Netherlands. ISBN 90-900748-8-0. Disponible para su descarga aquí.
[7] R. Graham, B. Rothschild, J.H. Spencer, Ramsey Theory, John Wiley and Sons, NY (1990).
[8] Sbiis Saibian(s/f). One to Infinity: A Guide to the Finite. Section 3.2.9 "Graham's Number". Libro web disponible aquí.
[9] Kerr Josh (s/f). Black Cat. Blog. Entrada: "TREE(3) is a big number, I mean really big", disponible aquí.
Nota: la imagen de portada es de: pixelstalk.net
¡Felicitaciones!
Puedes consultar el reporte diario de curación visitando @entropia
Una información bastante agradable he informativa. la matemática es la ciencia que mueve el mundo en el sentido numérico. :D
Muy buena publicación.
Así es!
Interesante tema, gracias por compartirlo.