PRINCIPIOS Y APLICACIONES DE LOS MÉTODOS DE DIFRACCIÓN DE RAYOS X: SOLUCIONES SÓLIDAS SUSTITUCIONALES (I)

Reciban un cordial saludo miembros de la comunidad Steemit. Soy químico, y desde hace diez años estoy trabajando en el área de cristalografía; preparando, montando, midiendo y analizando muestras policristalinas por difracción de rayos X. En el transcurso de mi vida profesional he analizado muestras de semiconductores, minerales, arcillas, catalizadores, carbones activados, nanocompuestos, entre otros.

A partir de una serie de post, quisiera compartir mi experiencia en el área de difracción de rayos X con ustedes. Quiero contarles acerca de los principios y aplicaciones de los métodos en difracción de rayos X: la generación de los rayos X, la parte instrumental de un difractómetro, los portamuestras empleados, los tipos de montaje, la toma y tratamiento de datos, análisis cualitativo y cuantitativo, determinación de parámetros de celda, los programas especializados empleados, entre otros aspectos.

Mi primera experiencia con la técnica fue a partir de la síntesis y caracterización por difracción de rayos X de una solución sólida sustitucional del material sólido Fe2-2xMn2xGe Se4 con composiciones X = 0.5, 0.6 y 0.7 (donde el Fe paulatinamente es reemplazado por el Mn, pasando de una estructura Fe2GeSe4 a MnGeSe4, cuando X = 0 ó X = 1, respectivamente) perteneciente a la familia de compuestos semiconductores del tipo II2IVVI4.

Este trabajo se compone de dos partes fundamentalmente: 1. La síntesis del material semiconductor (Fe2-2xMn2xGe Se4 con composiciones X = 0.5, 0.6 y 0.7), teniendo en cuenta la teoría de soluciones sólidas sustitucional, y 2. La caracterización por DRX (análisis cualitativo, refinamiento de parámetros de celda y determinación del grupo espacial) de las tres composiciones. En tal sentido, en el presente post les quiero hablar de la primera parte y en un segundo post le hablare de la segunda parte.

PRIMERA PARTE

Soluciones sólidas

En un cristal perfecto todos los átomos de la estructura deberían estar en sus posiciones correctas de la red. Esta situación sólo puede existir a la temperatura del cero absoluto, 0 grados Kelvin. Por encima de 0 grados Kelvin aparecen los defectos en la estructura. Estos defectos pueden ser de dos tipos principales: defectos intrínsecos, inherentes al cristal (no cambia la composición total y por ello también se conocen como defectos estequiométricos); y defectos extrínsecos, que se crean cuando un átomo extraño se inserta dentro de la red, el sólido así formado es un compuesto no estequiométrico porque la relación de los componentes atómicos ya no es un número entero simple, (Smart, 1995).

La mayoría de los minerales no son sustancias puras, sino que presentan una composición química variable. Esto es debido a las frecuentes sustituciones de determinados iones o grupos iónicos que presentan semejante radio iónico (diferencias < 15 %) y de carga eléctrica (por ejemplo, Mg+2 por el Fe+2, en posiciones octaédricas o el Al+3 por el Si+4 en posiciones tetraédricas, etc.). En los últimos ejemplos para que se mantenga la neutralidad eléctrica de la estructura deben tener lugar otras sustituciones adicionales. Como resultado de estas sustituciones se producen las soluciones sólidas en las que, en una estructura aparecen dos o más elementos distintos con posibilidad de ocupar en distintas proporciones una misma posición atómica. Aunque el término solución se asocia comúnmente con líquidos y se define como una mezcla homogénea (que presenta una sola fase) entre el componente mayoritario (solvente) y otro que está en menor proporción (soluto), con los sólidos puede darse una situación similar.

Por solución sólida queremos decir que los constituyentes están atómicamente dispersos, algunos de los lugares están ocupados por una clase de átomos y los demás por átomos de la otra clase. No es un compuesto en el sentido estricto, ya que las soluciones sólidas pueden existir generalmente con una composición ampliamente variable, mientras que los compuestos químicos poseen composición constante (Christy, 1971). Existen límites de solubilidad en las soluciones sólidas pero hay excepciones importantes a esta regla, por ejemplo: las soluciones sólidas de cobre y níquel y las de plata y oro. El cobre disuelve cualquier cantidad de níquel que se le añada y viceversa. Lo mismo sucede con las soluciones sólidas de plata y oro. Ejemplos en los cuales existe límite se presentan en las soluciones sólidas de cobre en plata o plata en cobre, el cobre disuelve un máximo de un 8% de plata, y este último metal disuelve un máximo de 8.8% de cobre. En general, mientras más distintos sean los componentes, tanto desde el punto de vista químico como por lo que respecta al tamaño atómico o molecular, más restringida será la solubilidad parcial (Keyser, 1972).

Existen diferentes tipos se soluciones sólidas:

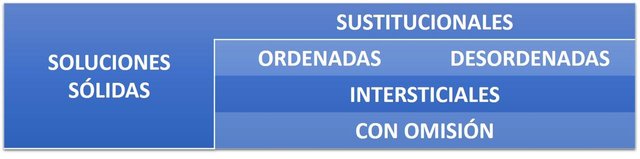
Elaboración Propia

Soluciones sólidas sustitucionales.

Ley de Vegard (Polonio, 1981). Se produce una sustitución de un elemento por otro en todo el intervalo de composiciones posibles determinado por las composiciones de dos miembros extremos. Un buen ejemplo de este tipo de soluciones es el que forma la serie isomorfa del olivino, (Mg,Fe)2SiO4. (uned.es). En el olivino, el Mg+2.puede ser reemplazado parcial o totalmente por el Fe+2 constituyendo una solución sólida completa entre los dos términos extremos forsterita (Mg2SiO4) - fayalita (Fe2SiO4). Otro ejemplo es el que forman los carbonatos de la serie rodocrosita MnCO3 – siderita FeCO3. Pero también existen las sustituciones aniónicas como por ejemplo la formada por la solución sólida completa KCl-KBr, en la que los aniones Cl- y Br- se sustituyen entre ellos.

La solución sólida sustitucional se origina siempre que los átomos de un metal A se alojan en la red cristalina de otro metal B, sustituyéndolo en las posiciones o coordenadas cristalográficas que éste ocupa en la misma. Generalmente, esta sustitución se realiza de una forma fortuita o desordenada, es decir, sin que el soluto A, se sitúe en posiciones sistemáticamente privilegiados de la red cristalina del disolvente B.

Este tipo de disolución sólida se produce entre los elementos con similares volúmenes atómicos. La miscibilidad o capacidad de intercambio de un átomo por otro en función de la temperatura, puede llegar a ser del 100%, en cuyo caso la solución sólida es Isomorfa o continúa. En un sistema isomorfo solamente se encuentra un único tipo de estructura cristalina, sean cuales sean las proporciones de los componentes.

En este caso las estructuras cristalinas de los metales A y B han de ser necesariamente iguales y sus diámetros atómicos relativos (factor de tamaño) no pueden diferir en más del 15 % aproximadamente, debiendo cumplirse además, ciertas condiciones en los estados de valencia de los metales. En el intervalo de concentraciones donde la solución sólida es continua, no se originan cambios de fases o estructuras intermedias; la única modificación que experimenta la red cristalina básica es una ligera variación en el valor de sus parámetros cristalográficos, en función de las diferencias existentes entre los radios atómicos y de las concentraciones relativas del disolvente y del soluto. Si el radio de B es mayor que el de A, el volumen de la celda de este último aumenta con la concentración de aquel y viceversa, siempre que no existan circunstancias particulares que modifiquen las características de los enlaces interatómicos.

La correspondiente variación de los valores de los parámetros de la celda en función de la composición atómica porcentual, es casi lineal en los sistemas binarios de una sola fase de tipo sustitucional homogénea, sobre todo en las redes iónicas o metálicas de tipo cúbico, como pone de manifiesto la ley de Vegard. Pero en general, todos los sistemas muestran desviaciones más o menos conocidas respecto al comportamiento teórico; en la mayoría de los casos estas desviaciones tienden hacia la dirección de la concentración de la red.

La Ley de Vegard proporciona un método bastante directo para determinar teóricamente la composición de una solución sólida es continua o no; para ello basta con medir precisamente un parámetro de la celda unidad y referirlo a una curva de calibración en la cual la abscisa es el porcentaje del átomo sustituido y la ordenada es el valor en Anstromgs del parámetro a de la celda unidad, (Polonio, 1981).

Síntesis de las soluciones sólidas sustitucionales

Para la síntesis de las diferentes composiciones (X = 0.5, 0.6 y 0.7), se utilizaron elementos puros de Magnesio (Mn), Hierro (Fe), Germanio (Ge) y Selenio (Se). Se pesó la cantidad necesaria para completar un gramo para cada una de las diferentes composiciones. En la siguiente tabla se describen los elementos utilizados y las cantidades empleadas para cada una de las síntesis.

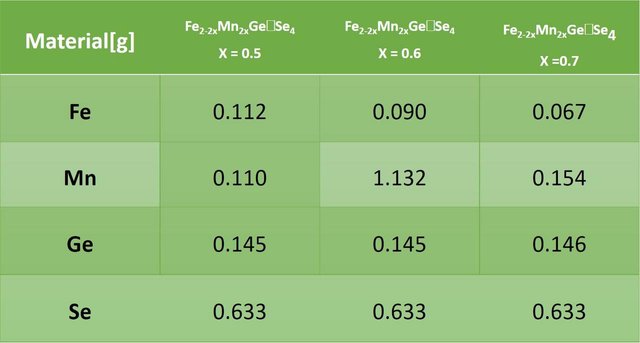
Elaboración Propia

Para realizar la síntesis de las diferentes composiciones (X = 0.5, 0.6 y 0.7) del material Fe2-2xMn2xGeSe4 se utilizó un horno de una zona. El horno fue elaborado por el personal del Laboratorio de Investigación en Materia Condensada de la Escuela de Física de la UIS.

REFERENCIAS

SMART, L y MOORE, E. Química del estado sólido : Una introducción. Wilmintong, Delaware, E.U.A : Adison-Wesley Iberoamericana, 1995. P. 101-169.

CHRISTY, Robert W. Estructura de la materia : Una introducción a la física moderna. Barcelona : Reverte, 1971. p 238.
KEYSER, Carl A. Ciencia de materiales para Ingeniería. Mexico : Limusa-Willey, 1972. p 140.

POLONIO Bermudez. Joaquín. Métodos de difracción de rayos X : Principios y aplicaciones. Madrid : Pirámide, 1981. 461p.

Hasta este punto les he presentado que es una solución sólida y una solución sólida sustitucional, ya que el primera parte de esta investigación consistió en la preparación de tres soluciones sólidas sustitucionales:

Con X = 0.5 se tiene FeMnGeSe4
Con X = 0.6 se tiene Fe0.8Mn1.2GeSe4
Con X = 0.7 se tiene Fe0.6Mn1.4GeSe4

En un siguiente post, le hablare de la manera como se puede realizar el análisis cualitativo por DRX, determinación de parámetros de celda, programas especializados para realizar el refinamiento de estos parámetros y finalmente determinación de grupo especial.

Hasta una próxima oportunidad, les agradezco mucho por la atención que puedan prestar a este post.

Me despido muy cordialmente @cuarzo05.