Estudio del Cálculo: Funciones reales. Parte II
Introducción
En esta oportunidad voy a dar continuidad a la serie del estudio del cálculo: funciones reales. Parte II. En este caso explicare:
- La gráfica de una función.
- Clasificación de funciones.
- Funciones pares e impares.
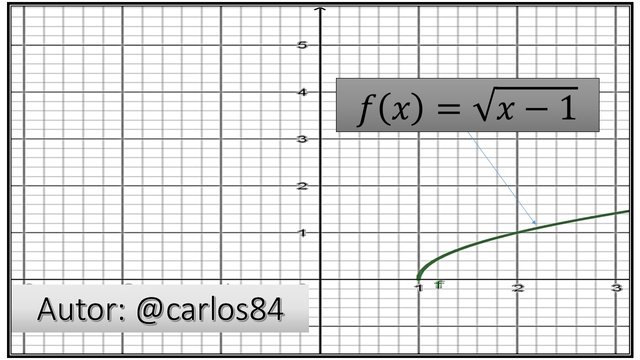
En el post anterior: Estudio del Cálculo: Funciones reales. Parte I, se abordó lo referente a: función, dominio y rango de una función, gráfica de una función tomando en cuenta el criterio geométrico de la recta vertical para saber si una ecuación representa una función real o no. En esta publicación se ampliará otros conceptos fundamentales con los cuales se cerrara la parte concerniente a funciones reales.
Existen otros tipos de evaluaciones que se pueden hacer con las funciones reales, como por ejemplo los criterios crecimiento y decrecimiento de una función real, asíntotas de una función racional, criterios de concavidad, extremos de una función (puntos máximos y puntos mínimos). Todo este estudio se puede efectuar en esta parte pero de una forma empírica, ya que no es sino con el criterio de la primera y segunda derivada que se puede completar todo el estudio respectivo, es por ello que todo este estudio se explicará a cabalidad en la publicación correspondiente de las aplicaciones de la derivada.
Con esta publicación se dará cierre a la serie estudio del cálculo: funciones reales. Quedando abierta para la próxima publicación la continuidad del estudio del cálculo, pero en esta ocasión será la serie que tratara de límite de una función de variable real.

Gráfica de una función
Recordando el criterio geométrico de la recta vertical para poder definir si una ecuación es función o no, debemos saber que esta recta solo debe cortar al gráfico máximo en un solo punto, esto lo que significa que para cada elemento del dominio (números reales en el eje X) solo le debe corresponder un solo elemento del contradominio (números reales en el eje Y). Ya una vez que estemos afianzados en saber que la ecuación es una función, sea que lo sepamos antes o después de graficado en el plano, es donde podremos realizar el estudio respectivo de dominio, rango y criterios de paridad.
Existen dos metodologías a mi entender para poder realizar el gráfico de una ecuación a mano, es decir sin la ayuda de graficador computarizado, estas son las siguientes:
- Si no conocemos el comportamiento básico de la función que pretendemos graficar: si desconocemos qué forma pueda tener la gráfica de determinada función real, lo más idóneo sería construir una tabla de valores donde podamos expresar las imágenes de la función (f(x)) cuando x toma valores arbitrarios. Generalmente los valores arbitrarios de x que aconsejo tomar son: 0,1,-1,2,-2. Si por alguna circunstancia con estos valores todavía no logramos saber que comportamiento toma la función, entonces los podemos ampliar un poco más, quizás pueda ser para x= {3,-3, 4,-4}. Un ejemplo para conseguir imágenes puede ser:
Encuentre las imágenes necesarias para la función 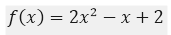
Para ello vamos a probar dándole valores arbitrarios a x de {0,1,-1,2,-2}, para esos valores de x cuando los introducimos en la ecuación de la función obtendremos un f(x) para cada x arbitrario propuesto, por lo que la tabla quedaría de la siguiente manera:

El problema aquí se presenta es debido a que para los valores propuestos de x, no hemos conseguido una imagen f(x)=0, lo que implica que con esos valores de x no hemos obtenido el corte con el eje x. Lo idóneo para este caso es hacer f(x)=0, lo que implica que 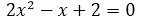 , esto representa una ecuación de segundo grado igualada a cero, por lo tanto hay que encontrar las raíces o valores de x que anulan la ecuación, como la ecuación es de segundo grado, obtendremos dos soluciones, es decir un valor de
, esto representa una ecuación de segundo grado igualada a cero, por lo tanto hay que encontrar las raíces o valores de x que anulan la ecuación, como la ecuación es de segundo grado, obtendremos dos soluciones, es decir un valor de 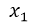 y
y 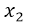 . Para ello es conveniente aplicar la ecuación de la resolvente:
. Para ello es conveniente aplicar la ecuación de la resolvente:
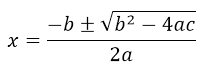 , donde para la ecuación:
, donde para la ecuación: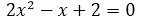 . a=2; b=-1; c=2.
. a=2; b=-1; c=2.
Si hacemos la sustitución de los valores a, b y c, nos quedaría:
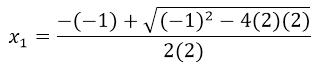 =
= 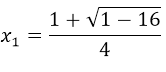 ⇒
⇒
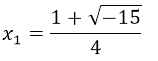
En el resultado podemos ver que dentro de la raíz cuadrada nos está quedando un valor negativo, y como la raíz cuadrada de un número negativo no nos arroja un resultado real, implica que tanto para 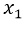 y
y 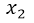 no existe solución real, lo que significa que la ecuación
no existe solución real, lo que significa que la ecuación 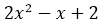 no tiene solución real, y que la gráfica de la función cuadrática no tiene cortes reales con el eje x en el sistema cartesiano.
no tiene solución real, y que la gráfica de la función cuadrática no tiene cortes reales con el eje x en el sistema cartesiano.
La importancia de habernos planteados encontrar f(x)=0 por aparte es que concluimos rápidamente que no existe ningún valor de x para los cuales f(x)=0, con esto limitamos el trabajo de seguir dando valores arbitrarios a x en la tabla de valores.
- Si conocemos el comportamiento de la gráfica de la función: si nos dan la ecuación de una función, y tenemos el indicio de saber cuál es el comportamiento gráfico, entonces es recomendable aplicar la metodología de intersección con los ejes coordenados cartesianos. La intersección con los ejes coordenados se da mediante dos tipos de puntos solución útiles al representar gráficamente una ecuación, estos son en los que la coordenada x o y es cero. Tales puntos se denominan intersecciones con los ejes porque son los puntos en que la gráfica corta (hace intersección con) el eje x o con el eje y. Un punto del tipo (a,0) es una intersección con el eje x de la gráfica de una ecuación si es un punto solución de ésta. Para determinar las intersecciones en el eje x de una gráfica, se iguala f(x)=0 para luego despejar x de la ecuación resultante. De manera análoga, un punto del tipo (0,b) es una intersección con el eje y de la gráfica de la ecuación que representa la función si es un punto solución de la misma. Para encontrar la intersección con el eje y se iguala la x a cero y se despeja la variable y= f(x) de la ecuación resultante.
Cabe recalcar que esta metodología de encontrar los puntos intersección con los ejes cartesianos, no solamente aplica para funciones reales, sino también para cualquier tipo de ecuación que se pueda representar gráficamente en el plano bidimensional (plano cartesiano).
Para aplicar la metodología de puntos intersección con los ejes cartesianos, tomaremos el siguiente ejemplo:
Encontrar los puntos de intersección con los ejes coordenados de la gráfica cuya función es 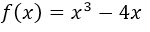
- Para determinar las intersecciones con el eje x, hacemos f(x)=0; y despejamos x.
⇒ 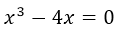 ; como del lado izquierdo de la igualdad tenemos como elemento común la x, entonces sacamos factor común x.
; como del lado izquierdo de la igualdad tenemos como elemento común la x, entonces sacamos factor común x.
⇒ 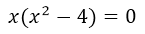 ; la x que tenemos fuera del paréntesis como factor común es nuestra primera solución de la ecuación de tercer grado.
; la x que tenemos fuera del paréntesis como factor común es nuestra primera solución de la ecuación de tercer grado.
⇒ 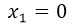
Para conseguir las dos soluciones restantes, tomamos la ecuación que quedo dentro del paréntesis y la igualamos a cero y despejamos la x.
⇒ 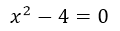
⇒ 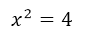
⇒ 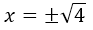
⇒ 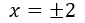
Ya tenemos las tres soluciones que representan los tres cortes con el eje de las x, que serían: 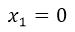 ;
;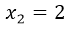 ;
; 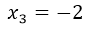 .
.
Estas tres soluciones de la ecuación resultaron de igualar a f(x)=0, por lo que los puntos resultantes en el plano cartesiano de coordenadas (x,y) son:
(0,0); (2,0); (-2,0)
- Para encontrar las intersecciones con el eje y, igualamos la x a cero.
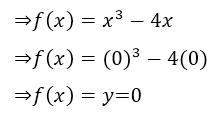
Existen ciertas particularidades gráficas que tiene esta función cúbica que no se pueden cubrir con el criterio de intersecciones con los ejes cartesianos, ni tampoco encontrando las imágenes f(x) para valores arbitrarios de x, estas particularidades son los de poder determinar los puntos máximos y mínimos de la función 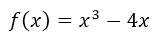 , ya que para conseguir esos extremos relativos hay que aplicar el criterio de la primera derivada, y eso es motivo de otra publicación.
, ya que para conseguir esos extremos relativos hay que aplicar el criterio de la primera derivada, y eso es motivo de otra publicación.
Clasificación de funciones
La noción moderna conocida en la actualidad de función es fruto de los esfuerzos de muchos matemáticos de los siglos XVII y XVIII. Tiempos que en la actualidad, hace de que matemáticos como Leonhard Euler tengamos que atribuirle una mención especial por deberle la notación y=f(x). Hacia finales del siglo XVIII, los matemáticos y científicos habían llegado a la conclusión de que un gran número de fenómenos de la vida real podían representarse mediante modelos matemáticos, construidos a partir de una colección de funciones denominadas funciones elementales. Estas funciones se dividen en tres categorías:
- Funciones algebraicas (polinómicas, radicales y racionales).
- Funciones Trigonométricas.
- Funciones exponenciales y logarítmicas.
En la presente publicación no se explicaran las funciones: trigonométricas, trigonométricas inversas, exponenciales y logarítmicas, ya que para que no resulte tan extenso el post, las trataré en una publicación posterior en donde trataré con sus gráficas, derivadas e integrales.
Para esta publicación tratare con las funciones algebraicas más conocidas, que son las funciones polinómicas:
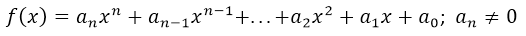
Donde el entero positivo n es el grado de la función polinómica. Las constantes 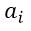 se denominan coeficientes, siendo
se denominan coeficientes, siendo 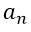 el coeficiente dominante y
el coeficiente dominante y 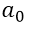 el término constante. En general las funciones polinomiales en sus primeros grados se suelen expresar de la siguiente forma:
el término constante. En general las funciones polinomiales en sus primeros grados se suelen expresar de la siguiente forma:
Grado cero:
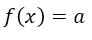
Grado uno:
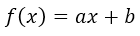
Grado dos:
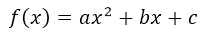
Grado tres:

Criterios de prueba para las funciones pares e impares
- La función y= f(x) es par si f(-x)= f(x)
- La función y= f(x) es impar si f(-x)= -f(x)
Para probar este criterio, y así poder determinar si una función es par o impar, tenemos el siguiente ejemplo: "Determinar si  es par o impar, o ninguna de ambas.
es par o impar, o ninguna de ambas.
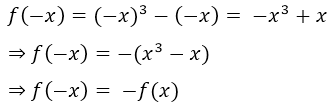
Como cumple con el segundo criterio, podemos decir que la función es impar y al mismo tiempo podemos decir que es simétrica con respecto al origen.
Para poder visualizar el gráfico y ver la simetría con respecto al origen, utilizaremos el software geogebra 5.0 para graficar la función 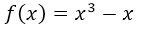 . El gráfico se exportará del software como imagen para ser editado en Microsoft PowerPoint:
. El gráfico se exportará del software como imagen para ser editado en Microsoft PowerPoint:
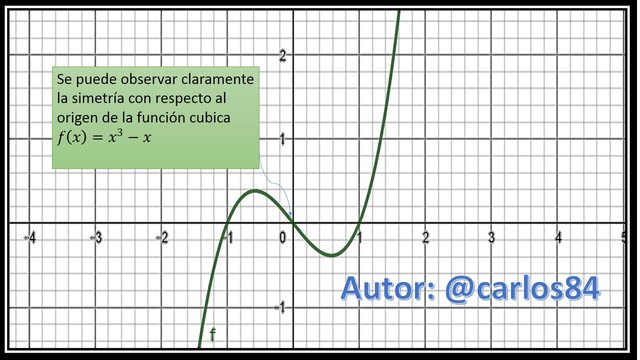
Conclusión y consideraciones
Una vez alcanzado el nivel de aprendizaje óptimo de las funciones reales, debemos de estar capaces para graficar una función del tipo algebraica, ya sea polinómica o radical. Posteriormente también debemos ser capaces de realizar el estudio respectivo como poder determinar el dominio y rango de la función, estudiar la paridad y los criterios de simetría.
Cuando ya se logre explicar las aplicaciones que tiene la derivada con el trazado de curvas, lograremos definir todos los parámetros presentes al momento de graficar una función, sin embargo los principios dados en la primera y segunda parte de la serie "Estudio del Cálculo referente a las funciones reales siembran las bases sólidas para el trazado de las funciones algebraicas más conocidas.

Para complementar esta publicación quiero dar a conocer un video de mi autoría donde se explica el gráfico, dominio y rango de la función 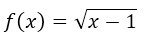
Bibliografía consultada
Cálculo con Geometría analítica. Autor: Ron Larson y Robert P. Hostetler. 8va edición. Editorial Mc Graw Hill. Volumen I. México 2006
El Cálculo. Autor: Louis Leithold. 7ma edición. Editorial Oxford. México 1998.
Muy importante tu comentario @rbalzan79, gracias por el apoyo. Saludos
Excelente post, amigo, @calor84, me hiciste refrescar un poco la memoria. Hacer gráficos es interesante y para mi en particular resultan relajantes. Mis saludos.
Gracias @lauram por el comentario, me complace haberte ayudado a recordar un poco de las gráficas de funciones reales. Muy pronto estare publicando sobre limite y continuidad. Saludos.
I upvoted your post.
Best regards,
@Council
Posted using https://Steeming.com condenser site.
Saludos @carlos84 , gracias por compartir tus conocimiento en el área del calculo, te felicito en la forma dinámica y académica que abordaste este contenido fascinante
Gracias por comentar @chetoblackmetal. Saludos colega