INTERPOLACIÓN POLINÓMICA PARTE 2 – SPLINE CÚBICO NATURAL, PROPIEDADES Y CÁLCULO A PARTIR DE PUNTOS DADOS
Portada del artículo. Fuente: Elaboración Propia utilizando Microsoft Power Point 2010
Saludos a toda la comunidad de #STEM-ESPANOL, #STEEMSTEM y de Steemit en general, en estos momentos en que el Steem ha experimentado una caída significativa en el precio y se ven pocas publicaciones en Steemit, he decidido escribir este post con el fin de contribuir a mantener viva la ciencia en Steemit.
En un artículo anterior se analizaron las nociones básicas de la interpolación y el proceso de obtención del polinomio interpolador mediante el uso de sistemas de ecuaciones lineales, en el presente artículo se analizará un caso especial de interpolación, específicamente, el referente al uso de Splines, la teoría sobre los Splines fue desarrollado por el matemático Isaac Schoenberg alrededor del año 1940 con la finalidad de interpolar datos con un suavizado de curvas.
INTERPOLACIÓN SEGMENTARIA
Asumamos que en un problema de interpolación tenemos 4 puntos, lo más lógico sería entonces realizar una interpolación de tercer grado según vimos en el artículo anterior. Por ejemplo, si tenemos los siguientes puntos
| x | f(x) |
|---|---|
| 1 | 3 |
| 2 | 4 |
| 6 | 7 |
| 8 | 10 |
Tabla N°1 Puntos utilizados para interpolar.
Y realizamos una interpolación cúbica obtenemos el siguiente resultado:
El polinomio de interpolación es:
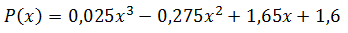
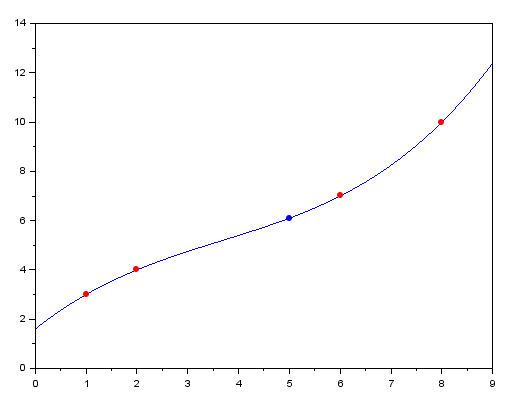
Si usamos dicho polinomio para aproximar el valor de f(x) para x=5 obtenemos f(x)=6,1, este procedimiento se corresponde con la interpolación polinómica tal como se explicó en el artículo anterior, sin embargo, también podemos realizar una interpolación por segmentos, es decir, para los puntos 1 y 2 encontrar un polinomio de interpolación lineal, para los puntos 2 y 3 otro polinomio lineal y para los puntos 3 y 4 un tercer polinomio lineal, en este caso tendríamos una función definida a trozos compuesta por 3 polinomios lineales, dicha función interpola para los 4 puntos dados.
Siguiendo el procedimiento descrito en el artículo anterior, para los 4 puntos mostrados en la tabla N° 1 se obtendrían los siguientes polinomios de interpolación lineal:
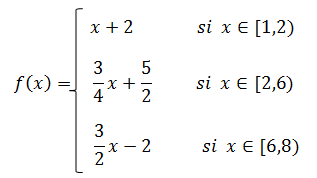
Estos tres polinomios representan la interpolación segmentaria lineal para los cuatro puntos dados, la gráfica de dicha función se representa en la siguiente imagen
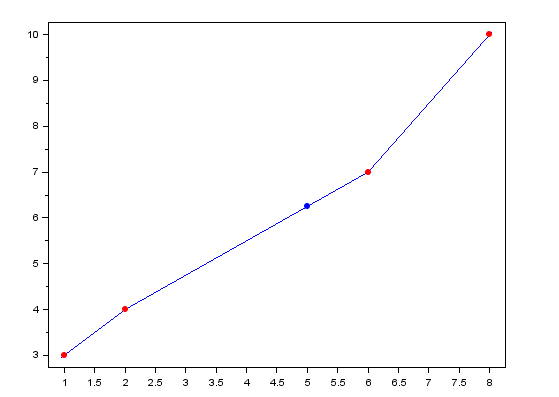
Imagen N° 2. Ejemplo de interpolación segmentaria lineal. Fuente: Elaboración propia utilizando Scilab 5.
Si se desea usar dicha función para aproximar f(5), el resultado sería 6,25.
Sin embargo, la función representada en la imagen N° 2 presenta cambios abruptos en la pendiente en los puntos utilizados para construir la interpolación, si quisiéramos derivar está función nos encontraríamos con el hecho de que en los cuatro puntos iniciales el límite utilizado para calcular la pendiente cambia de valor en ambos lados, debido a esto la función no es diferenciable en dichos puntos.
Con el fin de construir una interpolación segmentaria que sea diferenciable debemos establecer la condición adicional de que los polinomios que se intersectan en los puntos utilizados como base tengan la misma pendiente, es decir, para el ejemplo anterior los polinomios 1 y 2 deben tener la misma pendiente en el punto x=2 y los polinomios 2 y 3 la misma pendiente en el punto x=6.
En la práctica una de las interpolaciones más utilizadas es la interpolación mediante Splines cúbicos. Un Spline se define como una curva diferenciable en cualquier punto que está definida mediante polinomios. Utilizando los puntos de la tabla 1 construiremos el Spline Cúbico correspondiente.
Para los puntos dados construimos polinomios cúbicos que pasen por cada 2 puntos, para los puntos (1,3) y (2,4) obtenemos el primer polinomio
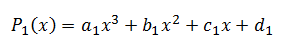
Como pasa por ambos puntos podemos sustituir los valores de x y P(x) de los primeros dos puntos (1,3) y (2,4) obteniendo
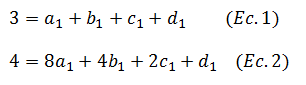
Continuamos con el siguiente par de puntos (2,4) y (6,7)
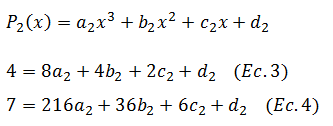
Finalmente para (6,7) y (8,10)
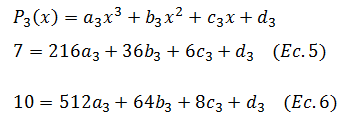
Al encontrar valores que satisfagan estas 6 ecuaciones nos aseguramos de encontrar los tres polinomios cúbicos que pasen por los puntos dados, para asegurarnos que los polinomios que se intersectan tengan la misma pendiente (y el spline sea diferenciable) en dicho punto, observamos en la gráfica que los polinomios 1 y 2 se intersectan en x=2, como la pendiente de dichos polinomios viene dada por la primera derivada se debe cumplir que
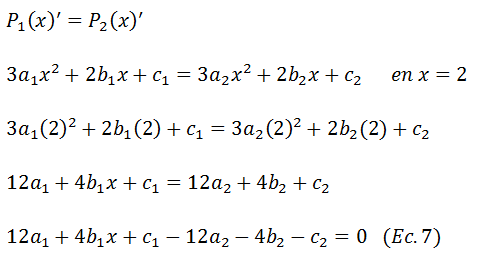
Los polinomios 2 y 3 se intersectan en x=6, como la pendiente de dichos polinomios viene dada por la primera derivada se debe cumplir que
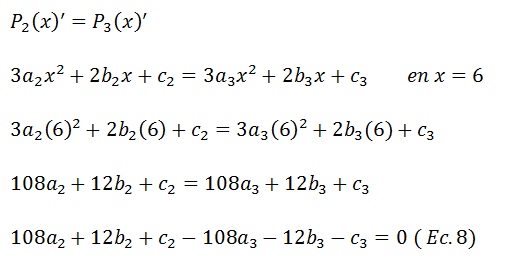
Las ecuaciones 7 y 8 aseguran que los polinomios tengan la misma pendiente, adicionalmente, es conveniente también que tengan la misma concavidad recordando que la concavidad viene dada por la segunda derivada, los polinomios 1 y 2 se intersectan en x=2 luego
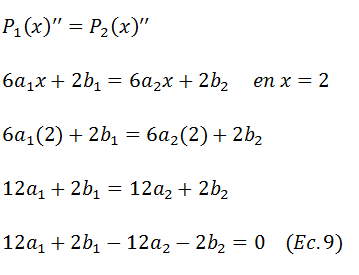
Los polinomios 2 y 3 se intersectan en x=6 luego
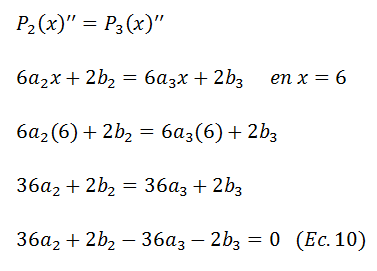
Obteniendo un sistema de ecuaciones lineales de 10 ecuaciones con 12 incógnitas, debido a que el número de incógnitas es mayor que el número de ecuaciones, el sistema es compatible indeterminado, es decir, tiene infinitas soluciones para lograr que tenga una única solución se debe añadir una restricción al spline la cual es la que lo definirá como un spline cúbico natural.
Un Spline cúbico natural es un Spline cúbico en el cual la segunda derivada de los polinomios que pasan por ambos extremos es igual a cero, es decir
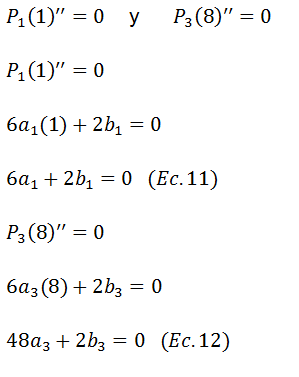
Obtenidas las ecuaciones 11 y 12 unificamos todas las ecuaciones en un solo sistema:
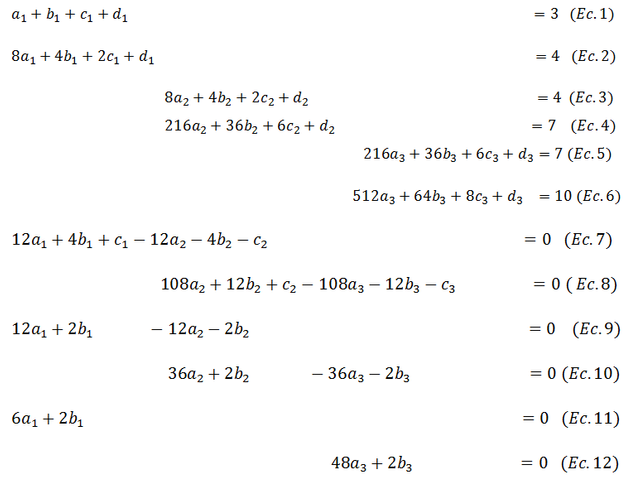
Resolvemos este sistema de ecuaciones lineales de 12 incógnitas utilizando Maxima, mediante el siguiente código:
linsolve([a1+b1+c1+d1=3, 8*a1+4*b1+2*c1+d1=4, 8*a2+4*b2+2*c2+d2=4, 216*a2+36*b2+6*c2+d2=7, 216*a3+36*b3+6*c3+d3=7, 512*a3+64*b3+8*c3+d3=10, 12*a1+4*b1+c1-12*a2-4*b2-c2=0, 108*a2+12*b2+c2-108*a3-12*b3-c3=0, 12*a1+2*b1-12*a2-2*b2=0, 36*a2+2*b2-36*a3-2*b3=0, 6*a1+2*b1=0, 48*a3+2*b3=0], [a1,b1,c1,d1,a2,b2,c2,d2,a3,b3,c3,d3]);
Obteniendo la siguiente solución:
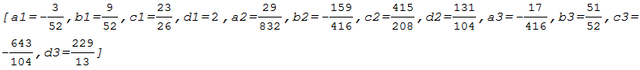
En base a dicha solución construimos el Spline Cúbico Natural:
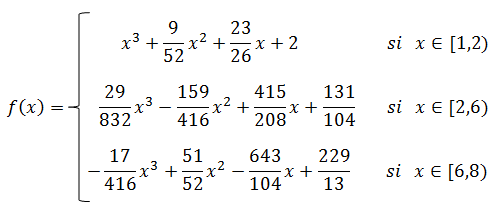
Estos tres polinomios permiten interpolar para los puntos dados, obteniendo la siguiente curva
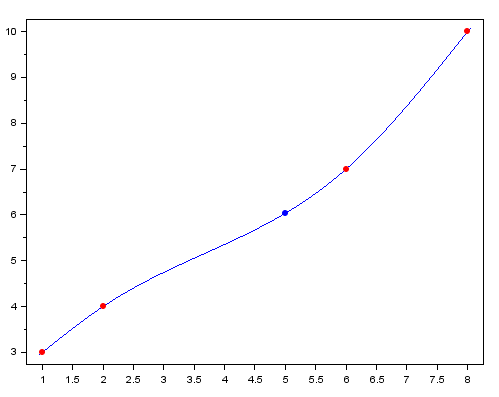
Y un valor de aproximación para f(5) de
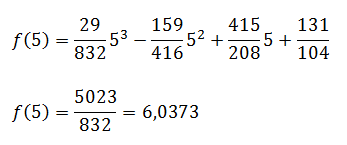
Ahora bien, ¿Que tan cerca está la aproximación por Spline Cúbico Natural a la aproximación mediante la interpolación cúbica?, podemos apreciar ambas gráficas en la siguiente imagen
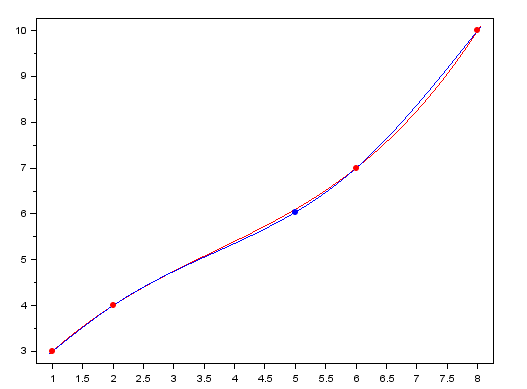
Se puede apreciar que son aproximaciones bastante cercanas, en base a esto el lector podría preguntarse ¿Cuál es la más adecuada?.
El polinomio de interpolación cúbica es más fácil de obtener en cambio los Splines Cúbicos Naturales suelen ser calculados utilizando computadoras, debido a la complejidad de resolver sistemas de ecuaciones lineales de muchas incógnitas (para n puntos el Sistema de Ecuaciones Lineales posee 4n-4 incógnitas).
Otra de las ventajas del uso de Spline Cúbico Natural es que solo requiere polinomios de grado 3, a diferencia de la interpolación polinómica que requiere de un polinomio de grado n-1 para n puntos. Cuando se interpola con polinomios de grado elevado se generan oscilaciones indeseables en la gráfica de la curva obtenida.
Debido a la facilidad de cálculo de los Splines a nivel computacional, son muy utilizados en programas y juegos particularmente en el diseño de los gráficos por ordenador.
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editorial Limusa Willey.
Budnick (2007), Matemáticas aplicadas para administración, economía y ciencias sociales. 4ta edición Editorial Mc Graw Hill.
González (2019), INTERPOLACIÓN POLINÓMICA PARTE 1 – NOCIONES BÁSICAS Y APLICACIÓN EN LA APROXIMACIÓN DE INTEGRALES DEFINIDAS CON ANTIDERIVADAS DESCONOCIDAS (CASO DE ESTUDIO: FUNCIÓN ERROR) STEM-ESPANOL 2019.
Saenz (2009), Cálculo Integral con Funciones Trascendentes Tempranas para Ciencias e Ingeniería. 2da edición Editorial Hipotenusa.
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.
Si deseas leer contenido científico de calidad en habla hispana te invito a revisar la etiqueta #STEM-ESPANOL donde podrás encontrar diversidad de temas, Matemática, Ingeniería, Física, Química, Biología, Medicina, Ciencia, Tecnología y mucho más.

Logotipo del Área de Matemáticas de #STEM-ESPANOL
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Thanks for having used the steemstem.io app. You got a stronger support!
Hi @ydavgonzalez!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV