Conjuntos Numéricos parte III: Los Números Racionales (Q) , una aproximación desde la teoría de cuerpos
Representación gráfica de las fracciones, fuente: @ydavgonzalez
Saludos a toda la comunidad de Steemit, en especial a las comunidades científicas de #STEEMSTEM y #STEM-ESPANOL en estos tiempos de cambio en Steemit me parece oportuno seguir publicando con el propósito de enriquecer el acervo de publicaciones científicas en nuestra querida red social.
En esta ocasión ahondaremos en el conjunto numérico de los racionales, los cuales son números que permiten expresar porciones o partes de un todo, por ejemplo la mitad de una torta o la cuarta parte de una pizza.
Como se planteó en artículos anterior los números naturales surgieron de la necesidad del ser humano de enumerar los elementos que lo rodeaban, mientras que los números enteros permitieron expresar deudas y pérdidas, sin embargo, pronto se hizo evidente para los matemáticos de la antigüedad que necesitaban otro tipo de números con los cuales expresar las partes de un todo, por ejemplo si dividían el pan en varias porciones como podrían representar estas porciones en relación al todo.
La respuesta a esta necesidad surgió con el concepto de las fracciones o números racionales, los cuales se definen como el cociente de dos números enteros, es decir:
“Un número racional es un número de la forma p/q donde p y q pertenecen al conjunto de los números enteros y q es diferente de cero”
De esta forma tenemos los siguientes ejemplos de fracciones
Gráficamente las fracciones suelen representarse de la siguiente forma
Representación gráfica de las fracciones, fuente: @ydavgonzalez
En la imagen anterior se aprecia la región sombreada la cual representa una parte de 4 partes totales, es decir un cuarto (¼)
El conjunto de los números racionales (también llamados comúnmente fracciones) se denota por Q (haciendo alusión a la palabra inglesa Quotient), es evidente que este conjunto es infinito, este conjunto representa un gran avance sobre los enteros debido a que es cerrado bajo las cuatro operaciones de la aritmética lo cual implica que la adición, sustracción, multiplicación y división de dos números racionales siempre nos dará un número racional.
Al igual que con los naturales y enteros la adición, y multiplicación de números racionales cumplen las propiedades conmutativas y asociativas, es decir:
- El orden de los factores no altera el producto a+b=b+a y ab=ba
- Cuando se realiza la operación con tres números no es necesario agruparlos de cierta manera, a+(b+c)=(a+b)+c
Operaciones aritméticas en los números racionales:
1.Adición de fracciones
2.Sustracción de fracciones
3.Multiplicación de fracciones
4.División de fracciones
Fracciones Propias e impropias / Reducibles e Irreducibles
En líneas generales se suelen emplear fracciones en las cuales el numerador sea menor que el denominador (conocidas como fracciones propias), esta convención se debe a que todas las fracciones propias son menores que la unidad en cambio si se trata de una fracción en la cual el numerador toma mayor valor que el denominador estaríamos hablando de una fracción impropia la cual fácilmente puede convertirse a un número entero sumado con una fracción propia, por ejemplo;
La última expresión es lo que se conoce como fracción mixta la cual es equivalente a la fracción impropia original. Si bien a simple vista podemos determinar cuándo una fracción es propia o impropia, no es tan fácil determinar si podemos reducirla, por convención las fracciones se suelen expresar en la forma más reducida posible para lo cual debemos encontrar un número que divida tanto al numerador como al denominador, por ejemplo podemos ver la equivalencia de todas las siguientes fracciones
Todas las fracciones mostradas anteriormente representan al mismo número, sin embargo es la última 2/3 la que no puede reducirse más, en este caso estamos hablando de una fracción irreducible, al lector le puede parecer algo bastante fácil, sin embargo puede determinar si la siguiente fracción es irreducible
Como se puede apreciar no siempre es tan fácil resolver este tipo de problemas, para hacerlos tendríamos que descomponer en factores primos tanto el numerador como el denominador
Con lo cual se demuestra que no es irreducible
Nociones de la teoría de cuerpos aplicadas a los números racionales
En esta sección estableceremos al conjunto numérico de los racionales como un cuerpo matemático para lo cual iniciaremos definiendo el concepto matemático de cuerpo.
En la teoría algebraica de números se define el concepto de cuerpo como un conjunto K en el cual existen dos operaciones internas (+ y *) que cumplen las siguientes propiedades
1)El conjunto K es cerrado para ambas operaciones, es decir se cumple que
2)Las dos operaciones internas son asociativas
3)Las dos operaciones internas son conmutativas
4)Las dos operaciones internas poseen elemento neutro
5)Ambas operaciones tienen un elemento inverso, es decir para todo elemento del cuerpo se puede aplicar cualquiera de las operaciones internas con otro elemento inverso también perteneciente al cuerpo obteniendo como resultado el elemento neutro respectivo.
6)Distributividad de la segunda operación respecto a la primera operación interna
Llegado este punto, es fácil deducir que los números racionales forman un cuerpo debido a que cumplen las propiedades anteriormente enumeradas, sin embargo, si quisiéramos resolver ecuaciones polinómicas dentro de dicho cuerpo no podríamos, por lo tanto tendríamos que recurrir al concepto algebraico de extensión de un cuerpo el cual se relaciona con conjuntos más amplios que se utilizan en la teoría de ecuaciones algebraicas y que se estarán abordando en los próximos artículos
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Budnick (2007), Matemáticas aplicadas para administración, economía y ciencias sociales. 4ta edición Editorial Mc Graw Hill.
González (2020), CONJUNTOS NUMÉRICOS PARTE I: Números Naturales, una Aplicación en Criptografía.
González (2020), CONJUNTOS NUMÉRICOS PARTE II: Los Números Enteros, un enfoque desde la Teoría de Grupos.
Si deseas leer contenido científico de calidad en habla hispana te invito a revisar la etiqueta #STEM-ESPANOL donde podrás encontrar diversidad de temas, Matemática, Ingeniería, Física, Química, Biología, Medicina, Ciencia, Tecnología y mucho más.

Logotipo del Área de Matemáticas de #STEM-ESPANOL

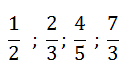
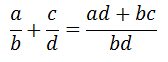
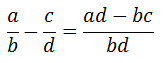
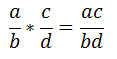
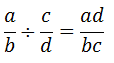
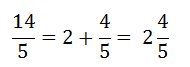
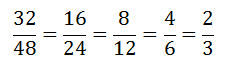
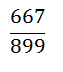
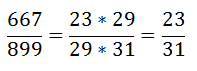

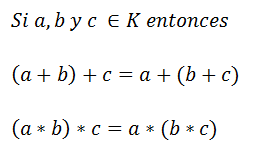
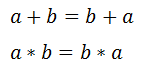
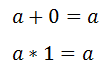
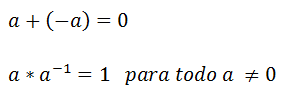
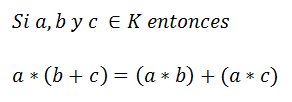
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM. Note that using the steemstem.io app could have yielded an even more important support.