Pi Day 2018 - Pi Music
I woke up this morning and wanted to post this light hearted and fun article fitting with Pi Day. Then I read about the death of Stephen Hawking and wasn't so sure about whether or not to post it. I had a coffee and a bit of thinking. Considering the life Stephen Hawking lead, how devoted he was to science and his sense of humour, I think he wouldn't have wanted to be the reason for a light hearted sciency article to not be published. So I ask you to take a few moments to remember this bright-as-day scientist, this fighter and this inspiration to many a scientist and take a few deep breaths.
Now that we are calm let's try not to be too sad. After all, energy cannot be destroyed, it can only be converted. In whatever state and wherever it may be, I am certain Stephen Hawkings energy is currently working wonders.
Pi Day
Today, the 14th of March, or if you prefer the wonky format 03/14, is international Pi Day. Our fellow Steemian @humanduck and I have created a little project for this occasion. But first some Pi facts.

Image Source
What is Pi?
Pi, or as it is properly written "π", is the sixteenth lowercase letter of the Greek alphabet. In mathematics it represents the ratio of a circle's circumference to its diameter. A circle with a diameter of exactly 1 cm will have a circumference of exactly π cm, or roughly 3.14159 cm.1
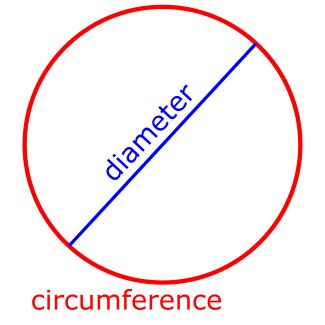
Why is it only roughly 3.14159? Because π is an irrational number. This means that it cannot be represented as a fraction (or ratio) of two whole numbers. No matter which whole numbers you chose, you will never exactly reach π when dividing one by the other. As a result if you try to write down π you will end up with a number that has infinitely many digits that never repeat.
Does π contain everything?
You often hear something like "π is irrational, it has an infinite amount of never repeating digits, so it contains every combination of digits" then they often go on to this mythical idea of π thus containing the date of every persons death and the end of the world and so on. However I was not able to find proof for this.
The statement "it has infinitely many, never repeating digits" is certainly not sufficient to prove that π contains every combination of digits. Take this constructed sequence of digits as an example: Take the digit 1 write it once, now write a 2, now write two 1es, now a 2, now three 1es and so on.
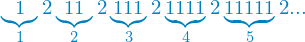
This sequence is clearly infinite and non-repeating. At the same time it clearly does not contain every combination of digits, we only used the digits 1 and 2 after all. As a result the property of "it has an infinite amount of never repeating digits" is insufficient to prove that it contains every combination. It is likely that you will find any given combination of digits within π, but unproven that π contains every combination of digits.
If you know of another property of π that proves that it contains every combination please leave a comment, I would really like to see it proven!

Image Source
What does π contain?
Just some examples I found using this lovely website. You want to find your birth date in π? That's the way to go.
- 03142018 The Death of a legendary Scientist at position 150,741,354
- 14032018 The Death of a legendary Scientist in a more reasonable format at position 184,676,216
- 12345678 at position 186,557,266
- 314159 The first six digits of π (a second time) at position 176,451
- 03101990 German Unity Day at position 44,532,000
- 06041776 USA Independence Day in their wonky format at position 10,417,763
- 04061776 USA Independence Day in a reasonable format at position 11,109,370
Post your favourite sequence and at which position it comes up in π in the comments.
How do you calculate π?
Typically the approach to calculating π is by using an infinite sum. If you take the sum over an infinite amount of summands with certain properties this sum may converge to a fixed value. Here are some examples of how π can be calculated using infinite sums.
The Leibniz formula.2
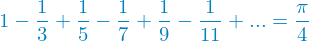
Madhava of Sangamagrama's formular.3
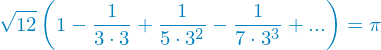
In order to use these sums you typically first have to mathematically analyse them, prove that they do in fact converge towards the desired value and then see how fast they converge. Sadly you can't add infinitely many summands up to get the exact value of π, so you calculate how many summands you need to have a value that is precise to the desired amount of digits.
How did I calculate π?
I calculated π to the 9,000,000,000th (yes, that is the 9 billionth) digit using a well optimized implementation of the Chudnovsky algorithm.4
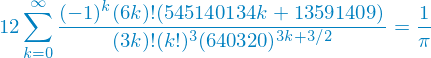
Yes, that is quite the algorithm and I am quite lucky that I did not have to implement this. I found a well optimized implementation by Hanhong Xue. It can be found here. This algorithm is quite hard to implement efficiently but if you manage it, it will converge at a rate of about 13 digits per iteration. This is the fastest converging algorithm I have heard of so far.
The Project
The idea came from @humanduck. He thought "Wouldn't it be fun to generate music from the digits of π?" and I thought "Hell yeah, let's do it!". So I set out to calculate as many digits as I could. I then wrote a little RESTful API to request the digits in a machine readable format. You can in fact use that API yourself if you want, but I will write a post about this later.
While I was working in the backend @humanduck wrote the JavaScript frontend that would use the digits of π to generate music right in your browser.
You can find the result here.
In future we will add a few more tweaks including different modes of generating the music as well as maybe some different instruments.
@humanduck and I are likely to do some more work on this, make it sound a bit better and more varied. So make sure to follow both of us and stay tuned for some more delicious digits.
Stay curious folks.
- The number Pi - https://en.wikipedia.org/wiki/Pi
- The Leibniz' formula - https://en.wikipedia.org/wiki/Leibniz_formula_for_%CF%80
- Madhava of Sangamagrama's formular - https://en.wikipedia.org/wiki/Madhava_of_Sangamagrama
- Chudnovsky Algorithm - https://en.wikipedia.org/wiki/Chudnovsky_algorithm

Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.
CLICK HERE AND VOTE FOR DAVINCI.WITNESS
Deutsche Version hier.
It's quite sad this music. Can you try Fibonacci sequence , please?🙂
I am joking, It's amazing, there is a melody in it!
Armony is everywhere, waiting for us to explore it in any language we're more proficient in.
Great post, interesting community, glad to find you all @davinci.times .