Gardening with Alan Turing, and sketching evolution of plants with Da Vinci - Phyllotaxis
The last published paper of Alan Turing in 1952 promised an upcoming mathematical description of phyllotaxis - the way plants develop and organize their leaves and flower petals. The cyanide laced half eaten apple, however, deprived the world from knowing it's journey from plant to an apple.
The morphogen theory of phyllotaxis, to be described, as already mentioned, in a later paper, will be covered by this computational method. Non-linear equations will be used.
-A. M. TURING, 1952, The Chemical Basis of Morphogenesis1
Top - Alan Turing's statue at Bletchley Park
(Image taken by Jon Callas, CC BY 2.0)
Bottom left - Virtuvian Man by Leonardo da Vinci
(Source, by Janeb13, CC0)
Bottom right - Spiral Phyllotaxis
(Image created by Cayte, CC BY-SA 3.0)
Well, Turing did not make a false promise. He was working on phyllotaxis, but he died before he could publish it. His notes, that were discovered after his death have an elegant mathematical description of how plants organize their organs. His work was later discovered and published by Royal society. You can find archives of his notes here2.
Fibonacci series, plants as mathematicians.
source | Author: Struthious Bandersnatch | CC BY-SA 3.0
In honor of Alan Turing's legacy, people of Manchester and many other people around the world decided to celebrate his 100th birthday. 1000s of sunflowers were grown in this citizen project3. Why, Sunflowers? Because sunflowers show spiral patterning that was described in Turing's incomplete work.
All images taken by @scienceblocks
However, spiral patterning is not unique to sunflowers. The patterning is also observed in how leaves of the plants are organized. Even more interesting is how this patterning happens in Fibonacci arrangement. That is, if you consider the point where first leaf arose as point zero, then the position of second leaf will be, more or less around 137.5 degrees to first leaf. This is fibonacci's or golden angle4.
By @scienceblocks
For those wondering how do we get the golden angle, recall Fibonacci series - 0, 1, 1, 2, 3, ......., ni-2+ni-1. That is, any nth number in series is sum of previous two numbers. Now, take any nth number in the series and find the ratio between this number and the previous number in the series. You will find as you take bigger and bigger n this number converges to 1.6180, commonly known as golden ratio. To find golden angle all you need is to divide a full 360 degree angle in such a way that ratio of the two angles is golden ratio. And this comes out to be 137.5 degrees.
By @scienceblocks
In order to confirm if the angle between two nodes from where leaves arise is indeed around 137.5 degrees, I took a stem from the picture above. I marked two nodes as you can see onthe right. Then I drew an entries circle around it, followed by dividing it into 8 equal parts. The second node fell on 3rd division. So 3/8 of 360 degrees is? 135. Close enough!
Alan Turing and phyllotaxis
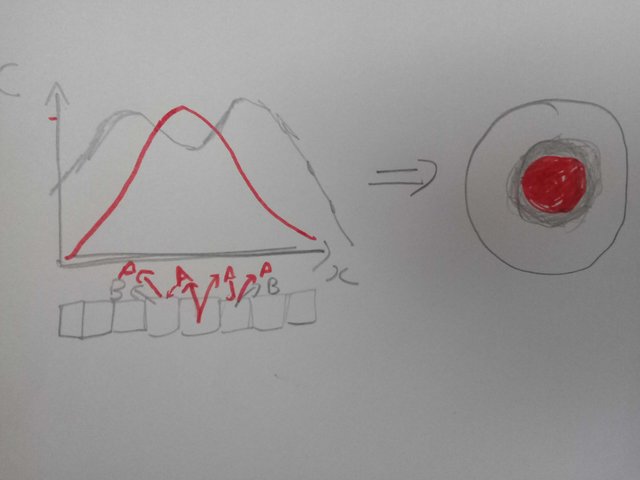
In my previous blog, I discussed how Alan Turing in his 1952 paper, showed the patterning in an embryo. He gave us the idea of morphogens in developmental biology. Morphogens are these signalling molecules, that are secreted by cells, and then act on the neighbouring cells. The response of the cell detecting the morphogen, depends upon where in gradient of morphogen concentration this cell is located. In order to create patterns Turing proposed, that if two or more morphogens act in a activator-inhibitor complex, the gradient of the morphogens will have a pattern. Which means if the effect of morphogen A on a cell is to produce yet another morphogen B, and if B is inhibitor of A, you will see regular patterns.
I explained it in previous blog but just to give you a brief recap, let's say in a sheet of cell the central cell produces A. Let's say response of the other cells is to produce colour red if they sense A. And, if B, the inhibitor of A is produced in response to A, as well, you see red cells surrounded by rings of other colour. Now, put a lot of such sheets in skin and you may get an animal with red spots.
By @scienceblocks(Also used in my previous blog).
To see this mathematically, assume response of the cell to morphogen A is a function of concentration of A.
So, response = Cell(A)
If response is production of B, then concentration of B at any point in space and time will be function of concentration of A. Hence, B = f(A). And if B is inhibitor of A then concentration gradient of A will reduce around high concentration of B.
So if you were working with diffusion of A you can write the equation as following -
Change in concentration of A with time, at a given point in space and time = diffusion coefficient of A*(change in A with distance) + production of A at given concentration of A - destruction of A at given concentration of A(which can be guided by production of B).
This partial differential equation is all you need to predict patterns. However, the sink for A may not always be production of B. It can be consumed by nearby cells, as well. So you don't have to take activator-inhibitor literally. Just think of it as a diffusion + production + destruction equation.
However, this equation is not sufficient to explain the spiral patterning of plants. But then Turing proposed something ingenious in his notes about phyllotaxis. He takes into account how the cell volume and cell membrane properties can effect the diffusion of morphogens itself. So in this case the diffusion coefficient of morphogens is not a constant. He actually took the transport of morphogens into account.
So now, our equation looks like -
Change in A with time, at a given point in space and time = diffusion coefficient of A from cell n to n + 1*(change in A with distance) + production of A at given concentration of A - destruction of A at given concentration of A.
Well in this case you can't use a single equation but you have to model it for every ith and jth cell in the system. You can do this using linear algebra and define cofficients for each ij-th diffusion. All you need then, is to extrapolate this system of equations on a cylinderical geometry, of plant's stem.
Note that, I have avoided using complex equations that were used in actual math behind it all. Well for what I want to say the essence of the math he used serves the purpose. I will probably discuss them in more detail in my future devbio blogs. But, if you are interested in knowing the exact equations do read this paper here5
Was Turing right? The modern understanding.
Based on what we know today, he was very close, I would say. Provided Britain realised how much of contribution to science they are putting at risk, he might have solved what we are still struggling with.(I don't know why it took them 55 years to apologise, but anyway!)
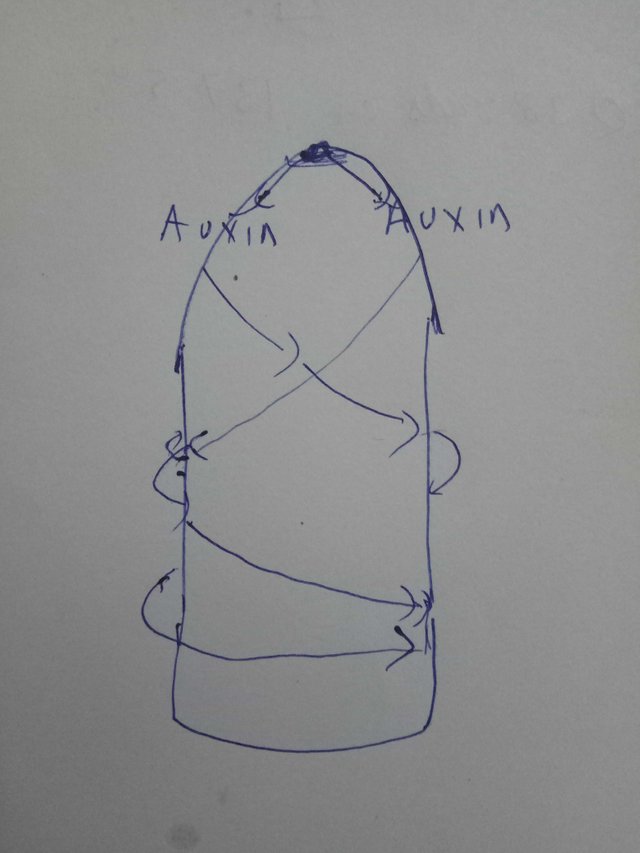
Infact, it was known since 1930s that a plant hormone called Auxin was required for growth of new leaves in the growing apex of the stem. Now, we have discovered that how important this hormone is, in the spiral patterning of organogenesis observed in plants6. So how does this work?
Inspired from Barbara Abraham-Shrauner and Barbara G Pickard, 2011
By @scienceblocks
Don't bother with my rapid bad drawing skills
The top most part of a growing stem is called meristem. The cells in the dome, where the cotyledons are, produce and secrete Auxin, initally. The auxin unlike some other morphogens don't just diffuse in the tissue in conventional way. It is taken by the cells and then transported out to the neighbouring cells and process is repeated. So you can see how close Turing was in his assumption.
But why don't all cells that sense Auxin, start growing a bud, that will grow into leaf? Well, because you need a certain maxima concentration for organogenesis to kick start. So it's not a just a spiral diffusion but also standing waves of auxin gradient are produced to aid pattering. What act as a sink here is the influx of auxin esp at leaf primodia(the place where new bud will form).
So we can already see the components of equation we saw above, starting to fall in place - the diffusion that depends on membrane properties and a sink which act as an inhibitor. However, this alone is not sufficient to explain that why this mechanism produces the divergence angle of 137.5 degrees, between two primodia. A very brilliant solution to this was provided by Barbara Abraham-Shrauner and Barbara G Pickard7. They proposed that two out of phase waves of auxin, arising from the meristem and travelling in opposite direction, can explain the maxima of auxin, that occurs at angles corosponding to the golden angle.
However, the patterning story of auxin is incomplete without the mention of the production term in the equations. The efflux out of cells of auxin at new site is guided and polarized by auxin concentration itself. So auxin not only controls it's appearance at new site it also polarizes the direction of it's own efflux. It achieves this by regulating and polarizing the efflux pumps called PIN18.
Now, Turing in his notes and many other authors after him also discussed that such patterning by auxin should create noisy patterns. It appears that another plant hormone called cytokinin, comes to rescue here. Auxin activates a molecule in cells that inhibit action of cytokinin. This creates another wave of cytokinin activity itself. Since, cytokinin is important for growth of leaves, its action will only maximize in regions where auxin is being depleted - that is after assigning the site for primodia formation9.
So it's not just one but two gradients acting in concert. One that patterns things and another one that buffers the noise. But this still makes me wonder. Why the hell golden angle. I mean it could have done with just random patterning. And this is where the second hero of phyllotaxis, Leonardo Da Vinci comes in.
Evolution of the Golden angle.
By @scienceblocks
Da Vinci did not explain mechanism of phyllotaxis. But he asked why? Why the hell Fibonacci? Even before theory of evolution was formulated by Darwin, Vinci in one of his notebook mentioned that the arrangement of leaves have a functional role. His ideas were also in line with what was suggested by Bonnet in 1700s. According to them this arrangement of leaves at 137.5 degrees maximises the light falling on every leaf. It is the most optimal solution that nature came up with.10.
Nonetheless, some biologists do not like the optimal light explanation. They argue that the leaf surface area and stalk length could accomadate for that. But I think otherwise. I mean it is energetically less costly to organise the leaves in a optimal pattern than play around with size and length. Now obviously, this is not the only arrangement for leaves found in nature. There are patterns that do not follow golden angle rule. So they may have a point. However, the golden angle pattern dominates in terms of abundance.
There is yet another explanation that I like. Which I don't think is mutually exclusive to optimal light hypothesis. This explanation revolves around minimising the energy for plant vasculature network. According to Okabe11, all angles of leaf arrangement observed in nature impinges on minimising the energy cost phyllotaxis, in accordance with optimal interconnectivity of plant transport vessels.
The "why" questions are never really simple to answer. But to me the optimal light hypothesis does make sense. Or maybe I am just biased because Vinci has something to do with it.
What about you? Do you think Vinci was correct? Or do you think there is another evolutionary explanation for patterns of organogenesis in plants. Do share in comments. 1 SBI share for interesting hypothesis.
References.
Signing off
@scienceblocks



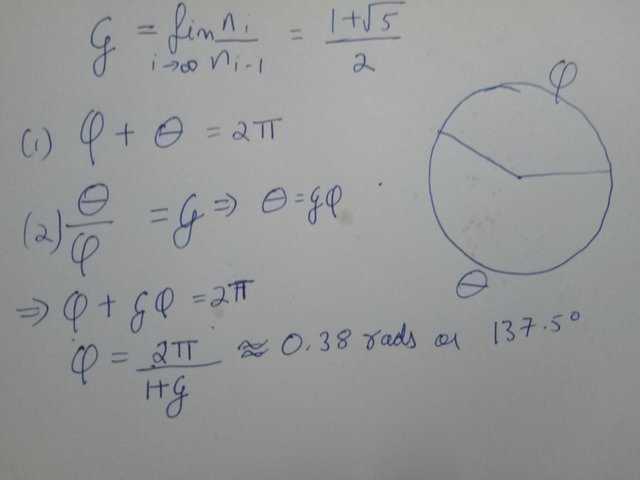



I don't have a full enough grasp of the mathematics to make a sound hypothesis, but this seems very similar in spirit, if not in form, to the advection-diffusion equation we use for modeling chemical transport.
In that case, certain common mathematical constructs pop out not because they are the most efficient, but simply because they tend to always appear when you're working with systems of differential equations. Could that be the case here?
Yeah it's pretty close to it because they are both built up on system of diffusion PDE. And that was mostly the point that of Turing that using these mathematical constructs you can explain the patterns in nature. But as far as efficiency is concerned you are partially right. The patterns are the way they are because the underlying math of PDE is same. However there is another parameter we need to consider when we think of biological systems. They need to maximize their copies - by long survival or high reproduction rate. So all possible patterns that can be made by tweaking components of the equations can compete.
Loved your post and included it in my first attempt to put together posts specifically for biomimicry professionals. You can find it here!
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Congratulations @scienceblocks! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations,
you just received a 18.22% upvote from @steemhq - Community Bot!
Wanna join and receive free upvotes yourself?

Vote for
steemhq.witnesson Steemit or directly on SteemConnect and join the Community Witness.This service was brought to you by SteemHQ.com