The problem of Stinkers deficit in Natchez Native Americam Indian Tribe

Statistics in the service of social sciences
I have recently read the book "Mathematics in modern world", important fact — the year of publication of this book is 1966. At first glance, the title modern may be archaic, but the content of this book says the opposite. It turns out that attempts to model the biological neuron have their origin in those times. The book also contains general problems as examples for the discussed mathematics branches. I did not mention the authors and the concept — this book is a collection of articles from Scientific American, signed with well-known names of the scientific world at that time — although it should be mentioned that we are mainly moving around the mathematical districts. And so the author of the first article is Richard Courant, next names are: Edward Moore, Morris Kline, we also have the physicist Freeman Dyson. In a set containing 11 articles, we have two Poles, which in and of itself proves the level of Polish mathematics. Stanisław Ulam and Marek Kac took up the following issues: artificial intelligence and probability. There are also articles describing the field of mathematics in the physical, biological and social sciences. And on the latter — written by Richard Stone — let's stop for a moment. It is not difficult to guess, social sciences liked the statistics.

And although many mathematicians despise statistics, treating her like a fifth wheel, she still remain under the jurisdiction of the Queen of All Sciences. Although devoid of elegance and imaginative, it has instruments that give us tangible information. Although it lacks theorems and theories that have changed the world, it seems to be so familiar, widely available. Richard Stone takes the case of Natchez tribesmen who once inhabited the Mississippi River System. However, he uses a deeper analysis, not using only dry data. The problem can be reduced to a number-theory-problem which center lies in sequences introducing dependence between the increments of given class groups in subsequent generations.

Marriage system in Natchez Native Americam Indian Tribe
The Indian community was divided into two classes: aristocrats and proletarians. The aristocrats were divided into three subgroups with Suns at the top, lower they were Nobles, and the magnates group were closing Honorable. At the bottom of the social hierarchy were the proletarians called Stinkers. The Natchez tribe had extremely interesting laws regarding marriages, namely: at least one partner in each marriage — husband or wife — must be Stinker. The child born by the mother aristocrat had the rank of mother, but in the case when the mother came from the class of Stinkers and the father had a higher rank — the child inherited the rank by one degree lower. For example: a child born in the father-Stinker and mother-Sun relationship, father-Stinker and mother-Noble, father-Stinker and mother-Honorable, was respectively: the Sun, Noble or Honorable. On the other hand, a child from the mother-Stinker and father-Sun relationship, mother-Stinker and father-Noble, mother-Stinker and father-Honorable were respectively: Noble, Honorable, and Stinker. At the bottom of the social hierarchy, both parents Stinkers had the Stinker offspring.
The Natchez tribe no longer exists, but it remains interesting to analyze the social system defined in such a complex way. It is necessary to create a package of assumptions without which we will not even begin the analysis.
Namely:
- Each member of the Natchez tribe only marries once.
- In each marriage, on average, two children were born: a boy and a girl.
- The amount of the starting population and its distribution to the groups are taken from the literature [1]
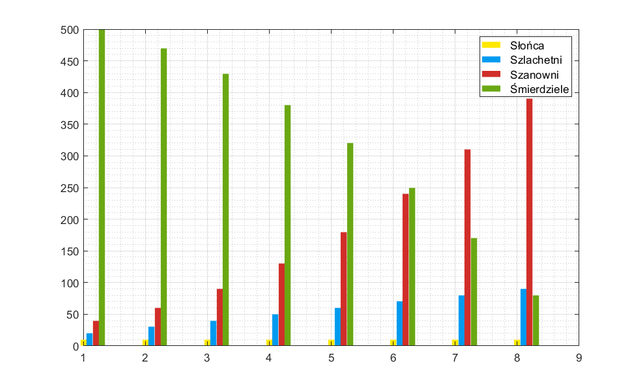
| - | The starting population | I generation | II generation | III generation | IV generation | V generation |
|---|---|---|---|---|---|---|
| Sun (S) | 10 | 10 | 10 | 10 | 10 | 10 |
| Noble (N) | 20 | 30 | 40 | 50 | 60 | 70 |
| Honorable (H) | 40 | 60 | 90 | 130 | 180 | 240 |
| Sum | 70 | 100 | 140 | 190 | 250 | 320 |
| Stinker (R) | 500 | 470 | 430 | 380 | 320 | 250 |
| Sum | 570 | 570 | 570 | 570 | 570 | 570 |
| - | - | - | - | - | - | - |
| - | G | G+1 | G+2 | G+3 | G+4 | G+5 |
| Sun | S | S | S | S | S | S |
| Noble | N | N+S | N+2S | N+3S | N+4S | N+5S |
| Honorable | H | H+N | H+2N+S | H+3N+3S | H+4N+6S | H+5N+10S |
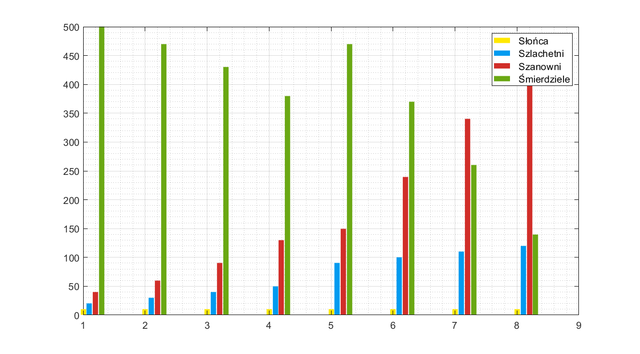
The model — however imperfect — tells us that the Natchez tribe would not survive, functioning in this way, even five generations. There would be no Stinkers. It would then be necessary to introduce modifications into the system of marriages or... kidnapping of Stinkers from neighboring villages. Let's assume that in the fifth generation there was a war in which the Natchez tribe were enriched by prisoners of war, who were converted to Stinkers — 150 people (not including marriages in this generation). The result of the war were also losses in the number of aristocrats, respectively: minus 30 Honorable, and several promotions: plus 30 Nobles.
The graph tells us that the war did not give much. It is possible that the Natchez area has widened, however, the Stinkers class is running out again very quickly. Let us now try to double the initial population of Stinkers — the variant without war.
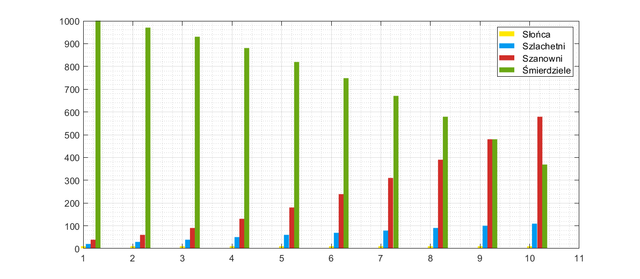
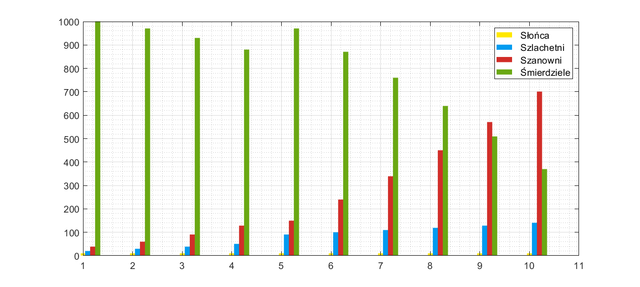
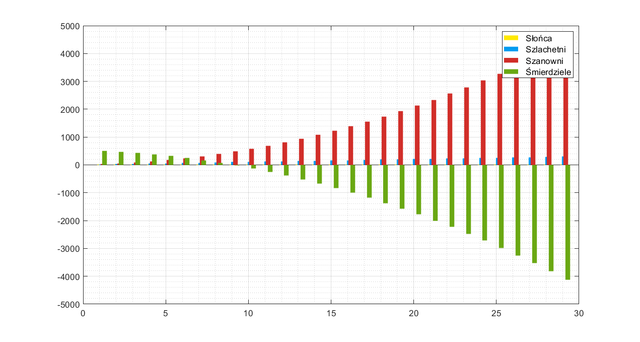
Again, small change. What if we pull simulations on and see 30, 50, 100 generations? The next bars will show us the scale of the Stinkers deficit over the centuries and perhaps this will be the key to maintaining the stability of the system. Below is a chart for the 30 generations.
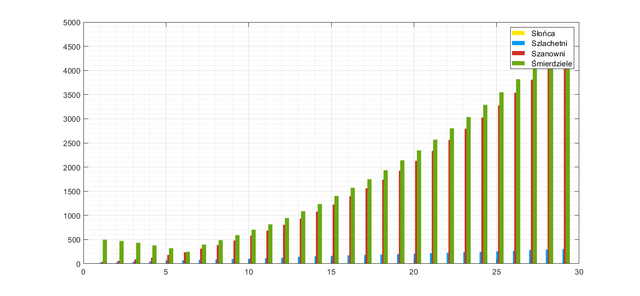
The graph says clearly: the group of Honorable is growing at an alarming rate, which is too fast for any war effort. In addition, the downside is that the Sun population can not grow in the natural way, it is necessary to promote their from the Noble level. The Natchez tribe would have to become a huge empire. Let's try a different approach, let's see how many Stinkers would have to be in the tribe so that the population would function in this system:
The code for this case was written in Matlab and the result in the form of the number of Stinkers in the next generations (assuming that no changes were made to the 5th generation due to the stability of the system):
% Indianie Natchez
NOfGeneration = 30;
S = zeros(NOfGeneration,1);
N = zeros(NOfGeneration,1);
H = zeros(NOfGeneration,1);
R = zeros(NOfGeneration,1);
suma = zeros(NOfGeneration,1);
tab = zeros(NOfGeneration,4);
% Populacja wyjściowa
S(1) = 10;
N(1) = 20;
H(1) = 40;
R(1) = 500;
tab(1:4,1) = [S(1) N(1) H(1) R(1)]';
suma(1) = sum(tab(1:4,1));
%% OPTIMUM
figure
for ii=2:NOfGeneration
if R(ii-1)>(S(ii-1) + N(ii-1) + H(ii-1))
S(ii) = S(ii-1);
N(ii) = N(ii-1) + S(ii);
H(ii) = H(ii-1) + N(ii-1);
R(ii) = R(ii-1) - S(ii-1) - N(ii-1);
tab(1:4,ii) = [S(ii) N(ii) H(ii) R(ii)]';
suma(ii) = sum(tab(1:4,ii));
stem(ii-1,tab(1,ii-1),'LineWidth', 7, 'Color', [1 232/255 0], 'Marker','none')
hold on
stem(ii-1+0.1,tab(2,ii-1),'LineWidth', 7, 'Color', [0 155/255 240/255], 'Marker','none')
hold on
stem(ii-1+0.2,tab(3,ii-1),'LineWidth', 7, 'Color', [209/255 46/255 41/255], 'Marker','none')
hold on
stem(ii-1+0.3,tab(4,ii-1),'LineWidth', 7, 'Color', [106/255 168/255 19/255], 'Marker','none')
hold on
else
S(ii) = S(ii-1);
N(ii) = N(ii-1) + S(ii);
H(ii) = H(ii-1) + N(ii-1);
R(ii) = S(ii) + N(ii) + H(ii);
tab(1:4,ii) = [S(ii) N(ii) H(ii) R(ii)]';
suma(ii) = sum(tab(1:4,ii));
stem(ii-1,tab(1,ii-1),'LineWidth', 7, 'Color', [1 232/255 0], 'Marker','none')
hold on
stem(ii-1+0.1,tab(2,ii-1),'LineWidth', 7, 'Color', [0 155/255 240/255], 'Marker','none')
hold on
stem(ii-1+0.2,tab(3,ii-1),'LineWidth', 7, 'Color', [209/255 46/255 41/255], 'Marker','none')
hold on
stem(ii-1+0.3,tab(4,ii-1),'LineWidth', 7, 'Color', [106/255 168/255 19/255], 'Marker','none')
hold on
end
end
lgd = legend({'Słońca','Szlachetni','Szanowni','Śmierdziele'},'FontSize',13);
set(gca,'FontSize', 13)
grid on
grid minor
R =
500
470
430
380
320
250
400
490
590
700
820
950
1090
1240
1400
1570
1750
1940
2140
2350
2570
2800
3040
3290
3550
3820
4100
4390
4690
5000
Summary
Simulations were quite rigidly outlined, but would the exceptions change drastically presented graphs? I think it's a bit more complicated. There are a few more options to consider, assuming that the Natchez tribe has not complied with its marriage system. Modifications that could have a significant influence on the population — or rather its superposition — are as follows: the possibility of concluding several marriages by the same individual, assuming higher fertility in the class of Stinkers, community reforms degrading the undeserved Honorable (the fastest growing group) to the class of Stinkers, migrations population. Submitting these cases could have an influence on maintaining a good proportion between the aristocracy and the proletariat. Another solution could be the introduction of the middle class and the modification of the marriage system or its complete abolition. Such a solution would inhibit the population's polarization into two groups and bring stability to the tribe's demographics. The middle class could then be the most numerous group (Honorable), which would be an ennoblement for the thriving Stinkers, and at the same time a threat to the lazy Noble and the Sun.
References:
[1] Courant R. i inni — Matematyka w świecie współczesnym, PWN, Warszawa 1966.
[2] Gąssowski J., Łoźny L. — Indianie Ameryki Północnej. Przeszłość i teraźniejszość, Pułtusk 2018 (available online here).
Photos:
[1 — Pixabay]
[2 — FB Negative 1/12 memes]
[3 — Unsplash]



This post has been rated by the user-run curation platform CI! In this platform users are able to manually curate content. This is done regardless of Steem Power, for both rewards and vote size calculation.
Join in at our site here!
https://collectiveintelligence.red/
Or join us on discord to interact with the community!
https://discord.gg/sx6dYxt
This post was submitted for curation by: @anevolvedmonkey
This post was given a rating of: 0.9946015610017322
This post was voted: 82.79%
Upvoted.
Thanks :)
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
I was going to say that this was an interesting evolutionary strategy - a way for aristocrats to avoid too much interbreeding in the future by having to marry stinkers - but then the mathematical treatment upended all that! Interesting and exhilarating!
Mathematical treatment! Yeah, I like it! Thanks a lot @alexander.alexis! :)