Bolyai-Łobaczewski's axiom

Bolyai-Łobaczewski's axiom is the negation of Euclid's fifth postulate and reads as follows:

For given plane P₀ and given straight line L₀ ⊂ P₀ and given point a₀∈P₀—L₀ there exist at least two different straight lines K₁ ⊂ P₀ and K₂ ⊂ P₀ passing through the point a₀ and not crossing straight line L₀.

The full axiomatics of the hyperbolic B-Ł geometry consists of all Euclidian axioms (except fifth) and the above mentioned axiom. This one assumption implies a number of other features of geometry, which in comparison with the geometry we are used to — Euclid's geometry — may seem absurd.

For example, some theorems: in each triangle, the sum of the angles is less than π.

Next, in every convex quadrangle, the sum of the angles is less than 2π (which automatically follows from the previous theorem).

Next, no quadrangle is a rectangle.

Three straight parallel lines on the plane do not need to have the same direction. Here is the illustration of this theorem.

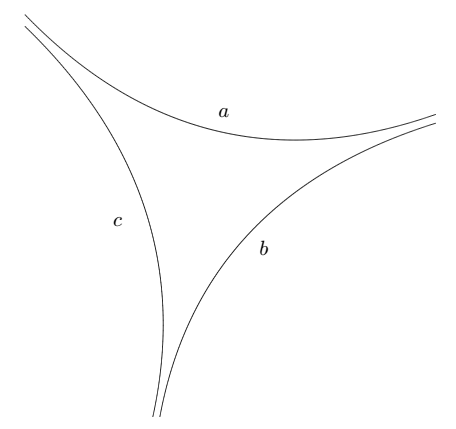
We can also construct a quadrangle with three right angles.

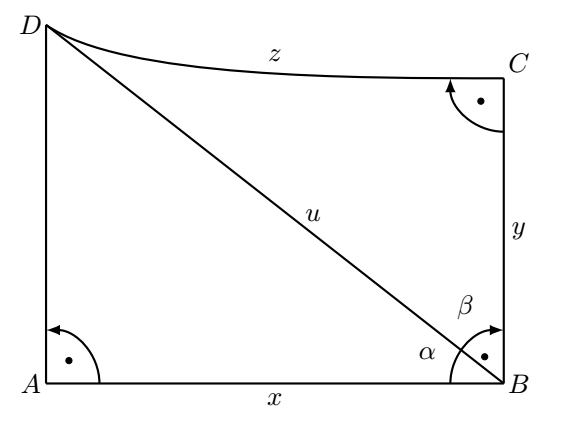
In B-Ł geometry it is necessary to define the angle of parallelism, defect of the polygon and other interesting parameters that help us move around in this space. The Bolyai-Łobaczewski's geometry was initially underestimated, it took time for the scientists to find out the value of this discovery. A point of major importance in this process was Bernhard Riemann's reading "On the Hypotheses which lie at the Bases of Geometry" in which the author went a step further by making deeper generalization. The result was Riemann geometry in which Euclidean and hyperbolic geometry are only special cases.

The Bolyai-Łobaczewski's geometry and reality.

In the previous post (here is the link) was referred to the experiment that Gauss did. Could this experiment work? Imagine the following case: consider a slightly larger triangle, for example a triangle whose vertices are Earth, Sun and Mars. Let this triangle have a sum of angles 179 degrees, so its defect is equal to 1 degree. Let's divide this triangle into triangles of about the size of a triangle examined by Gauss. The distances we study are hundreds of millions of kilimeters and it is easy to calculate that the number of component triangles will exceed one trillion, and thus the defect of a triangle with several dozen kilometers long sides will be about one trillionth degree (about 10^-18 degree)!. It is now clear why Gauss did not notice this defect using measuring instruments.

Measurable defects may occur in astronomy, the largest of the more precisely learned triangles are those that are used to determine the parallax of fixed stars.

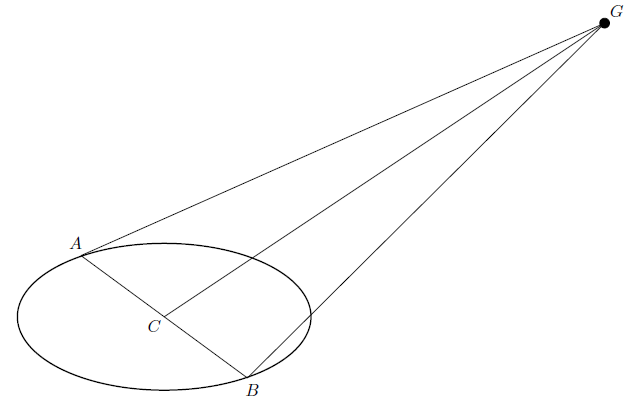
What does the Pythagorean theorem look like in this case? How to calculate the field of this triangle? Maybe another time :)

---

More abour Euclid's fifth postulate in my previous post: Euclidean and non-euclidean geometry

---

All graphics are made in Texmaker. To whom it may concern: here is the code to generate the second graphic:

\documentclass{minimal}
\usepackage{tikz}

\begin{document}
\begin{tikzpicture}

%\draw [help lines] (-10,-6) grid (9,5);
%\draw (0,0) circle (0.5cm);

\draw[thick] (-5,-4) to (1,-4);
\draw[thick] (-5,0.7) to (-5,-4);
\draw[thick] (1,0) to (1,-4);

\draw[thick] (-5,0.7) to (1,-4);


\draw[thick] (1,0) .. controls (-1,0) and (-4,0) .. (-5,0.7);

\draw[>=latex,->,thick] (0.3,-4) arc (180:90:0.7cm);
\draw[>=latex,->,thick] (1,-0.7) arc (270:180:0.7cm);
\draw[>=latex,->,thick] (-4.3,-4) arc (0:90:0.7cm);


\node[thick] (l) at (-5.2,0.7) {$D$};
\node[thick] (l) at (-5.2,-4) {$A$};
\node[thick] (l) at (1.2,-4) {$B$};
\node[thick] (l) at (1.2,0.2) {$C$};
\node[thick] (l) at (-1.5,-1.8) {$u$};
\node[thick] (l) at (1.2,-2) {$y$};
\node[thick] (l) at (-2,0.3) {$z$};
\node[thick] (l) at (-2,-4.2) {$x$};
\node[thick] (l) at (0,-3.6) {$\alpha$};
\node[thick] (l) at (0.5,-3) {$\beta$};


\draw[fill=black] (0.7,-0.3) circle (0.04cm);
\draw[fill=black] (0.75,-3.65) circle (0.04cm);
\draw[fill=black] (-4.7,-3.7) circle (0.04cm);

\end{tikzpicture}
\end{document}

---

References:
[1] Borsuk K., W. Szmielew — Podstawy geometrii, PWN, Warszawa 1970.
[2] Kulczycki S. — Geometria nieeuklidesowa, PWN, Warszawa 1960.