Dynamics of moods
The description of the motion has always fascinated scientists. It began with philosophy and attempts to describe phenomena using words. Then the question arose, is there no better language to describe the motion? The language of mathematics seems to be better in this discipline — the simplest application will be observation of a given body and notation in mathematics. Imagine two monkeys sitting on trees separated from each other. One of the monkeys throws a banana to the other monkey. Suppose we mark a black marker dot on the banana and observe the motion of this dot. We will get an approximate description of the banana motion. Approximate — because it is not strict. Banana can, for example, rotate, and the point is too primitive to reflect this. But this is just a trivial example. Atwood's machine, physical pendulum, beams, plates, membranes — all these objects have been described in detail. What if we want to describe, for example, the motion of the cloud in the sky? How to describe the cloud? As a set of points? As a continuous system? If so, is the density at every point the same or just assume it is the same? And another issue: how, for example, to describe changes in the woman mood? Let's think about it.

I think that if we assume that changes in the woman mood are a periodic function dependent on many factors (eg rain, sun, time, lack of time, wind, lack of wind, cold, heat, orderliness, clutter, season of the year etc.) the problem is solved — each periodic function can be decomposed into a Fourier series. What's more! We do not have an approximate solution, but an analytical solution, thus taking into account all physical phenomena. The problem lies only in the description of the function, which we will decomposing in this series. It is very rare that we have this function explicitly, often we have to accept various simplifications so that calculations are possible at all. Let's assume that the function looks something like this:
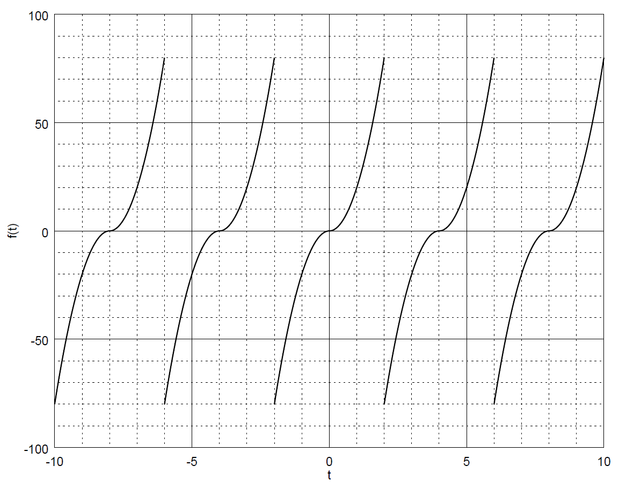
5 periods of the input function.
If we decompose this function into a Fourier series then we will know the frequency of specific harmonics and the mystery of the woman mood will be almost solved. We will get a graph composed of sines, cosines and a constant component. It's a lot of effort to link the result to reality, but I think that the constant component will be something like the intensity of grumbling. The first harmonic would be connected with the processes that affect the woman the most — it's hard to escape before that. However, what should interest us the most is the higher harmonics in the form of various actions, eg raising eyebrow or gesturing. They should be recognized and reduced as soon as possible. It is also worth setting a period of the function and not placing it in any calendar or diary, but from this time the calendar should be subordinated to this graph. Not only the calendar, it is also recommended to adjust the time of the day, and preferably to develop a dedicated mechanism of the watch, which will inform about the upcoming action. A small remark: an attempt to find an analogy between seasons/days of the week will end in a fiasco, and this may lead to brutal disclosure, remember the simplifications we have accepted and that the woman's mood has infinitely many variables. It's best if everything was subordinated to this graph from now on, you'll do well as you put it in your mind. Draw it in high resolution and remember the location of each pixel. Only such methods can give a guarantee of controlling the situation, looking into notes at each harbinger of thunder and the sound of unblocking the gun-lock may turn out to be nervous and troublesome. Sometimes the gun simply misfires and then you do not have to try to reduce the amplitude of the mood. On the contrary — if we take this step, the curve may be tilted in opposite direction (expertly: a change in the harmonic function phase at a time that is not favorable), and then our actions change into the role of forcing the vibrations rather than reducing them. Nobody wants it. It is recommended to take the observer's position and wait for the harbingers of other operations.
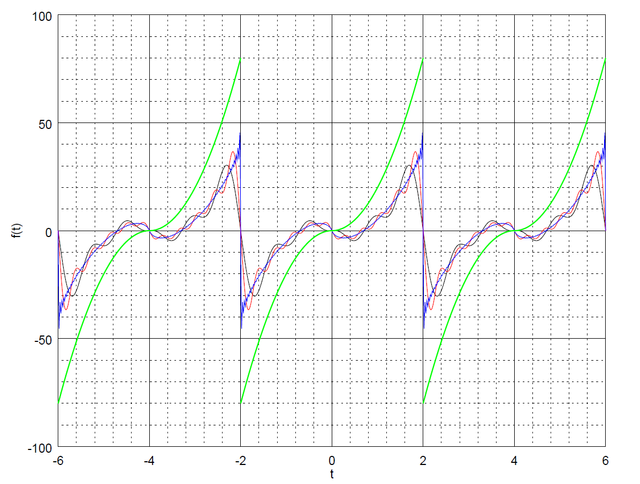
Function decomposed into Fourier series. Colors:
green — the original function
black — the first 5 terms of the Fourier series
red — the first 10 terms of the Fourier series
blue — the first 100 terms of the Fourier series.
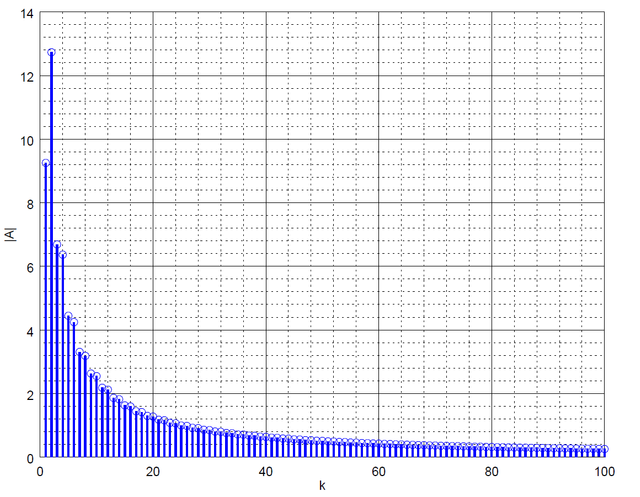
The amplitude spectrum tells us that the first harmonic does not play first fiddle at all, so we have a unique temperament.
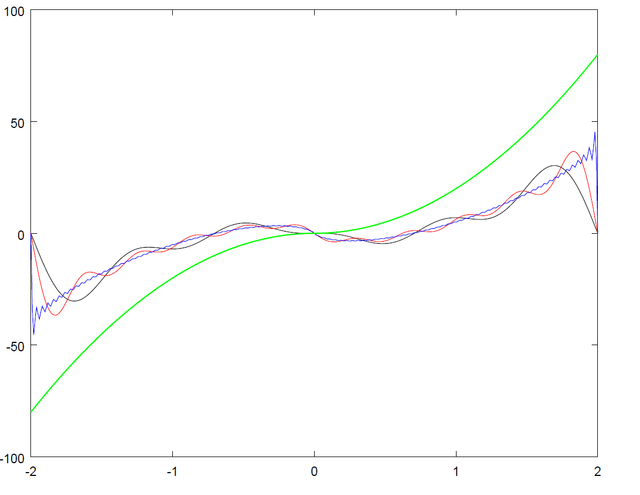
And a zoom of one mood period.
Let me remind you once again — one must remember about the simplifications that cause us to know the behavior of the mystical function of the woman mood and we can describe it in a precise way. As before — the sound of unblocking the gun-lock may be a bad omen this time, it seems that every weapon shoots itself once a year. I think that this is a special case. If we would like to generalize this claim, it would be appropriate to specify that we are not concerned with the period of the year, but with the period of the woman's mood. Then each weapon would shoot in another period of the year, but each time in the period of the function sought. This is explained by such common shooting and bombing, which is not included in the Fourier series. However, the quid pro quo. If we want to build a better model, then a specific subject should be subjected to detailed research and in this way should collect data that would be used to optimize the function. There are, unfortunately, many variables, and this process would consist in recording reactions to stimuli (preferably notes should be made on an illustrative graph and mark the amplitude of deflections with a new variable causing distortion). Notes must be made in secret or saved with a cipher. For this you can use encryption programs, but it is recommended to omit the trivial Caesar code and use the achievements of Polish cryptologists. Do you think that who was the original Enigma model? If we combine the theory-number approach with the algorithm of cryptology, we have a good chance of success that our cipher will remain effective for some time. However, you must constantly remember who is on the other side and who is trying to break the code. After a month, it is worth making a thorough modification in the encryption program.

To sum up, whatch your back, but the drawn graph can be a big support. A small addition: if the described method seems too complicated, I would have two more ideas. The first one concerns the measurement of the speed of mood changes (and thus not the mood itself and its amplitude, but the speed of change). Then it would be appropriate to stock up on a stopwatch and record the average speed after a given (preferably infinitesimal) moment of time. The second idea. Measure the acceleration of mood changes. And at this point, we are introducing an important modification. Measuring the acceleration of mood changes would be highly troublesome. But instead, you can measure the acceleration of the hand or eyebrows, which will be in close correlation with the acceleration of mood. Yes, this is a way out, not forget that the solution will be big approximation, but it will be. The technology comes with the help — we take an accelerometer and glue it on the woman's hand and/or brows. You can use a trick that is a ring and a painless earring. It's good if it was a WiFi connection — it will be easier to collect data and avoid excusing from the cable connected to the ring and earring. In this way, we will register data reflecting the shape of the desired graph. Whenever a woman uses her eyebrows to show her mood change or gesturing, our chart will change shape. Annotation about the hand: you have to suppress the low frequencies that will in relatation to daily duties, the high pass filter will work best. I suggest a digital one to avoid suspicion. The speed chart should be later passed through the integrator (once), and if we measure the acceleration, we integrate it twice. The result will be a function of deflecting mood over time. Good luck!
Photos:
[1] — ArtsyBee, Pixabay
[2] — Tamara Bellis, Unsplash
Here a bit more about the Fourier series.



This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!