Biography of Bernhard Riemann (1826 — 1866)
Georg Friedrich Bernhard Riemann was born on 17 September 1826 in Breselenz in the Principality of Hannover, as the second of six children of rural pastor Friedrich Bernhard Riemann and Charlotte Ebell. Already during Bernhard's initial education, which his father took care of, the boy's abilities in the field of mathematics were revealed very early.

At Easter in 1840, Bernhard left his family home and began studying at the Hannover high school. Two years later his grandmother died and due to this he resigned from high school. This period of his life was difficult because of his innate shyness and longing for his loved ones, which can be seen in his letters. Nevertheless, he gained a solid job and became one of the most urgent and brightest students. After the death of his grandmother, in 1842, pastor Riemann moved his son to a school called Johanneum in the vicinity of the family's home — in Lüneburg. Bernhard continued to receive good grades, the best always in mathematics. His talents in this field were discovered by the headmaster of school. He contributed to the development of the young mind by loaning the student for an independent study of mathematical works, which he absorbed at an amazing pace. As far as we know, Riemann got to know Euler's works from mathematical analysis and Legendre on the theory of numbers.
On April 25, 1846, Bernhard began studying philology and theology at the University of Göttingen. This decision, which was not consistent with the mathematical interests, was influenced perhaps by the hope of finding a job and coming to help the father at work and the willingness to relieve the family in financial problems. But apart from philological and theological lectures he also attended lectures in mathematics. In the winter semester of the academic year 1846/1847 he listened to Gauss lecture on the method of least squares. Riemann recalled this period in his habilitation speech. The propensity for mathematics proved to be too strong, and finally Bernhard obtained permission from his father to give himself completely to his beloved study.At this point, one should stop for a moment over Riemann's relationship to the above-mentioned Gauss. Carl Friedrich Gauss (1711 — 1855 )is called the "Prince of Mathematicians" because of the amount and significance of his discoveries. In the period in which Riemann came to Göttingen, he dealt with problems belonging to applied mathematics. The young student could not expect that he would get the opportunity to get acquainted with the new ideas from this side, all the more that the 70-year-old Gauss was reluctant to lecture without paying attention to the number of listeners. An additional difficulty in contact with the old professor was Bernhard's shyness. No wonder that in 1847 he left Göttingen and joined the University of Berlin. According to F. Klein, it is necessary to call Riemann a Gauss's student, and even more: the only proper student of this mathematician who showed an understanding of his ideas, which results from comparing the scientific heritage of both scientists. Riemann often referred to Gauss, as exemplified by the lecture On the Hypotheses which lie at the Bases of Geometry.
It would take too much time to list the lectures that Riemann attended in Berlin. Let's just mention that he listened to Jacobi and Dirichlet. From the first, he took interest in algebra and theoretical mechanics, and from the second the method of work; illustrating claims by means of clear examples, thorough analysis of the basics and avoidance of long calculations, which method he used in his habilitation lecture.
At Easter 1849, Riemann returns to Göttingen and participates in lectures in natural sciences and philosophy. With particular interest, he listens to lectures by Wilhelm Weber in the field of experimental physics. He also hired Riemann as an assistant in physical exercises. This employment, and the extraordinary care with which Riernann prepared the results of his work for publication, meant that his doctoral thesis Grundlagen für eine allgemeine Theory der Functionen einer veränderlichen complexen Grösse was submitted to the Faculty of Philosophy scarcely in November 1851. This dissertation was very positive assessed by Gauss, who informed the author that he himself has been preparing works for the same subject for years, but he is not limited to it. Public defense of work and doctoral thesis took place on December 16, 1851. From that moment, nothing stood in the way of habilitation.
According to the regulations in force, the candidate for habilitation should have submitted the habilitation dissertation to the Department and present three topics as a proposal for a trial lecture, of which the Department elected one. The postdoctoral thesis was: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe. Riemann suggested the following topics for the test lecture:
1. History of the question about the visibility of functions in the form of trigonometric series.
2. On the solution of two equations: the second degree with two unknowns.
3. On the hypotheses that underlie geometry.
Apart from understandable surprise, the source of the additional difficulty was the fact that he had to give a lecture to members of the Department of Philosophy, and some of them did not have mathematical education. Therefore, to make their research more accessible to them, he skipped all the analytical formulas and derivations in the course of the lecture. Nevertheless, he did so with so much grace that it can be faithfully reproduced. Gauss, who despite the accepted custom chose the third of the presented topics, being curious about how difficult a young scientist will deal with, during the return journey from the Department's office he had the highest appreciation and rare excitement to express to Wilhelm Weber about the depth of Riemann's thoughts .
On February 23, 1855, Gauss died, and Lejeune Dirichlet, who came from Berlin to Göttingen, took his place. He intended to appoint Riemann as an associate professor. This attempt, although it did not bring the expected result, gave at least one positive effect in the form of a small salary set for the young mathematician. It was not until 9 November 1857 that Riemann was appointed an associate professor at the Philosophy Department of the University of Göttingen. It was due to Dirichlet, who from the beginning of his office in this city became interested in Bernhard. After the death of Dirichlet, Riemann was appointed as a full professor in July 1859. This year was a year of great successes for him. In December he was unanimously elected an ordinary member of the Scientific Society in Göttingen. Already earlier, in August, the Berlin Academy of Sciences awarded him the title of correspondent member in the mathematics and physical field.
Unfortunately, in 1862, Riemann he suffered from lungs and the disease was soon to be the cause of his untimely death. He traveled to Italy three times to save his health, but they did not bring much results. During the third of them, Bernhard Riemann died. It was on July 20, 1866, in Selasca on the Lago Maggiore lake.
The activity and scientific achievements of Bernhard Riemann are impressive. They amaze both in terms of spread and the number of problems and topics to be addressed. However, after the death of this scholar, the depth and breadth of his thoughts began to appear. He himself published only a small part of his results. It was probably influenced by the extraordinary care with which he prepared his work for publication. It is not surprising that during his short, only fifteen-year academic career, he published only eleven works. The first of them was the aforementioned doctoral dissertation Grundlagen für eine allgemeine Theories der Functionen einer veränderlichen complexen Grösse, published in 1851. Subsequent works show the extent of Riemann's range of interests. We have dissertations in the field of theoretical physics, in the field of mathematics, concerning: abelian functions, number theory, integral theory, geometry, so-called analysis situs and other issues.
However, the greatest influence of Riemann's output on European mathematical thought began with the posthumous publication of all his works. Among them was a lecture On the Hypotheses which lie at the Bases of Geometry. Feliks Klein, who at that time began his independent scientific work, remembers the extraordinary impression that this lecture had on young mathematicians. This publication entailed a number of others, which, appearing almost immediately after her, took up and further advanced its results. Among them, one can mention the works of such authors as Beltrami, Christoffel and Lipschitz.
References:
[1] Dembek J., Kraków: Życiorys Bernharda Riemanna (Matematyka, Społeczeństwo, Nauczanie) from: R. Dedekind, Bernhard Riemann's Lebenslauf, in: Bernhard Riemann’s gesammelte mathematische Werke, Dover Publications Inc., New York 1953, s. 539-558
Photos:
[1] Bernhard Riemann in 1863
[2] Bernhard Riemann as a student
[3] Friedrich Besemann — University of Göttingen in 1837 (watercolor)
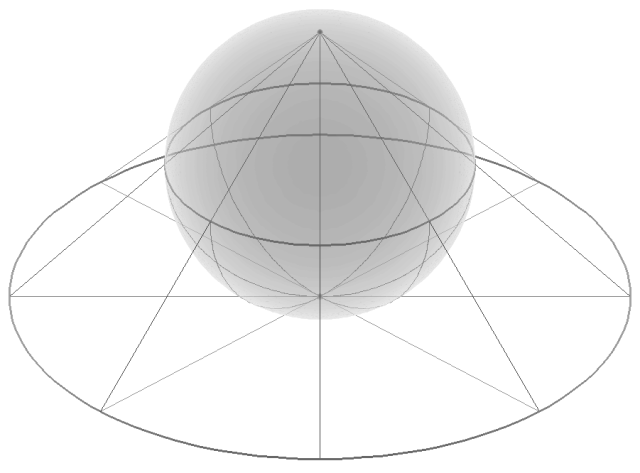
[4] Projecting a sphere to a plane
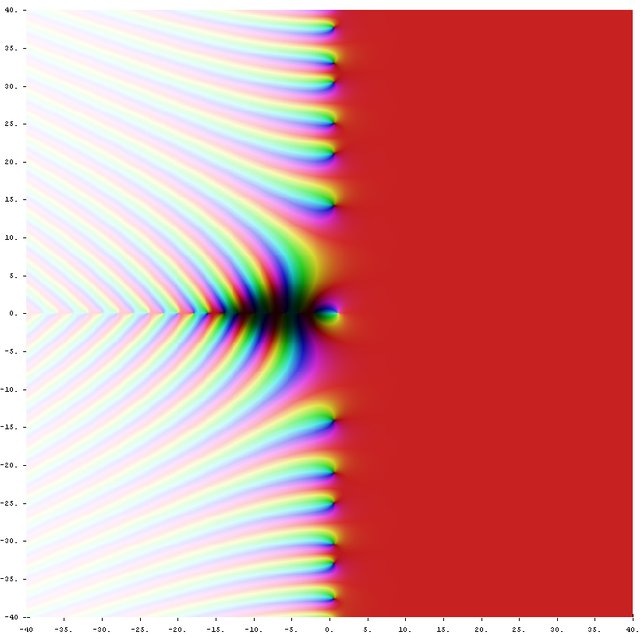
[5] Riemann zeta function in complex plane
[6] Riemann zeta function and its connection with prime numbers; generated in Texmaker




.png)
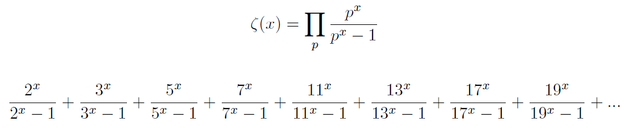
nice post. Some of the photo links are not referencing to the page with the copyright. I will be very happy if you can add those references :)
Done. All photos are in public domain, except for 4th (CC BY-SA 4.0).
Good job.
Do you know Galois? He is one of the few mathematicians who had an action-packed life. Might be nice to write a similar post about him.
Thanks :)
Yes, I heard about Galois. I'm impressed by him, he had a lot of confidence but also great knowledge to take on the problems that he considered at such a young age